Day2 设立计算图并自动计算

Day2 设立计算图并自动计算(给代码截图参考)

1. numpy和pytorch实现梯度下降法
   1.2. 设定初始值
   1.3. 求取梯度
   1.4. 在梯度方向上进行参数的更新
   1.5. numpy和pytorch实现线性回归
2. pytorch实现一个简单的神经网络

a. 实现梯度下降Gradient Descent
原理：训练模型的目的→为了得到合适的w和b→合适的w，b是误差函数的最小值点→沿着误差函数的导数（梯度）下降的方向可找到函数的极小值点（简单的就是该点 ，复杂的后面讨论极小值与最小值点）→梯度下降法来一步步的迭代求解，找到该点

#导包
import torch
#
import torch.nn as nn
import numpy as np
import matplotlib.pyplot as plt

#设置超参数
# Hyper-parameters
input_size = 1
output_size = 1
#训练的次数？
num_epochs = 60
#学习率，相当于步长，太大会振荡，太小会影响效率
learning_rate = 0.001

#训练数据集
# Toy dataset
x_train = np.array([[3.3], [4.4], [5.5], [6.71], [6.93], [4.168], 
                    [9.779], [6.182], [7.59], [2.167], [7.042], 
                    [10.791], [5.313], [7.997], [3.1]], dtype=np.float32)

y_train = np.array([[1.7], [2.76], [2.09], [3.19], [1.694], [1.573], 
                    [3.366], [2.596], [2.53], [1.221], [2.827], 
                    [3.465], [1.65], [2.904], [1.3]], dtype=np.float32)
                    
#线性回归模型的建立
# Linear regression model
model = nn.Linear(input_size, output_size)

#误差函数（损失函数）和初始化
# Loss and optimizer
criterion = nn.MSELoss()
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate)  

#训练模型
# Train the model
for epoch in range(num_epochs):
    # Convert numpy arrays to torch tensors
    inputs = torch.from_numpy(x_train)
    targets = torch.from_numpy(y_train)

    #前向传播
    # Forward pass
    outputs = model(inputs)
    loss = criterion(outputs, targets)
    
    #反向传播和初始化
    # Backward and optimize
  
    optimizer.zero_grad()    #梯度置零
    loss.backward()           
    optimizer.step()
    
    if (epoch+1) % 5 == 0:
        print ('Epoch [{}/{}], Loss: {:.4f}'.format(epoch+1, num_epochs, loss.item()))

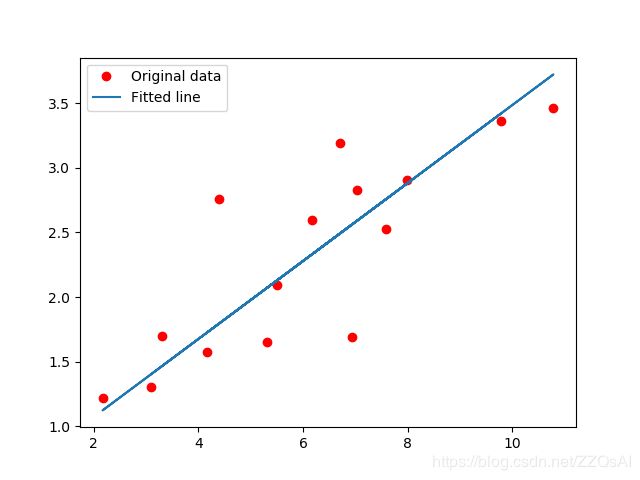
#绘制图像
# Plot the graph
predicted = model(torch.from_numpy(x_train)).detach().numpy()
plt.plot(x_train, y_train, 'ro', label='Original data')    #原始数据
plt.plot(x_train, predicted, label='Fitted line')           #学习到的w和b定义的回归线
plt.legend()
plt.show()

#保存模型检查点
# Save the model checkpoint
torch.save(model.state_dict(), 'model.ckpt')

b.实现一个简单的神经网络

import torch
import torch.nn as nn

class ConvNet(nn.Module):
    def __init__(self):
        super().__init__()
        # 1,28x28
        self.conv1=nn.Conv2d(1,10,5) # 10, 24x24
        self.conv2=nn.Conv2d(10,20,3) # 128, 10x10
        self.fc1 = nn.Linear(20*10*10,500)
        self.fc2 = nn.Linear(500,10)
    def forward(self,x):
        in_size = x.size(0)
        out = self.conv1(x) #24
        out = F.relu(out)
        out = F.max_pool2d(out, 2, 2)  #12
        out = self.conv2(out) #10
        out = F.relu(out)
        out = out.view(in_size,-1)
        out = self.fc1(out)
        out = F.relu(out)
        out = self.fc2(out)
        out = F.log_softmax(out,dim=1)
        return out