矩阵论笔记:约束优化方法之拉格朗日乘子法与KKT条件
| 约束优化方法之拉格朗日乘子法与KKT条件 |
文章目录
- 一、无约束优化
- 二、等式约束优化
- 三、不等式约束优化
- 四、参考文献
在约束最优化问题中,约束条件分为等式约束与不等式约束,对于等式约束的优化问题,可以直接应用拉格朗日乘子法去求取最优值;对于含有不等式约束的优化问题,可以转化为在满足 KKT 约束条件下应用拉格朗日乘子法求解。拉格朗日求得的并不一定是最优解,只有在凸优化的情况下,才能保证得到的是 最优解,所以本文称拉格朗日乘子法得到的为 可行解, 其实就是局部极小值,接下来从无约束优化开始介绍。
一、无约束优化
首先考虑一个不带任何约束的优化问题,对于变量 x ∈ R N x \in \mathbb{R}^N x∈RN 的函数 f ( x ) f(x) f(x) ,无约束优化问题如下: (1) min x f ( x ) \min_x f(x)\tag{1} xminf(x)(1)
根据Fermat(费马定理) 直接找到使目标函数得 0 的点即可 即 ∇ x f ( x ) = 0 \nabla_xf(x) = 0 ∇xf(x)=0,如果没有解析解的话,可以使用梯度下降或牛顿方法等迭代的手段来使 x x x 沿负梯度方向逐步逼近极小值点。
注意:梯度的本意是一个向量(矢量),表示某一函数在该点处的方向导数 沿着该方向取得最大值,即函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大(为该梯度的模)。
二、等式约束优化
当目标函数加上约束条件之后,问题就变成如下形式:
(2) min x f ( x ) s . t . h i ( x ) = 0 , i = 1 , 2 , . . . , m \begin{aligned} &\min_{x } \ f(x) \\ &s.t. \ \ \ h_i(x) = 0 , i = 1,2,...,m \\ \end{aligned} \tag{2} xmin f(x)s.t. hi(x)=0,i=1,2,...,m(2)
约束条件会将解的范围限定在一个可行域,此时不一定能找到使得 ∇ x f ( x ) = 0 \nabla_xf(x)=0 ∇xf(x)=0的点,只需找到在可行域内使得 f ( x ) f(x) f(x)为 最小的值即可,常用的方法即为拉格朗日乘子法,该方法首先引入 Lagrange Multiplier(拉格朗日乘子) α ∈ R m \alpha \in \mathbb{R}^m α∈Rm,构建 Lagrangian 如下:
(3) L ( x , α ) = f ( x ) + ∑ i = 1 m α i h i ( x ) L(x,\alpha) = f(x) + \sum_{i=1}^m \alpha_i h_i(x)\tag{3} L(x,α)=f(x)+i=1∑mαihi(x)(3)
求解方法如下:首先对 Lagrangian 关于 α α α 与 x x x 求偏导数,并且令值为 0 :
(4) { ∇ x L ( x , α ) = 0 ∇ α L ( x , α ) = 0 \left \{ \begin{aligned} \nabla_x L(x,\alpha)= 0 \\ \nabla_{ \alpha } L(x,\alpha)= 0 \end{aligned} \right.\tag{4} {∇xL(x,α)=0∇αL(x,α)=0(4)
求得 x 、 α x 、α x、α 的值后,将 x x x 带入 f ( x ) f(x) f(x) 即为在约束条件 h i ( x ) h_{i}(x) hi(x) 下的可行解,这样做的意义是什么呢? 接下来看一个直观的示例:
- 对于二维情况下的目标函数是 f ( x , y ) f(x,y) f(x,y),在平面中画出 f ( x , y ) f(x,y) f(x,y) 的等高线,如下图的虚线所示:
并只给出一个约束等式 h ( x , y ) = 0 h(x,y)=0 h(x,y)=0 , 如下图的绿线所示,目标函数 f ( x , y ) f(x,y) f(x,y) 与约束 h ( x , y ) = 0 h(x,y)=0 h(x,y)=0 只有三种情况,相交、相切或者没有交集,没交集肯定不是解,只有相交或者相切可能是解,但相交得到的一定不是最优值,因为相交意味着肯定还存在其它的等高线在该条等高线的内部或者外部,使得新的等高线与目标函数的交点的值更大或者更小, - 这就意味着只有等高线与目标函数的曲线相切的时候,才可能得到可行解.
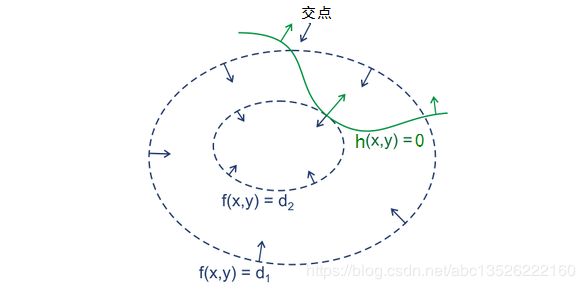
- 因此给出结论:拉格朗日乘子法取得极值的必要条件是目标函数与约束函数相切,这时两者的法向量是平行的,即:
(5) ∇ x f ( x ) – α ∇ x h ( x ) = 0 \nabla _xf(x) – \alpha \nabla_xh(x) = 0\tag{5} ∇xf(x)–α∇xh(x)=0(5)
所以只要满足上述等式,且满足之前的约束 h i ( x ) = 0 , i = 1 , 2 , … , m h_i(x) = 0 , i = 1,2,…,m hi(x)=0,i=1,2,…,m;即可得到解,联立起来,正好得到就是拉格朗日乘子法。这里只是直观展示了一下拉格朗日乘子法的几何推导 ,并没有给出详细的证明。
三、不等式约束优化
当约束加上不等式之后,情况变得更加复杂,首先来看一个简单的情况,给定如下不等式约束问题:
(6) min x f ( x ) s . t . g ( x ) ≤ 0 \begin{aligned} &\min_x \ f(x) \\ & \ s.t. \ \ g(x) \le 0 \end{aligned}\tag{6} xmin f(x) s.t. g(x)≤0(6)
对应的 Lagrangian 与图形分别如下所示:
(7) L ( x , λ ) = f ( x ) + λ g ( x ) L(x, \lambda) = f(x) + \lambda g(x)\tag{7} L(x,λ)=f(x)+λg(x)(7)
这时的可行解必须落在约束区域 g ( x ) g(x) g(x) 之内,下图给出了目标函数的等高线(iso-contours)与约束:
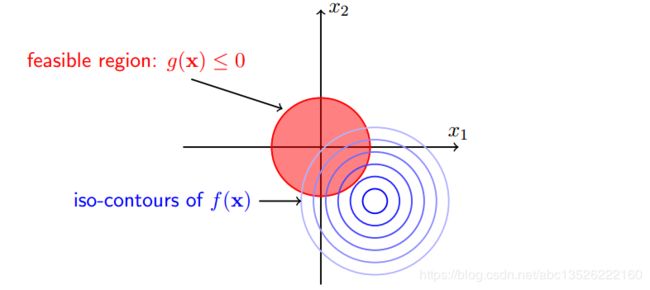
由图可见可行解 x x x 只能在 g ( x ) < 0 g(x)<0 g(x)<0 或者 g ( x ) = 0 g(x)=0 g(x)=0 的区域里取得:
-
当可行解 x x x 落在 g ( x ) < 0 g(x)<0 g(x)<0 的区域内,此时直接极小化 f ( x ) f(x) f(x) 即可;
-
当可行解 x x x 落在 g ( x ) = 0 g(x)=0 g(x)=0 即边界上,此时等价于等式约束优化问题.
-
当约束区域包含目标函数原有的的可行解时,此时加上约束可行解扔落在约束区域内部,对应 g ( x ) < 0 g(x)<0 g(x)<0 的情况,这时约束条件不起作用;
-
当约束区域不包含目标函数原有的可行解时,此时加上约束后可行解落在边界 g ( x ) = 0 g(x)=0 g(x)=0 上。下图分别描述了两种情况,右图表示加上约束可行解会落在约束区域的边界上。
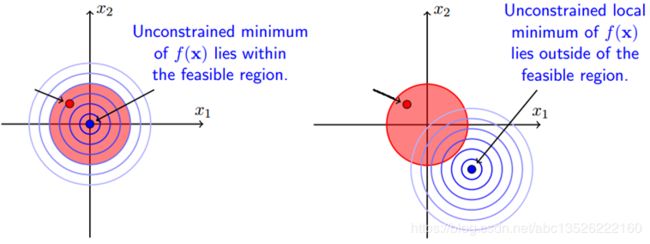
-
以上两种情况就是说,要么可行解落在约束边界上即得 g ( x ) = 0 g(x)=0 g(x)=0(等式约束) ,要么可行解落在约束区域内部,此时约束不起作用,另 λ = 0 λ=0 λ=0 消去约束即可,所以无论哪种情况都会得到:
(8) λ g ( x ) = 0 \lambda g(x) = 0\tag{8} λg(x)=0(8)
还有一个问题是 λ λ λ 的取值,在等式约束优化中,约束函数与目标函数的梯度只要满足平行即可,而在不等式约束中则不然,若 λ ≠ 0 λ≠0 λ̸=0,这便说明 可行解 x x x 是落在约束区域的边界上的,这时可行解应尽量靠近无约束时的解,所以在约束边界上,目标函数的负梯度方向应该远离约束区域朝向无约束时的解,此时正好可得约束函数的梯度方向与目标函数的负梯度方向应相同:
(9) − ∇ x f ( x ) = λ ∇ x g ( x ) -\nabla_x f(x) = \lambda \nabla_xg(x)\tag{9} −∇xf(x)=λ∇xg(x)(9) -
上式需要满足的要求是拉格朗日乘子 λ > 0 λ>0 λ>0 ,这个问题可以举一个形象的例子,假设你去爬山,目标是山顶,但有一个障碍挡住了通向山顶的路,所以只能沿着障碍爬到尽可能靠近山顶的位置,然后望着山顶叹叹气,这里山顶便是目标函数的可行解,障碍便是约束函数的边界,此时的梯度方向一定是指向山顶的,与障碍的梯度同向,下图描述了这种情况 :

可见对于不等式约束,只要满足一定的条件,依然可以使用拉格朗日乘子法解决,这里的条件便是 K K T KKT KKT 条件。接下来给出形式化的 K K T KKT KKT 条件 首先给出形式化的不等式约束优化问题:
(10) min x f ( x ) s . t . h i ( x ) = 0 , i = 1 , 2 , . . . , m g j ( x ) ≤ 0 , j = 1 , 2 , . . . , n \begin{aligned} &\min_x \ f(x) \\ &s.t. \ \ \ h_i(x) = 0 , \ i = 1,2,...,m \ \\ & \ \ \ \ \ \ \ \ \ \ g_j(x) \le 0, \ j = 1,2,...,n \end{aligned}\tag{10} xmin f(x)s.t. hi(x)=0, i=1,2,...,m gj(x)≤0, j=1,2,...,n(10)
列出 Lagrangian 得到无约束优化问题:
(11) L ( x , α , β ) = f ( x ) + ∑ i = 1 m α i h i ( x ) + ∑ j = 1 n β i g i ( x ) L(x,\alpha,\beta) =f(x) + \sum_{i=1}^m \alpha_i h_i(x) + \sum_{j=1}^n\beta_ig_i(x)\tag{11} L(x,α,β)=f(x)+i=1∑mαihi(x)+j=1∑nβigi(x)(11)
经过之前的分析,便得知加上不等式约束后可行解 x x x 需要满足的就是以下的 K K T KKT KKT 条件:5个
(12) ∇ x L ( x , α , β ) = 0 β j g j ( x ) = 0 , j = 1 , 2 , … , n h i ( x ) = 0 , i = 1 , 2 , … , m g j ( x ) ≤ 0 , j = 1 , 2 , … , n β j ≥ 0 , j = 1 , 2 , … , n \begin{aligned} \nabla_{x} L(x, \alpha, \beta) &=0 \\ \beta_{j} g_{j}(x) &=0, j=1,2, \ldots, n \\ h_{i}(x) &=0, i=1,2, \ldots, m \\ g_{j}(x) & \leq 0, j=1,2, \ldots, n \\ \beta_{j} & \geq 0, j=1,2, \ldots, n \end{aligned}\tag{12} ∇xL(x,α,β)βjgj(x)hi(x)gj(x)βj=0=0,j=1,2,…,n=0,i=1,2,…,m≤0,j=1,2,…,n≥0,j=1,2,…,n(12)
-
(1) :拉格朗日取得可行解的必要条件;
-
(2) :这就是以上分析的一个比较有意思的约束,称作松弛互补条件;
-
(3) ∼ (4) :初始的约束条件;
-
(5) :不等式约束的 Lagrange Multiplier 需满足的条件。
主要的 K K T KKT KKT条件便是 (3) 和 (5) ,只要满足这俩个条件便可直接用拉格朗日乘子法, S V M SVM SVM 中的支持向量便是来自于此,需要注意的是 K K T KKT KKT 条件与对偶问题也有很大的联系,下一篇文章就是拉格朗日对偶。
四、参考文献
- http://www.cnblogs.com/ooon/p/5721119.html
- https://blog.csdn.net/xianlingmao/article/details/7919597