POJ1990 MooFest 树状数组 题解(附图)

MooFest

Time Limit: 1000MS		Memory Limit: 30000K
Total Submissions:9207		Accepted: 4167

Description

Every year, Farmer John's N (1 <= N <= 20,000) cows attend "MooFest",a social gathering of cows from around the world. MooFest involves a variety of events including haybale stacking, fence jumping, pin the tail on the farmer, and of course, mooing. When the cows all stand in line for a particular event, they moo so loudly that the roar is practically deafening. After participating in this event year after year, some of the cows have in fact lost a bit of their hearing. 

Each cow i has an associated "hearing" threshold v(i) (in the range 1..20,000). If a cow moos to cow i, she must use a volume of at least v(i) times the distance between the two cows in order to be heard by cow i. If two cows i and j wish to converse, they must speak at a volume level equal to the distance between them times max(v(i),v(j)). 

Suppose each of the N cows is standing in a straight line (each cow at some unique x coordinate in the range 1..20,000), and every pair of cows is carrying on a conversation using the smallest possible volume. 

Compute the sum of all the volumes produced by all N(N-1)/2 pairs of mooing cows. 

Input

* Line 1: A single integer, N 

* Lines 2..N+1: Two integers: the volume threshold and x coordinate for a cow. Line 2 represents the first cow; line 3 represents the second cow; and so on. No two cows will stand at the same location. 

Output

* Line 1: A single line with a single integer that is the sum of all the volumes of the conversing cows. 

Sample Input

4
3 1
2 5
2 6
4 3

Sample Output

57

题意:现在有n头牛,每头有一个听力v和距离x,两头牛之间说活需要的能量为

x[i]代表牛i所在的位置

v[i]代表牛i所需的能量

现在让求;

思路:

    先对牛按照V从小到大排序,这样上式就可以改成;

    而对于,我们可以将牛i之前的所有牛分成两部分:x小于牛i的,x大于牛i

在数轴上表示,就是在i的左边或者右边

    对于i左边的数,我们可以用 (bufw为小于x的距离总和,bufn为x小于牛i的个数),这样用容斥可以求出i左边的绝对值之和

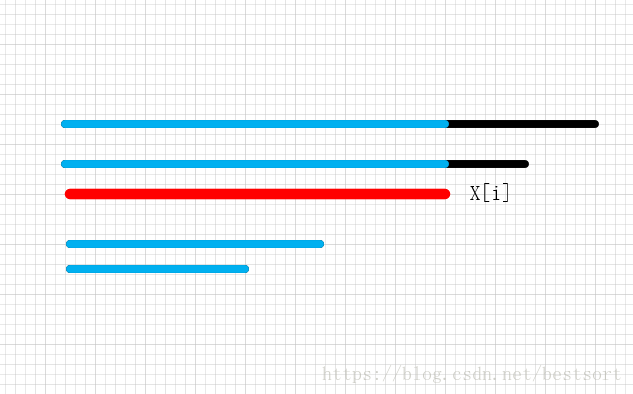
    对于i右边的数,我们用所有距离减去牛i左边的线条,再减去(牛i右边的牛的数目*牛i的位置)就是右边的绝对值之和

如下图蓝色部分就是我们要减去的部分

有了图配合一下代码一下就能看出来了

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#define For(a,b) for(ll a=1;a<=b;a++)
#define mem(a,b) memset(a,b,sizeof(a))
#define _mem(a,b) memset(a,0,(b+1)<<2)
#define lowbit(a) ((a)&-(a))
using namespace std;
typedef long long ll;
const ll maxn =  1e5;
const ll INF = 0x3f3f3f3f;
ll c[2][maxn];
ll n;
struct edge{
    ll v,w;        
}e[maxn];
bool cmp(edge a,edge b){return a.v> n;
    For(i,n)
        cin >> e[i].v >> e[i].w;
    sort(e+1,e+1+n,cmp);
    ll ans = 0;
    ll cnl,cnr;
    ll bufn,bufw;
    ll all = 0;
    For(i,n){
        bufn = getsum(e[i].w,0);        //比牛i小的牛的个数
        bufw = getsum(e[i].w,1);        //比牛i小的牛的位置总和
        cnl = bufn*e[i].w-bufw;         //牛i左边
        cnr = all - bufw - (i-bufn-1)*e[i].w;//牛i右边
        ans += (cnl+cnr)*e[i].v;
        all += e[i].w;                  //总长
        update(e[i].w,0);
        update(e[i].w,1);
    }
    cout << ans << endl;

    return 0;
}