java数据结构总结——排序
(一)插入排序
时间复杂度:
最好情况:O(n)
最坏情况:O(n^2)
注:越有序越快
空间复杂度:O(1)
稳定性:稳定
public static void insertSort(int[] array) {
for (int i = 1; i < array.length; i++) {
int tmp = array[i];
int j = i-1;
for (; j >= 0 ; j--) {
if(array[j] > tmp) {
array[j+1] = array[j];
} else {
break;
}
}
array[j+1] = tmp;
}
}
(二)希尔排序
时间复杂度:O(n ^ 1.2 ) — O(n ^ 1.5)
注:越有序越快
空间复杂度:O(1)
稳定性:不稳定
public void shellSort(int[] array ,int gap) {
for (int i = gap; i < array.length ; i++) {
int tmp = array[i];
int j = i-gap;
for(;j >= 0;j-=gap) {
if(array[j] > tmp) {
array[j+gap] = array[j];
} else {
break;
}
}
array[j+gap] = tmp;
}
}


(三)选择排序
时间复杂度:O(n^2)
空间复杂度:O(1)
稳定性:不稳定
public void shellSort(int[] array ,int gap) {
for (int i = gap; i < array.length ; i++) {
int tmp = array[i];
int j = i-gap;
for(;j >= 0;j-=gap) {
if(array[j] > tmp) {
array[j+gap] = array[j];
} else {
break;
}
}
array[j+gap] = tmp;
}
}
(四)堆排序
时间复杂度:O(n*logn)
空间复杂度:O(1)
稳定性:不稳定
private void adjustDown(int[] array,int root,int len) {
int parent = root;
int child = 2*parent + 1;
while(child < len) {
if(child + 1 < len && array[child + 1] > array[child]) {
child++;
}
if(array[parent] > array[child]) {
int tmp = array[parent];
array[parent] = array[child];
array[child] = tmp;
parent = child;
child = 2*parent + 1;
} else {
break;
}
}
}
public void createHeap(int[] array) {
for (int i = (array.length-2)/2; i >= 0 ; i--) {
adjustDown(array,i,array.length);
}
}
public void heapSort(int[] array) {
int end = array.length-1;
while(end > 0) {
int tmp = array[0];
array[0] = array[end];
array[end] = tmp;
adjustDown(array,0,end);
end--;
}
}
(五)冒泡排序
时间复杂度:
最好情况:O(n)
最坏情况:O(n^2)
注:越有序越快
空间复杂度:O(1)
稳定性:稳定
public void bubbleSort(int[] array) {
for (int i = 0; i < array.length-1 ; i++) {
boolean flag = true;
for (int j = 0; j < array.length-1-i; j++) {
if(array[j] > array[j+1]) {
int tmp = array[j];
array[j] = array[j+1];
array[j+1] = tmp;
flag = false;
}
}
if(flag) {
break;
}
}
}
(六)快速排序
时间复杂度:
最好情况:O(n*logn)
最坏情况:O(n^2)
注:越有序越慢
空间复杂度:
最好情况:O(logn)
最坏情况:O(n)
稳定性:不稳定
1.递归法
private static void insert_Sort(int[] array,int start,int end) {
for (int i = start+1; i <= end ; i++) {
int tmp = array[i];
int j = i-1;
for (; j >= 0 ; j--) {
if(array[j] > tmp) {
array[j+1] = array[j];
} else {
break;
}
array[j+1] = tmp;
}
}
}
private static void swap(int[] array,int i,int j) {
int tmp = array[i];
array[i] = array[j];
array[j] = tmp;
}
private static void three_num(int[] array,int left,int right) {
int mid = (left+right)>>>1;
if(array[mid] > array[left]) {
swap(array,mid,left);
}
if(array[mid] > array[right]) {
swap(array,mid,right);
}
if(array[left] > array[right]) {
swap(array,left,right);
}
}
private static int partition(int[] array,int low,int high) {
int tmp = array[low];
while(low < high) {
while(low < high && array[high] >= tmp) {
high--;
}
array[low] = array[high];
while(low < high && array[low] <= tmp) {
low++;
}
array[high] = array[low];
}
array[low] = tmp;
return low;
}
public static void quick(int[] array,int left,int right) {
if(left >= right) {
return;
}
if(right-left+1 <= 100) {
insert_Sort(array,left,right);
return;
}
//使划分均匀
three_num(array,left,right);
int par = partition(array,left,right);
quick(array,left,par-1);
quick(array,par+1,right);
}
public static void quickSort(int[] array) {
quick(array,0,array.length-1);
}
2.非递归法
public static void quickSort1(int[] array) {
Stack<Integer> stack = new Stack<>();
int left = 0;
int right = array.length-1;
stack.push(left);
stack.push(right);
while (!stack.empty()) {
right = stack.pop();
left = stack.pop();
par = partition(array, left, right);
if (par > left + 1) {
stack.push(left);
stack.push(par - 1);
}
if (par < right - 1) {
stack.push(par + 1);
stack.push(right);
}
}
}
(七)归并排序
时间复杂度:O(n*logn)
空间复杂度:O(n)
稳定性:稳定
1.递归法:
public void merge(int[] array,int left,int mid,int right) {
int s1 = left;
int s2 = mid+1;
int[] ret = new int[right-left+1];
int i = 0;
while(s1 <= mid && s2 <= right) {
if(array[s1] <= array[s2]) {
ret[i++] = array[s1++];
} else {
ret[i++] = array[s2++];
}
}
while(s1 <= mid) {
ret[i++] = array[s1++];
}
while(s2 <= right) {
ret[i++] = array[s2++];
}
for (int j = 0; j < ret.length ; j++) {
array[j+left] = ret[j];
}
}
public void mergeSortInternal(int[] array,int left,int right) {
if(left >= right) {
return;
}
int mid = (left + right) /2;
mergeSortInternal(array,left,mid);
mergeSortInternal(array,mid+1,right);
merge(array,left,mid,right);
}
public void mergeSort(int[] array) {
mergeSortInternal(array,0,array.length-1);
}
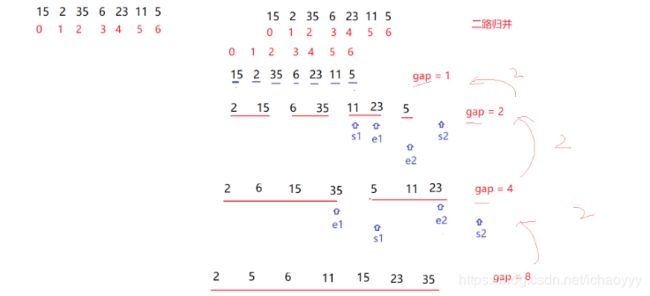
2.非递归法
public void mergeSort1(int[] array) {
for (int gap = 1; gap < array.length; gap*=2) {
mergeNor(array,gap);
}
}
public void mergeNor(int[] array,int gap) {
int s1 = 0;
int e1 = s1+gap-1;
int s2 = e1+1;
int e2 = s2+gap-1 < array.length ? s2+gap-1 : array.length-1;
int[] ret = new int[array.length];
int k = 0;
while(s2 < array.length) {
while(s1 <= e1 && s2 <= e2) {
if(array[s1] <= array[s2]) {
ret[k++] = array[s1++];
} else {
ret[k++] = array[s2++];
}
}
while(s1 <= e1) {
ret[k++] = array[s1++];
}
while(s2 <= e2) {
ret[k++] = array[s2++];
}
s1 = e2+1;
e1 = s1+gap-1;
s2 = e1 +1;
e2 = s2+gap-1 < array.length ? s2+gap-1 : array.length-1;
}
while(s1 < array.length) {
ret[k++] = array[s1++];
}
for (int i = 0; i < ret.length ; i++) {
array[i] = ret[i];
}
}