Torch实现ReQU，和梯度验证

重写函数

我们使用torch实现我们自己的ReQU模块。在实现一个新的layer之前，我们必须了解，我们并非重写forward和backward方法，而是重写里面调用的其他方法。
1）重新updataOutput方法，从而实现forward方法。
2）重写updataGradInput方法实现部分backward，计算loss函数相对于layer输入的导数，dloss/dx, 根据loss函数相对于layer输出的导数dloss：

3）重写accGradParameters方法实现backward其余部分，计算loss函数相对于权重的导数。

ReQU模块

Rectified Quadratic Unit（ReQU）与sigmoid和ReLU很相似，这个模块作用于每一个元素上：

用矩阵的方式来表达就是：

括号里如果是trues就返回1s，如果是falses就返回0s，中间的符号代表元素级别的乘积

重写updateOutput和updateGradInput模块

在重写模块之前，我们先推导公式，dloss/dx=dloss/dz.*dz/dx=dloss/dz.*2*(x>0).*x
我们首先重写updateOutput函数，这个函数主要计算输入为input时的输出：

function ReQU:updateOutput(input)
  self.output:resizeAs(input):copy(input)
  self.output:gt(input,0):cmul(input):cmul(input)
  return self.output
end

其中self.output:gt(input,0):cmul(input):cmul(input)这一步比较重要，self.output:gt(input,0)目的把input里面值与0比较，大于0设为1，否则设为0，然后通过两次cmul(input)，计算得到正确的输出。
我们然后重写updateGradInput函数，这个函数的目的是计算loss函数相对于输入的导数：

function ReQU:updateGradInput(input, gradOutput)
  self.gradInput:resizeAs(gradOutput):copy(gradOutput)
  self.gradInput:cmul(self.gradInput:gt(input,0):mul(2):cmul(input),gradOutput)
  return self.gradInput
end

输入是input和gradOutput，通过我们上面推到的公式，通过代码：
self.gradInput:cmul(self.gradInput:gt(input,0):mul(2):cmul(input),gradOutput)计算得到

构建一个简单神经网络

我们构建一个简单的神经网络，用来训练iris.data.csv里面的数据。我们定义一个function叫做create_model，创建model以及criterion。这个model包括：
Input——>linear——>non-linearity——>linear——>log softmax——>cross-entropy loss
Input一共有4个维度，non-linearity选择使用sigmoid或者ReQU。下面是model核心代码：

local model = nn.Sequential()
model:add(nn.Linear(n_inputs, embedding_dim))
if opt.nonlinearity_type == 'requ' then
  model:add(nn.ReQU())
elseif opt.nonlinearity_type == 'sigmoid' then
  model:add(nn.Sigmoid())
else
  error('undefined nonlinearity_type ' .. tostring(opt.nonlinearity_type))
end 
model:add(nn.Linear(embedding_dim, n_classes))
local criterion = nn.ClassNLLCriterion()

测试gradient

我们最后得到的cost function为E(w1,…,wn)，那么梯度就是分别针对wi求导数，公式如下：

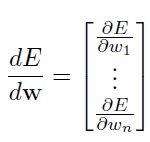
所以当计算梯度的时候，我们需要计算所有的偏导数。我们可以近似的计算偏导数如下：

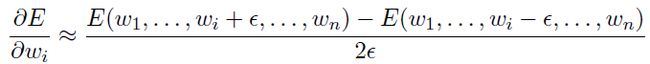
我们使用这个思想来测试我们的神经网络，我们把整个神经网络看成一个方程E(x;w)，然后随机生成x和w，然后利用上述公式估计梯度值，然后我们也使用公式求得认为正确的梯度值。如果这两个值相似，那么就可以判断我们写的“ReQU”是正确的，判断公式如下：

gi是使用两种方式求得的梯度，求得的值如果和ϵ的度相近，那么认为求得的梯度是正确的。
代码细节如下：
1） 求正确的梯度：

-- returns dloss(params)/dparams
local g = function(x)
  if x ~= parameters then
    parameters:copy(x)
  end
  gradParameters:zero()
  local outputs = model:forward(data.inputs)
  criterion:forward(outputs, data.targets)
  model:backward(data.inputs, criterion:backward(outputs, data.targets))
  return gradParameters
end

2） 求近似的梯度：

-- compute numeric approximations to gradient
local eps = eps or 1e-4
local grad_est = torch.DoubleTensor(grad:size())
for i = 1, grad:size(1) do
  x[i] = x[i] + eps
  local loss_a = f(x)
  x[i] = x[i] - 2*eps
  local loss_b = f(x)
  x[i] = x[i] + eps
  grad_est[i] = (loss_a-loss_b)/(2*eps)
end

3） 计算两个方法求得的梯度的差：

-- computes (symmetric) relative error of gradient
local diff = torch.norm(grad - grad_est) / torch.norm(grad + grad_est)

测试Jacobian

这里我们测试dz/dx计算的是否正确，我们计算Jacobian矩阵，我们如果有m个样本，每个样本为n维，那么这个Jacobian矩阵就是mxn的矩阵：

第i行是关于第i个样本input的梯度，其中fi表示输出output。我们如何获得Jacobian矩阵呢？这个矩阵是在backward的updateGradInput中隐性计算的：

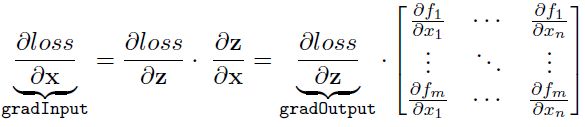
为了获得Jacobian矩阵，我们需要构造我们gradOutput vector，使其中一个为1，其余的全部为0，这样就能获得Jacobian一整行，torch代码如下：

local z = module:forward(x):clone()
local jac = torch.DoubleTensor(z:size(1), x:size(1))
-- get true Jacobian, ROW BY ROW
local one_hot = torch.zeros(z:size())
for i = 1, z:size(1) do
  one_hot[i] = 1
  jac[i]:copy(module:backward(x, one_hot))
  one_hot[i] = 0
end

我们使用与上一节类似的方法计算近似值：

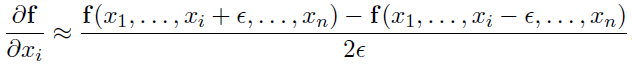
Torch代码如下：

-- compute finite-differences Jacobian, COLUMN BY COLUMN
local jac_est = torch.DoubleTensor(z:size(1), x:size(1))
for i = 1, x:size(1) do
  x[i] = x[i] + eps
  z_offset = module:forward(x):clone()
  x[i] = x[i] - 2*eps
  z_offset=z_offset-module:forward(x)
  x[i] = x[i] + eps
  jac_est[{{},i}]:copy(z_offset):div(2*eps)
end
-- computes (symmetric) relative error of gradient
local abs_diff = (jac - jac_est):abs()