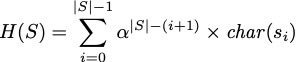Rabin-Karp算法：字符串匹配问题

为什么写这篇博客

其实有不少博客都有写Rabin-Karp算法，而且这个算法也非常简单易懂，但是很多人都说“该算法的理论复杂度是O(mn)，在实际生活中是O(m+n)”。

其实这个是不对的，在理论上，这个算法的复杂度也是O(m+n)。这篇文章就是想更深的一步讨论Rabin-Karp算法，解释为什么它的复杂度就应该是O(m+n)。

 

SubString Pattern Matching（字符串匹配/查重）

Rabin-Karp是用来解决字符串匹配（查重）的问题的。该问题的严谨定义如下：

Input：一段字符串t，和一个字符串p

Output：如果t中含有p，那么输出yes，如果没有，输出no

用大白话说，就是看p是不是t的子字符串，如果是的话，输出yes，如果不是的话，输出no

 

如何hashing字符串

比较笼统和宽泛的来说，哈希其实就是把一个定义域较宽的集合映射到一个值域较小的集合。一般来说，我们映射的结果是一个整数，也就是俗称的地址。比如说现在有一个数为x，我们希望进行哈希运算之后的H(x)是一个整数，然后我们把x放到哈希表中地址为H(x)的地方。

如果x是一个数字，这个理解起来比较直观，我们可以定义哈希函数为对这个数字的四则运算，得到一个新的数字，作为x的哈希值。

那么如果x是一个字符串S呢？如果通过一个哈希函数，把字符串S转换为一个整数呢？Hashing字符串一般用的是如下公式：

                                       

 

其中，代表的是S的定义域大小，比如说如果S全是英文字母，那么的值为26，因为英文字母就只有26个。然后这个函数是一个映射函数，映射S的定义域中的每一个字符到数字的函数。

根据上面的这个公式，就能把任意一个字符串S映射为一个整数。

 

Brute Force算法（暴力解法）

暴力破解Substring Pattern Matching的方法十分直观，过程如下：

假设字符串t的长度为n，字符串p的长度为m。

在字符串t上，放一个长度为m窗口window。

从头开始慢慢的滑动这个窗口window，每滑动一次，就把窗口里的内容和p对比一下。

如果一样，就返回yes。如果不一样，那么继续往右滑动一格窗口window。 

从上述算法可知，in worst case，一共会有(n-m+1)个窗口滑动。->这一步的复杂度是O(n)

然后每次窗口滑动，都涉及到两个长度为m的字符串的比较。->这一步的复杂度是O(m)

由于这两部是一个nested loop，所以最终的算法复杂度是O(m*n)。

 

Rabin-Karp算法

基本思想和暴力破解算法是一样的。也需要一个大小为m的窗口，但是不一样的是，不是直接比较两个长度为m的字符串，而是比较他们的哈希值。

同样的，现在我们做他们的复杂度分析，in worst case，一共会有(n-m+1)个窗口滑动。->这一步的复杂度是O(n)

这个是不变的，但是由于哈希值都是数字，所以两个数字的比较，只需要O(1)。

但是计算哈希值的时间呢？

在一开始的时候，我们需要计算p的哈希值，由于p的长度为m，所以计算p的哈希值的时间为O(m).

然后每一次移动窗口，都需要对窗口内的字符串计算哈希值，此时这个字符串的长度为m，所以计算它哈希值的时间也为O(m).如果照这样看，算法复杂度还是O(m*n)，和上面的暴力破解算法没有任何区别。

但是实际上，计算移动窗口内的哈希值并不需要O(m)，在已知前一个窗口的哈希值的情况下，计算当前窗口的哈希值，只需要O(1)的时间复杂度。

现在再来看上面提到的计算字符串哈希值的函数，假设现在窗口的起点在j这个位置，此时窗口内的字符串哈希值为：

                            

那么，当计算下一个窗口的哈希值时，也就是当窗口的起点为j+1时，哈希函数值可由如下方法计算：

                          

所以，这样看来，在计算出第一个窗口的函数值之后，后面的每一个窗口哈希值都可以根据上述公式计算，只需要做一次减法，一次乘法，一次加法。所以之后的每一次哈希值计算都是O(1)的复杂度。

那么重头来算一次复杂度：

一共有(n-m+1)个窗口，复杂度为O(n).

计算p的哈希值O(m)，计算第一个窗口的复杂度，O(m).

此后计算每一个窗口的复杂度O(1).

所以最终的复杂度是O(m+n)。