ICA（独立成分分析）方法及应用于视频分析心跳检测

本文整理自论文《Non-contact, automated cardiac pulse measurements using video imaging and blind source separation》及ICA相关资料。

独立成分分析（Independent Component Analysis，ICA），是一种数据驱动的信号分析方法，常用于盲源分离（Blind Source Separation，BSS）。

盲源分离是指在信号的理论模型和源信号无法精确获知的情况下，如何从混迭信号（观测信号）中分离出各源信号的过程。盲源分离和盲辨识是盲信号处理的两大类型。盲源分离的目的是求得源信号的最佳估计，盲辨识的目的是求得传输通道的混合矩阵。

最典型的盲源分离问题是鸡尾酒会问题（Cocktail Party Problem）：给定混合信号，分离出鸡尾酒会中同时说话的每个人的独立信号。

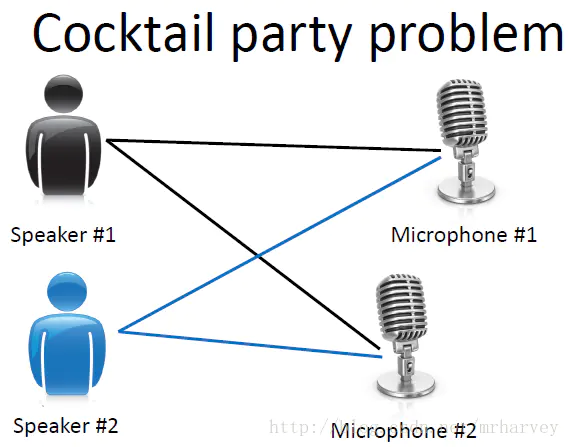
ICA原理

预处理
在进行ICA之前通常对数据进行去均值和白化，使用PCA处理，以保证混合矩阵为正交矩阵，且可将采集信号数目降到与源信号数目相等。

算法目标
源信号$s=[s_1,s_2,...,s_i{]}^T$经过线性组合得到采集信号$x=[x_1,x_2,...,x_i{]}^T$，其混合矩阵记为$W$，即$x=Ws$。假设$W$为满秩矩阵，则存在$W^{\prime }=W^{-1}$使$s=W^{\prime }x$，ICA的目标就是求出矩阵$W^{\prime }$，从而从$x$中还原出源信号$s$。

基本假设

1. 各源信号间独立
2. 至多有一个信号服从高斯分布，混合后信号不服从高斯分布
3. 变换为线性变换，且变换矩阵非时变

主要思路
ICA方法没有参照目标，需要自组织学习过程。其主要思路为：

1. 建立以$W$为变量的目标函数$L(W)$，当$L(W)$取到极值时的$W$即为所求结果。
2. 使用优化方法找到$L(W)$的极值，得到最终的$W$。

常使用的算法主要分为基于信息论方法和基于统计学方法。基于信息论方法主要有FastICA，Infomax，最大似然估计等方法，基于统计学方法主要有二阶累积量，四阶累积量等方法。下面简要介绍最大似然估计方法。

最大似然估计法
假设单个源信号$s_i$的概率密度为 $p(s_i)$，则全体源信号 $s$ 的联合分布为：
$$p(s)=\prod _{i=1}^{n}p(s_i)$$则经过$x=As=W^{-1}s$变换后$x$的概率分布为：
$$p(x)=\prod _{i=1}^{n}p(w_i^{T}x)\cdot |W|$$由基本假设得知不能选用高斯累积分布函数，令$p(x)$的累积分布函数为sigmoid函数$f(s)=\frac{1}{1+e^{-s}}$，则$p(x)=f^{\prime }(s)=f(s)(1-f(s))$。可得关于$W$的似然函数，式中m表示时间序列。
$$l(W)=\sum _{j=1}^m(\sum _{i=1}^n\log p(w_i^T{x}^j)+\log |W|)$$将$l(W)$关于W求导后可得到对于每一个x的梯度更新规则：
$$W:=W+\alpha \left(\left[\begin{array}{c}1-2f(w_1^{T}x)\\ 1-2f(w_2^{T}x)\\ ⋮\\ 1-2f(w_n^{T}x)\end{array}\right]x^T+(W^T{)}^{-1}\right)$$式中$\alpha$为学习率，当$W$收敛后可根据$s=Wx$由观测信号复原出源信号。

存在的问题

1. 分离结果幅度不确定
2. 分离信号排序不确定
3. 当观测信号数小于源信号数时无法分离

利用ICA方法进行视频分析心跳检测

基于ICA的方法，论文《Non-contact, automated cardiac pulse measurements using video imaging and blind source separation》提出了一种通过分析视频中人脸变化从而估计心跳频率的方法，该方法准确率较高，且对于一定程度的缓慢移动具有鲁棒性，并且可以同时检测多人，可以用于远程医疗等。
该方法基本原理为，人心跳时产生的血液输送会使面部大小发生轻微变化，从而对自然光照产生不同的反射结果，并且对于不同波长光的变化情况不同，因此在RGB三通道中表现出的变化情况也不相同。通过记录彩色视频RGB通道的不同变化情况，使用ICA方法进行分析，得到最接近真实心跳频率的信号源。
基本步骤

1. 使用opencv提供的人脸检测器对视频进行人脸区域检测并记录区域位置。
2. 将人脸区域图像分离为RGB三通道，分别计算区域内灰度均值。
3. 经过一段时间后可得到随时间变化的三个观测信号R,G,B。
4. 对R,G,B三个信号进行ICA分析，得到三个相互独立的源信号，进行傅里叶频谱分析，取其中最接近真实心跳频率范围的波峰作为测量结果。
   

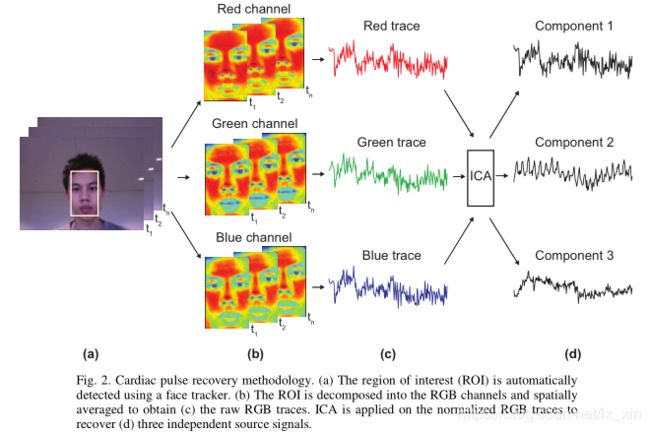
相关实验结果
静止检测结果：

缓慢运动检测结果：

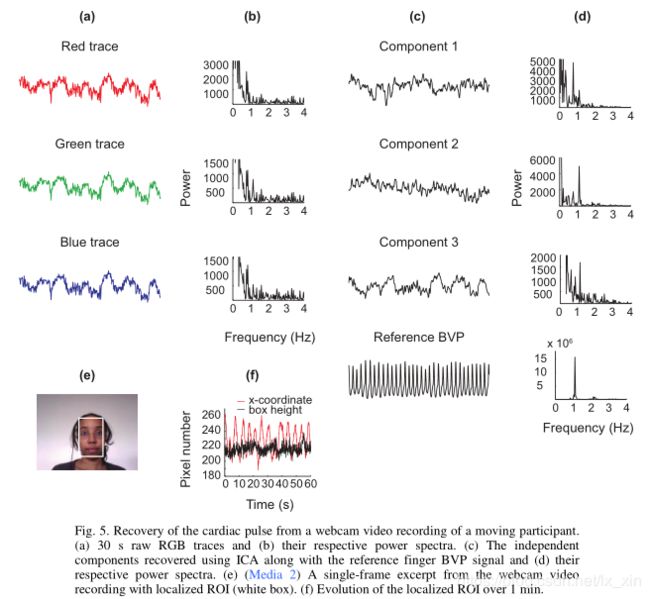
多人检测结果：

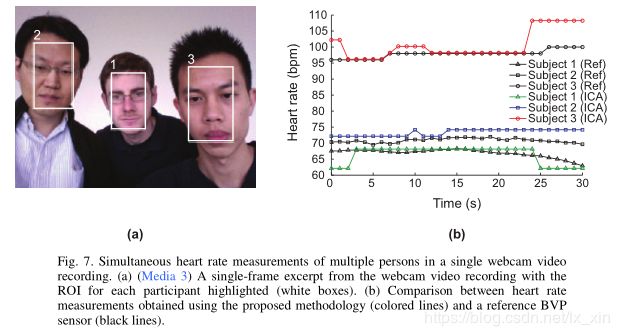
参考资料：

1. Ming-Zher Poh, Daniel J. McDuff,and Rosalind W. Picard .Non-contact, automated cardiac pulse measurements using video imaging and blind source separation[J].OPTICS EXPRESS，10 May 2010 ，Vol. 18, No. 10.
2. ICA及其在数字图像处理中的应用
3. 机器学习笔记—独立成分分析
4. 极大似然估计详解