L2和L1正则化防止过拟合-贝叶斯角度和约束优化角度的解释
文章目录
- L2正则化
- 约束优化角度
- 贝叶斯角度
- L1正则化
- 约束优化角度
- 贝叶斯角度
L1和L2正则化方法对于机器学习模型来说都具有防止模型过拟合的作用,通常我们需要理解他们是如何发挥作用的。L1、L2原理的解释可以从两个角度:
- 带约束条件的优化求解(拉格朗日乘子法)
- 贝叶斯学派:最大后验概率
- L1正则化相当于为参数w加入了拉普拉斯分布的先验。
- L2正则化相当于为参数w加入了高斯分布的先验。
L2正则化
约束优化角度
正则化是一种回归的形式,它将系数估计朝零的方向进行约束、调整或缩小。也就是说,正则化可以在学习过程中降低模型复杂度和不稳定程度,从而避免过拟合的危险。在机器学习任务中,对于一个参数模型,优化参数时一定伴随着损失函数的建立与优化。
我们首先来看下不加入L2正则化的模型损失函数:
J L 2 ( w ) = L ( w ) J_{L2}(w) = L(w) JL2(w)=L(w)
加入L2正则化后的模型损失函数为:
J L 2 ( w ) = L ( w ) + λ 2 n w 2 J_{L2}(w) = L(w) + \frac{\lambda}{2n}w^2 JL2(w)=L(w)+2nλw2
所以L2正则化的方式就是在原来损失函数的基础上,再加上模型参数的值的平方即可。其中等号右边的前半部分称为经验风险,后半部分称为结构风险。
对于原始损失函数求一阶导为:
δ L ( w ) δ w = d 0 \frac{\delta L(w)}{\delta w} = d_0 δwδL(w)=d0
对于加入L2正则的损失函数求一阶导为:
δ J L 2 ( w ) δ w = d 0 + λ n w \frac{\delta J_{L2}(w)}{\delta w} = d_0 + \frac{\lambda}{n}w δwδJL2(w)=d0+nλw
好,到这里我们知道加入L2正则化的损失函数求导后多个一个关于w的项。
在优化模型过程中,一般会选择相应的优化算法,例如选择SGD优化算法时,参数w更新公式为:
其中,
lr表示学习率 learning rate.
w = w − l r ∗ δ L ( w ) δ w w = w - lr*\frac{\delta L(w)}{\delta w} w=w−lr∗δwδL(w)
如果使用L2正则后的模型更新参数w公式为:
w = w − l r ∗ δ L ( w ) δ w − l r ∗ λ n w w = w - lr*\frac{\delta L(w)}{\delta w} - \frac{lr*\lambda}{n}w w=w−lr∗δwδL(w)−nlr∗λw
= ( 1 − l r ∗ λ n ) ∗ w − l r ∗ δ L ( w ) δ w = (1 - \frac{lr*\lambda}{n})*w - lr*\frac{\delta L(w)}{\delta w} =(1−nlr∗λ)∗w−lr∗δwδL(w)
可以看出来使用原始损失函数的一阶导数时,w的权重是1,加入L2正则后,w的权重一定小于1,也就是对模型进行了衰减。
L2的权值更新公式为
wi = wi – η * wi,虽然权值不断减小,但每次减小的幅度不断降低,所以很快会收敛到较小的值但不为0。
在过拟合问题中,模型的参数越大,模型过拟合的风险越大,而模型参数越小,模型越不容易过拟合。因此通过加入L2正则化,对模型参数进行衰减,从而减小了过拟合的风险。
贝叶斯角度
上面是从优化函数角度解释L2正则化方式防止过拟合的原因,那么如果从贝叶斯角度如何理解呢?
为L(w)加入正则项,相当于为模型的参数 w 加入先验,那要求w满足某一分布。
下面先介绍下高斯分布。高斯分布又称正态分布,是常见的连续概率分布。高斯分布的概率密度函数为:
f ( x ) = 1 σ 2 π e − ( x − μ ) 2 2 σ 2 f(x) = \frac{1}{\sigma \sqrt{2 \pi}} e^{-\frac{(x-\mu)^2}{2\sigma^2}} f(x)=σ2π1e−2σ2(x−μ)2
其曲线图如下所示:
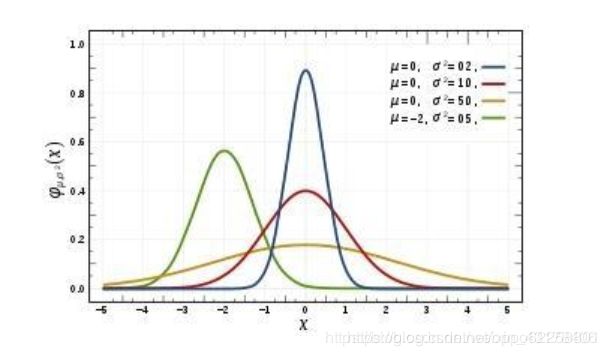
那么高斯分布和L2正则化是怎联系上的呢?
我们知道在最大似然估计中,是假设权重w是未知的参数,从而求得对数似然函数(取了log):
l ( w ) = l o g [ P ( y ∣ X ; w ) ] = l o g [ ∏ ϵ P ( y i ∣ x i ; w ) ] ( ∗ ) l(w) = log[P(y|X;w)] = log[\prod_\epsilon P(y^i|x^i;w)] \qquad (*) l(w)=log[P(y∣X;w)]=log[ϵ∏P(yi∣xi;w)](∗)
从上面可以看出,对于y^i不同的概率分布,就可以得到不同的模型。
若我们假设满足
y i ∽ N ( w T x i , σ 2 ) y^i \backsim N(w^T x^i, \sigma^2) yi∽N(wTxi,σ2)
的高斯分布,我们则可以在公式(*)中带入高斯分布的概率密度函数:
l ( w ) = l o g [ ∏ i 1 2 π σ e − ( y i − w T x i ) 2 2 σ 2 ] l(w) = log[\prod_i \frac{1}{\sqrt{2\pi} \sigma}e^{-\frac{(y^i - w^T x^i)^2}{2\sigma^2}}] l(w)=log[i∏2πσ1e−2σ2(yi−wTxi)2]
= − 1 2 σ 2 ∑ i ( y i − w T x i ) 2 + C \qquad\qquad = -\frac{1}{2\sigma^2}\sum_i (y^i - w^T x^i)^2 + C =−2σ21i∑(yi−wTxi)2+C
上面的C为常数项。常数项和系数不影响我们求解max(l(w))的解,所我们可以令
J ( w ; X , y ) = − l ( w ) J(w;X, y) = -l(w) J(w;X,y)=−l(w)
这样其实是得到了Linear Regression的代价函数。
而在最大化后验概率估计中,我们将权重w看作随机变量,也具有某种分布,从而有:
P ( w ∣ X , y ) = P ( w , X , y ) P ( X , y ) = P ( X , y ∣ w ) P ( w ) P ( X , y ) ∝ P ( y ∣ X , w ) P ( w ) P(w|X, y) = \frac{P(w, X, y)}{P(X, y)} = \frac{P(X, y|w)P(w)}{P(X, y)}\propto P(y|X, w)P(w) P(w∣X,y)=P(X,y)P(w,X,y)=P(X,y)P(X,y∣w)P(w)∝P(y∣X,w)P(w)
取对数后得到:
M A P = l o g P ( y ∣ X , w ) P ( w ) = l o g P ( y ∣ X , w ) + l o g P ( w ) MAP = log P(y|X, w)P(w) = log P(y|X, w) + log P(w) MAP=logP(y∣X,w)P(w)=logP(y∣X,w)+logP(w)
可见,后验概率函数是在似然函数基础上再加上logP(w),P(w)的意义是对权重系数w的概率分布的先验假设,在收集到训练样本{X, y}之后,则可根据{X, y}的后验概率对w进行修正,从而对w做出更好的估计。
若假设w的先验分布为0均值的高斯分布,即:
w j ∽ N ( 0 , σ 2 ) w_j \backsim N(0, \sigma^2) wj∽N(0,σ2)
则有:
l o g ( P ( w ) ) = l o g ∏ j P ( w j ) = l o g ∏ j [ 1 2 π σ e − w j 2 2 σ 2 ] log(P(w)) = log\prod_j P(w_j)= log\prod_j[\frac{1}{\sqrt{2\pi} \sigma}e^{-\frac{w_j^2}{2\sigma^2}}] log(P(w))=logj∏P(wj)=logj∏[2πσ1e−2σ2wj2]
= − 1 2 σ 2 ∑ w j 2 + C \qquad = -\frac{1}{2\sigma^2} \sum w_j^2 + C =−2σ21∑wj2+C
可以看到,在高斯分布下,logP(w)的效果等价于在损失函数中增加L2正则化。
所以,L2正则化可通过假设权重w的先验分布为高斯分布,由最大后验概率估计导出。
L1正则化
约束优化角度
L1正则化具有防止模型过拟合的能力,但是相比于L2正则化,两者防止过拟合的方式不太一样。
不加入L1正则化的损失函数为
J L 1 ( w ) = L ( w ) J_{L1}(w) = L(w) JL1(w)=L(w)
加入L1正则化的损失函数为
J L 1 ( w ) = L ( w ) + λ ∣ w ∣ J_{L1}(w) = L(w) + \lambda|w| JL1(w)=L(w)+λ∣w∣
为什么新的损失函数可以防止模型的过拟合呢?
我们经常在一些文章或者博客中看到L1防止过拟合的方式是因为L1正则化有特征选择的作用,容易产生稀疏解,即可以使得重要特征的参数不为0,而使得一些不重要特征的参数变为0将其抛弃掉。
那么究竟为什么L1具有特征选择的作用,是如何将不重要特征的参数学习的结果为0的呢?
我们在优化更新参数w的时候,一般需要对损失函数求解一阶导数,对原始损失函数求解在w=0处的一阶导数为:
δ L δ w = d 0 \frac{\delta L}{\delta w} = d_{0} δwδL=d0
则引入L1正则项后,求解w=0的一阶导数为:
δ J L 1 ( w ) δ w ∣ w = 0 − = d 0 − λ \frac{\delta J_{L1}(w)}{\delta w} |_{w=0^-}= d_{0} - \lambda δwδJL1(w)∣w=0−=d0−λ
δ J L 1 ( w ) δ w ∣ w = 0 + = d 0 + λ \frac{\delta J_{L1}(w)}{\delta w} |_{w=0^+}= d_{0} + \lambda δwδJL1(w)∣w=0+=d0+λ
可见引入L1正则后,在0处的导数有一个突变,从d0−λ变到d0+λ。
若d0−λ和d0+λ异号,则在0处会是一个极小值点,因此,参数优化时很有可能优化到该极小值点上,即w=0处,当有多个参数时也是类似的情况,因此用L1正则化容易产生稀疏解。
其实L1正则化的权值更新公式为
wi = wi – η * 1, 权值每次更新都固定减少一个特定的值η,那么经过若干次迭代之后,权值就有可能减少到0。
上面我们知道L1正则化可以通过让模型学习更多稀疏解,而使得更多的参数变为0,当一个模型中有很多0值参数时,其模型复杂度会变得更小,从而给予模型防止过拟合的能力。
贝叶斯角度
先来介绍下拉普拉斯分布:
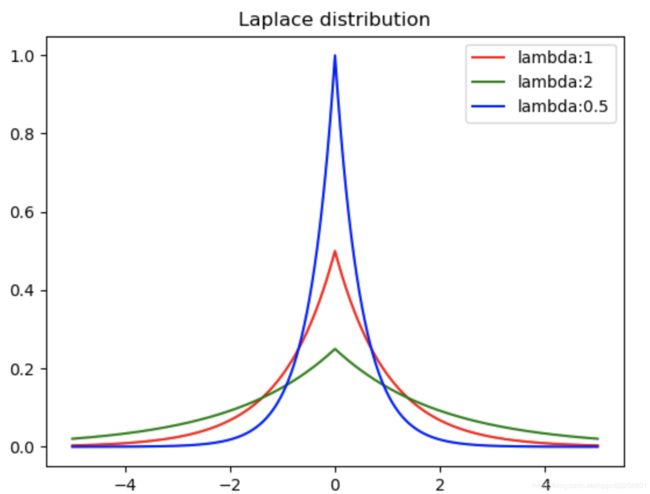
上面是拉普拉斯分布曲线,其对应公式为:
p ( x ) = 1 2 λ e − ∣ x − μ ∣ λ p(x) = \frac{1}{2\lambda} e^{-\frac{|x-\mu|}{\lambda}} p(x)=2λ1e−λ∣x−μ∣
一般的取值为0,所以形式如下:
p ( x ) = 1 2 λ e − ∣ x ∣ λ p(x) = \frac{1}{2\lambda} e^{-\frac{|x|}{\lambda}} p(x)=2λ1e−λ∣x∣
由于其是由两个指数函数组成,因此又叫双指数函数分布。
若假设w_j服从均值为0、参数为a的拉普拉斯分布,即:
P ( w j ) = 1 2 a e − ∣ w j ∣ a P(w_j) = \frac{1}{\sqrt{2a}} e^{\frac{-|w_j|}{a}} P(wj)=2a1ea−∣wj∣
则有:
l o g ( P ( w ) ) = l o g ∏ j 1 2 a e − ∣ w j ∣ a log(P(w)) = log \prod_j \frac{1}{\sqrt{2a}}e^{\frac{-|w_j|}{a}} log(P(w))=logj∏2a1ea−∣wj∣
= − 1 a ∑ j ∣ w j ∣ + C \qquad\qquad = -\frac{1}{a} \sum_j |w_j| + C =−a1j∑∣wj∣+C
上面的C为常数项。可以看到,在拉普拉斯分布下logP(w)的效果等价在代价函数中增加L1项。
所以,L1正则化可通过假设权重w的先验分布为拉普拉斯分布,由最大后验概率估计导出。