拉格朗日乘子法、对偶、KTT
拉格朗日乘子法、对偶、KTT
一般情况下,最优化问题分为三类
一、 无约束条件下的最优化问题
这种最优化问题比较简单,直接求导为0就可以得到。
二、 等式约束下的最优化问题
即除了目标函数之外,还有一些约束条件。假设目标函数为 f ( x ) f(x) f(x),约束条件为 h k ( x ) h_k(x) hk(x),这里的 k k k用来表示有 k k k个约束条件。
m i n f ( x ) minf(x) minf(x)
s . t . h k ( x ) = 0 k = 1 , 2 , 3.. s.t. h_k(x) = 0 \quad k = 1,2,3.. s.t.hk(x)=0k=1,2,3..
求这样的最优化问题有两种方法:
一种是使用消元法来解,但是这种方法有的时候很难求解,甚至无解。
另一种方法便是使用拉格朗日乘子法,其求解步骤分为三步:
- 构造拉格朗日函数
- 求解变量的偏导方程
- 代入目标函数
具体步骤如下:
- 首先构造一个拉格朗日函数,我们令
F ( x , λ , l ) = f ( x ) + ∑ k = 1 l λ k h k ( x ) F(x,λ,l) = f(x) + \sum_{k=1}^lλ_kh_k(x) F(x,λ,l)=f(x)+k=1∑lλkhk(x)
其中 λ k \lambda_k λk是第k个约束条件系数,又叫拉格朗日乘子。注意这里的 F ( x , λ , l ) F(x,\lambda,l) F(x,λ,l)是对 x , λ , l x,\lambda,l x,λ,l三个变量的函数。
- 于是我们分别对 x , λ , l x,\lambda,l x,λ,l变量求偏导数为0的解,得出来的解代入目标函数便是函数在等式约束条件。
为什么这样求解得到的便是我们想要得到的约束极值呢?我们可以用图来直观的解释一下:
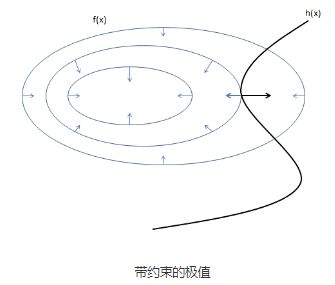
图中的圆圈表示目标函数与 , f ( x , y ) ,f(x,y) ,f(x,y)投影在平面上的等值线,每个全圆圈上的值相等,黑丝的曲线表示约束条件 h ( x ) = 0 h(x)=0 h(x)=0的函数图像。等值线与曲线相交的点,便是满足约束的点,于是我们所需要的极值点只有等值线与黑线相切的地方取到。
为什么只有相切的地方才可能是极值点,而相交的地方不是呢?假设相交的点是极值点的话,那么沿着 f ( x ) f(x) f(x)的曲线向两边走,一定还有其他的点和他相交,这就意味着 f ( x , y ) f(x,y) f(x,y)的值还能变大和变小(极值点的两侧是同时变大或者同时变小的),明显与我们的假设相悖,所以交点不是极值点。
而对于切点来说,沿着 h ( x ) h(x) h(x)曲线两边走, f ( x , y ) f(x,y) f(x,y)的值只能同时变大或者同时变小,这就符合了极值点的定义。
既然极值点在切点上,那么这两个函数在这一点的梯度应该在同一条直线上,方向可以相同或者相反(梯度的方向与等高线的切线是垂直,这个定理的相关推导可以自行百度)。
所以,满足条件的极值点一定满足: ∇ f ( x , y ) = λ ∇ h ( x , y ) ∇f(x,y)=λ∇h(x,y) ∇f(x,y)=λ∇h(x,y)(其中λ可以取0,取0表示目标函数的极值点刚好也在这一点),于是我们只用和原方程 h ( x , y ) = 0 h(x,y)=0 h(x,y)=0联立,然后只要解出这个方程组,就可以得到最优解,当然,这个方程可能存在解不出来的情况.
于是我们就可以把原来的优化问题写成 f ( x , y ) + λ h ( x , y ) f(x,y)+λh(x,y) f(x,y)+λh(x,y) 的形式,然后分别的对 x , y , λ x,y,λ x,y,λ求导,然后令偏导数为0就可以得到上面推来的式子了。这种方法就是拉格朗日乘子法。即:
∇ f ( x , y ) = ( ∂ f ∂ y , ∂ f ∂ x ) ∇f(x,y)=(\frac{\partial{f}}{\partial{y}},\frac{\partial{f}}{\partial{x}}) ∇f(x,y)=(∂y∂f,∂x∂f)
λ ∇ h ( x , y ) = ( λ ∂ h ∂ y , λ ∂ h ∂ x ) λ∇h(x,y)=(λ\frac{\partial{h}}{\partial{y}},λ\frac{\partial{h}}{\partial{x}}) λ∇h(x,y)=(λ∂y∂h,λ∂x∂h)
由于 ∇ f ( x , y ) = λ ∇ h ( x , y ) ∇f(x,y)=λ∇h(x,y) ∇f(x,y)=λ∇h(x,y),则
∂ f ∂ y = λ ∂ h ∂ y \frac{\partial{f}}{\partial{y}}=λ\frac{\partial{h}}{\partial{y}} ∂y∂f=λ∂y∂h
∂ f ∂ x = λ ∂ h ∂ x \frac{\partial{f}}{\partial{x}}=λ\frac{\partial{h}}{\partial{x}} ∂x∂f=λ∂x∂h
对 f ( x , y ) + λ h ( x , y ) f(x,y)+λh(x,y) f(x,y)+λh(x,y),分别对 x , y , λ x,y,λ x,y,λ求偏导:
对x求偏导:
∂ f ∂ x + λ ∂ h ∂ x + h ( x , y ) = 0 \frac{\partial{f}}{\partial{x}} + λ\frac{\partial{h}}{\partial{x}} + h(x,y)=0 ∂x∂f+λ∂x∂h+h(x,y)=0
对y求偏导:
∂ f ∂ y + λ ∂ h ∂ y + h ( x , y ) = 0 \frac{\partial{f}}{\partial{y}} + λ\frac{\partial{h}}{\partial{y}} + h(x,y)=0 ∂y∂f+λ∂y∂h+h(x,y)=0
对λ求偏导:
h ( x , y ) = 0 h(x,y)=0 h(x,y)=0
根据这三个式子化简后,可以看到公式 f ( x , y ) + λ h ( x , y ) f(x,y)+λh(x,y) f(x,y)+λh(x,y),分别对 x , y , λ x,y,λ x,y,λ求偏导和 ∇ f ( x , y ) = λ ∇ h ( x , y ) ∇f(x,y)=λ∇h(x,y) ∇f(x,y)=λ∇h(x,y)等价。
这里的红色的平面和蓝色的球面分别代表了两个约束 h 1 ( x ) h1(x) h1(x)和 h 2 ( x ) h2(x) h2(x),那么这个问题的可行域就是它们相交的那个圆。这里蓝色箭头表示平面的梯度,黑色箭头表示球面的梯度,那么相交的圆的梯度就是它们的线性组合(只是直观上的,类似向量的加法),所以在极值点的地方目标函数的梯度和约束的梯度的线性组合在一条直线上。所以就满足:
∇ f ( x ) = λ ∑ i = 1 2 u i ∇ h i ( x ) = ∑ i = 1 2 λ 2 ∇ h i ( x ) ∇f(x)=λ\sum_{i=1}^2u_i∇h_i(x)=\sum_{i=1}^2λ_2∇h_i(x) ∇f(x)=λi=1∑2ui∇hi(x)=i=1∑2λ2∇hi(x)
h 1 ( x ) = 0 h_1(x)=0 h1(x)=0
h 2 ( x ) = 0 h_2(x)=0 h2(x)=0
大于2个约束的情况也一样。为了好记,将原来的约束的问题写成:
(1) L ( x , λ ) = f ( x ) + ∑ i = 1 n λ i ∇ h i ( x ) L(x,λ)=f(x)+\sum_{i=1}^nλ_i∇h_i(x)\tag{1} L(x,λ)=f(x)+i=1∑nλi∇hi(x)(1)
然后对 x、λ 求偏导,然后让它们为0,得到的就是上式。
三、 既有等式约束,又有不等式约束的情况
m i n f ( x ) minf(x) minf(x)
s . t . h i ( x ) = 0 , i = 1 , 2 , . . . k s.t. h_i(x)=0, i=1,2,...k s.t.hi(x)=0,i=1,2,...k
c j ( x ) ≤ 0 , j = 1 , 2 , . . . l c_j(x)≤0, j=1,2,...l cj(x)≤0,j=1,2,...l
f ( x ) , h i ( x ) , c i ( x ) f(x),h_i(x),c_i(x) f(x),hi(x),ci(x)要求在定义域上是连续可微函数
注: 这里的等式和不等式约束公式只是一种表述的方式,现实中遇的可能与其略有不同,但是稍加转换便可以转换成上述的形式。
引入广义拉格朗日(generalized Lagrange function):
(2) L ( x , α , β ) = f ( x ) + ∑ j = 1 l β j h j ( x ) + ∑ i = 1 k α i c i ( x ) L(x,α,β) = f(x) +\sum_{j=1}^lβ_jh_j(x)+ \sum_{i=1}^kα_ic_i(x)\tag{2} L(x,α,β)=f(x)+j=1∑lβjhj(x)+i=1∑kαici(x)(2)
这个式子和上面的公式一不同的是,这里特别要求 α i > 0 α_i>0 αi>0,为什么这么要求我们后面再讲,先解释一下这个式子。这里 , α , β ,α,β ,α,β是拉格朗日乘子(其实就是函数的系数), x = ( x ( 1 ) , x = ( x ( 2 ) , . . . , x = ( x ( 3 ) ) ∈ R n x=(x^{(1)},x=(x^{(2)},...,x=(x^{(3)})\in R^n x=(x(1),x=(x(2),...,x=(x(3))∈Rn。
现在把 L ( x , α , β ) L(x,\alpha,\beta) L(x,α,β)看做关于 α i , β j \alpha_i,\beta_j αi,βj的函数,现在求其最大值,即求:
max α , β : α i ≥ 0 L ( x , α , β ) \max_{\alpha,\beta:\alpha_i\geq0}L(x,\alpha,\beta) α,β:αi≥0maxL(x,α,β)
这里 L ( x , α , β ) L(x,\alpha,\beta) L(x,α,β)是 α i , β j \alpha_i,\beta_j αi,βj的函数,目标就是确定 α i , β j \alpha_i,\beta_j αi,βj的值,使得 L ( x , α , β ) L(x,\alpha,\beta) L(x,α,β)能取到最大值,确定了 α i , β j \alpha_i,\beta_j αi,βj的值之后,上式就是一个之和 x x x有关的函数(多元函数求极值,对每个参数的偏导都为0的道理),定义这个函数为:
θ p ( x ) = max α , β , α i ≥ 0 L ( x , α , β ) θ_p(x) = \max_{α,β,α_i\ge0}{L(x,α,β)} θp(x)=α,β,αi≥0maxL(x,α,β)
其 中 L ( x , α , β ) = f ( x ) + ∑ j = 1 l β j h j ( x ) + ∑ i = 1 k α i c i ( x ) 其中L(x,α,β) = f(x) +\sum_{j=1}^lβ_jh_j(x)+ \sum_{i=1}^kα_ic_i(x) 其中L(x,α,β)=f(x)+j=1∑lβjhj(x)+i=1∑kαici(x)
下面我们讨论一下 x x x取值和 θ p ( x ) θ_p(x) θp(x)之间的关系.
当某个 x x x不满足 h i ( x ) , c i ( x ) h_i(x),c_i(x) hi(x),ci(x)的约束 ,即 h i ( x ) ≠ 0 h_i(x)\neq0 hi(x)̸=0或者 c i ( x ) > 0 c_i(x)>0 ci(x)>0时, max α , β , α i ≥ 0 L ( x , α , β ) = + ∞ \max_{α,β,α_i\ge0}{L(x,α,β)} = +\infty maxα,β,αi≥0L(x,α,β)=+∞.
原因:首先这里的 α i , β j \alpha_i,\beta_j αi,βj是我们刚才在求解函数最大值时已经确定的,若 h i ( x ) ≠ 0 h_i(x)\neq0 hi(x)̸=0,考虑下求偏导的情况,我们求出来的 β i \beta_i βi很容易可以取值使得原函数取到正无穷(既然求能使函数取最大值的 β i \beta_i βi,如果可以,肯定取可以使其函数能得最大值得 β \beta β),同理,.当 c i ( x ) > 0 c_i(x)>0 ci(x)>0时, a i {a_i} ai可以取 + ∞ {+\infty} +∞,使得 L ( x , α , β ) = + ∞ {L(x,\alpha,\beta)}=+\infty L(x,α,β)=+∞,于是,我们可以证明,当某个 x x x不满足 h i ( x ) , c i ( x ) h_i(x),c_i(x) hi(x),ci(x)的约束 ,即 h i ( x ) ≠ 0 h_i(x)\neq0 hi(x)̸=0或者 c i ( x ) > 0 c_i(x)>0 ci(x)>0时, max α , β , α i ≥ 0 L ( x , α , β ) = + ∞ \max_{α,β,α_i\ge0}{L(x,α,β)} = +\infty maxα,β,αi≥0L(x,α,β)=+∞.
当 x x x满足约束时,显然 L ( x , α , β ) = f ( x ) L(x,\alpha,\beta) = f(x) L(x,α,β)=f(x).
综上我们可得:
θ p ( x ) = max α , β , α i ≥ 0 L ( x , α , β ) = { + ∞ , 其他 f ( x ) , 如果x满足约束 θ_p(x) = \max_{α,β,α_i\ge0}{L(x,α,β)}= \begin{cases} +\infty, & \text{其他} \\ f(x), & \text{如果{x}满足约束} \end{cases} θp(x)=α,β,αi≥0maxL(x,α,β)={+∞,f(x),其他如果x满足约束
在满足约束的条件下,我们求 θ p ( x ) \theta_p(x) θp(x)的最小值,即:
min x θ p ( x ) = min x f ( x ) = min x max x , α , β L ( x , α , β ) \min_x\theta_p(x) = \min_xf(x) = \min_x\max_{x,α,β}L(x,α,β) xminθp(x)=xminf(x)=xminx,α,βmaxL(x,α,β)
而在不满足约束的情况下 θ p ( x ) = + ∞ {θ_p(x)} = +\infty θp(x)=+∞,显然不可能是最小值,于是,我们的目标,求解约束条件下 m i n f ( x ) minf(x) minf(x)最优解的问题就可以转化成求解 min x max x , α , β L ( x , α , β ) \min_x\max_{x,α,β}L(x,α,β) minxmaxx,α,βL(x,α,β)的无约束问题(这个式子被称为广义拉格朗日函数的极小极大问题),这样,就成功的把约束条件给去掉了.使用 p p p来表示原始问题,于是原始问题的最优解 p ∗ p^* p∗就可以表示如下:
p ∗ = min x θ p ( x ) p^*=\min_xθ_p(x) p∗=xminθp(x)
对偶问题
定义一个关于 α , β α,β α,β的函数:
θ D ( α , β ) = min x L ( x , α , β ) θ_D(α,β) = \min_xL(x,α,β) θD(α,β)=xminL(x,α,β)
考虑极大化 θ D ( α , β ) θ_D(α,β) θD(α,β),即:
max α , β : α ≥ 0 θ D ( α , β ) = max α , β : α ≥ 0 min x L ( x , α , β ) \max_{α,β:α\geq0}θ_D(α,β) = \max_{α,β:α\geq0}\min_xL(x,α,β) α,β:α≥0maxθD(α,β)=α,β:α≥0maxxminL(x,α,β)
这个式子被称为广义拉格朗日函数的极大极小问题,也被称为原始问题的对偶问题.对偶问题的最优值用 d ∗ d^* d∗表示:
d ∗ = max α , β : α ≥ 0 θ D ( α , β ) d^*=\max_{α,β:α\geq0}θ_D(α,β) d∗=α,β:α≥0maxθD(α,β)
对比原始问题,对偶问题是先求关于函数关于 x x x的最小化问题,之后再求函数关于 α , β α,β α,β最大化问题.而原始问题恰恰相反,是求函数关于 α , β α,β α,β的最大化问题,之后再求关于 x x x的最小化问题.总是是求函数关于α,β最大化和关于 x x x的最小化的问题,只是求解的顺序有所不同.
那么对偶问题和原始问题有什么关系呢?
定理1:若对偶问题和原始问题都有最优值,则:
d ∗ = max α , β : α ≥ 0 min x L ( x , α , β ) ≤ min x max x , α , β L ( x , α , β ) = p ∗ d^*=\max_{α,β:α\geq0}\min_xL(x,α,β)\leq\min_x\max_{x,α,β}L(x,α,β)=p^* d∗=α,β:α≥0maxxminL(x,α,β)≤xminx,α,βmaxL(x,α,β)=p∗
即:对偶问题的最优值不大于原始问题的最优值(弱对偶(weak duality)).
证明:
θ D ( α , β ) = min x L ( x , α , β ) ≤ max x , α , β L ( x , α , β ) ≤ θ p ( x ) ∗ θ_D(α,β) = \min_xL(x,α,β)\leq\max_{x,α,β}L(x,α,β)\leqθ_p(x)* θD(α,β)=xminL(x,α,β)≤x,α,βmaxL(x,α,β)≤θp(x)∗
即:
θ D ( α , β ) ≤ θ p ( x ) \theta_D(α,β) \leq\theta_p(x) θD(α,β)≤θp(x)
因为对偶问题和原始问题都有最优值,所以:
max x , α , β θ D ( α , β ) ≤ min x θ p ( x ) \max_{x,α,β}θ_D(α,β)\leq\min_{x}θ_p(x) x,α,βmaxθD(α,β)≤xminθp(x)
所以:
d ∗ = max α , β : α ≥ 0 min x L ( x , α , β ) ≤ min x max x , α , β L ( x , α , β ) = p ∗ d^*=\max_{α,β:α\geq0}\min_xL(x,α,β)\leq\min_x\max_{x,α,β}L(x,α,β)=p^* d∗=α,β:α≥0maxxminL(x,α,β)≤xminx,α,βmaxL(x,α,β)=p∗
原问题得证.
这些有什么用呢?
推论1: 如果 x ∗ , α ∗ , β ∗ x^*,α^*,β^* x∗,α∗,β∗分别是原始问题和对偶问题的可行解,并且 p ∗ = d ∗ p^*=d^* p∗=d∗(即原始问题和对偶问题在可行解 x ∗ , α ∗ , β ∗ x^*,α^*,β^* x∗,α∗,β∗上的取的最优值相同,这被称为强对偶(strong duality)),则 x ∗ , α ∗ , β ∗ x^*,α^*,β^* x∗,α∗,β∗分别是原始问题和对偶的最优解.
于是,当原始问题不好求解而对偶问题相对好求解的时候,这时我们就可以用求解对偶问题替代求解原始问题.并且更重要的是,对偶问题是一个凸优化问题,他的极值是唯一的(因为 d ∗ < p ∗ d^*<p^* d∗<p∗).这样无论一个问题是不是凸优化的问题,我们都能将其转化成凸优化的问题
新的问题又来了,什么情况下才能使得 p ∗ = d ∗ p^*=d^* p∗=d∗呢?这就是KTT条件.
定理2: 假设函数*f(x)*和 c i ( x ) c_i(x) ci(x)都是凸函数, h j ( x ) h_j(x) hj(x)是仿射函数(由一阶多项式构成的函数),并且不等式约束 c i ( x ) c_i(x) ci(x)是严格可行的,即存在 x x x,对所有的 i i i,都使得 c i ( x ) < 0 c_i(x)<0 ci(x)<0(注意这里是严格要求小于0,而不是小于等于0),则存在 x ∗ , α ∗ , β ∗ x^*,α^*,β^* x∗,α∗,β∗使得 x ∗ x^* x∗是原始问题的解, α ∗ , β ∗ α^*,β^* α∗,β∗是对偶问题的解,并且
p ∗ = d ∗ = L ( x ∗ , α ∗ , β ∗ ) p^*=d^*=L(x^*,α^*,β^*) p∗=d∗=L(x∗,α∗,β∗)
定理3: 在满足定理2的条件下,则 x ∗ , α ∗ , β ∗ x^*,α^*,β^* x∗,α∗,β∗分别是原始问题和对偶问题的最优解的充要条件是 x ∗ , α ∗ , β ∗ x^*,α^*,β^* x∗,α∗,β∗满足下面的KTT条件:
(1) ∇ x L ( x ∗ , α ∗ , β ∗ ) = 0 ∇_xL(x^*,α^*,β^*) = 0\tag{1} ∇xL(x∗,α∗,β∗)=0(1)
(2) α ∗ c i ( x ) = 0 , i = 1 , 2 , . . . , k α^*c_i(x)=0, \quad i=1,2,...,k\tag{2} α∗ci(x)=0,i=1,2,...,k(2)
(3) c i ( x ) ≤ 0 , i = 1 , 2 , . . . , k c_i(x)\leq0, \quad i=1,2,...,k\tag{3} ci(x)≤0,i=1,2,...,k(3)
(4) α i ≥ 0 , i = 1 , 2 , . . . , k α_i\geq0, \quad i=1,2,...,k\tag{4} αi≥0,i=1,2,...,k(4)
(5) h j ( x ∗ ) = 0 j = 1 , 2 , . . , l h_j(x^*)=0 \quad j=1,2,..,l\tag{5} hj(x∗)=0j=1,2,..,l(5)
其中条件(1)是指函数对于 x ∗ , α ∗ , β ∗ x^*,α^*,β^* x∗,α∗,β∗偏导为0,(3~5)是约束条件.
并且注意条件(4),当 α i > 0 α_i > 0 αi>0(注意只是大于而不是大于等于,原条件中是大于等于),则由条件(2)(3)可知 c i ( x ) = 0 c_i(x)=0 ci(x)=0.
参考
https://www.cnblogs.com/xinchen1111/p/8804858.html
https://www.cnblogs.com/90zeng/p/Lagrange_duality.html
http://blog.pluskid.org/?p=702
<统计学习方法> 李航
