leetcode459奇妙做法的数学解释

前言

前几天做了下leetcode459，这道看起来平淡无奇的题目，却是如此的好玩。我们经常看网上一些人写的题解，粗暴，直接上代码，然后唯一的中文是“水题，不解释”，科科哒，港真，有多少人知道其数学原理，反正我是不建议轻视每一个我们碰到的问题。

首先，回顾一下问题：

简单的说，就是判断一个字符串是否能完全被自身一个子串多次拼接得到。比如“ababab”可以由“ab”拼接而成（我们称之为“好串”），“ababc”则不存在一个子串能拼接出原字符串。

碰到问题，暴力先行，我们可以简单地给出一种暴力的方法：

class Solution:
    def repeatedSubstringPattern(self, s):
        """
        :type s: str
        :rtype: bool
        """
        for x in range(int(len(s)/2)):
            temp=s[0:(x+1)]
            times=int(len(s)/(x+1))
            if temp*times==s:
                return True
        return False      

实际上就是遍历 s ，看前 x 个字符构成的子串能不能拼接出 s ，这样的暴力是 O(n2) ，当然如果在做代码中if语句之前，判断一下times是否能被len(s)整除的话，可以降到 O(rn) ，其中 r 为 n 的约数的个数，不过这样的改进似乎没有起到很大的作用，因为在我之前的博客《leetcode483. Smallest Good Base 的一些思考 》中讨论了一个不大于n的正整数的约数个数期望意义下是多少的问题，结论是大约为 O(logn) ，于是这样微小的改进大约是 O(nlogn) ，还过得去，聊胜于无~

然后，标答的话，应该是采用 O(n) 的KMP算法，在本文中不做详细介绍，或者了留个微小的坑（立个flag），最近（其实是懒）有点忙。然后，在浏览discuss时候，发现了有个非常非常神奇的做法，给出代码如下：

class Solution:
    def repeatedSubstringPattern(self, s):
        return s in (2 * s)[1:-1]

是的，就是一行，这里剧透一下，这是 O(n) 的算法，简单地说，这个算法分为如下几步：

（算法1）
1. 用两个 s 首尾相连得到一个新的字符串 ss ;
2. 去掉 ss 的首尾两个字符；
3. 如果在剩下来的字符串中能找到 s 那么返回True，否则False

实在是惊人，经过一段时间的思考，终于给出了这个方法的证明，在这个过程中想到了很多东西，非常兴奋，兴奋得我跑去清青快餐吃了一波，然后下面的话，我将会给出我的完整的思考过程（和以前一样，我认为记录思考过程比记录冷冰冰的证明要有意义得多，或者你可以直接拖到后面看证明）

思考过程

如图所示， s1 和 s2 分别为步骤1中所给出的两个字符串

记序列 s1s2 的字符分别为 a0 ， a1 ，…， a2n−1 ，若在 s1s2 去掉首尾后中能找到 s1(s2) 的话，也就是说存在 k 使得 (a0a1...an−1)=(akak+1...ak+n−1)=(anan+1...a2n−1) ，其中 1≤k≤n−2 ，于是我们马上有：（ 0≤t≤n−1 ）

⎧⎩⎨⎪⎪at=at+nat=at+kat=at+n−k,

为了方便起见，上式中的下标是mod n意义下的，换句话说 {an} 有三个周期，分别是 n , k , n−k ，但是实际上由于是mod n意义下，于是周期 n−k 和 k 是相同的，此时，我猜想：

（猜想1）若有 at=at+n 以及 at=at+k ， k≤n ，那么一定存在一个 r|n ，使得 at=at+r.

如果猜想1成立，那么我们就可以判定，算法1可以用来判断“好串”（ (a0a1...ar−1) 能生成整个原字符串），不妨加强一下猜想1，做一个更加具体的猜想：

（猜想2）若有 at=at+n 以及 at=at+k ， k≤n ，那么 at=at+gcd(k,n) .

此时，我做了一些实验，下面展示一些例子(不断+4然后取模6)，
1. k=4,n=6 ，如图所示

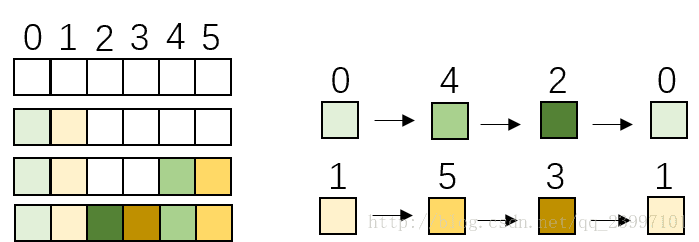
上图中颜色相近的表示的是值相同（颜色深浅是为了方便读者阅读），实际上就是下图中的好串，它确实有周期 gcd(4,6)=2 ，而且字符串被分为 gcd(n,k) 种等价类（绿色和黄色）。

有了上述实验后，我再做了一个尝试（直觉告诉我不妨做个互质情况的实验）

2. k=4,n=5

很高兴，和我的猜想一致，它确实有 gcd(4,5)=1 的周期，以及字符串被分为 gcd(n,k) 种等价类（蓝色）。我想，如果把上两幅图的操作看成是一种变换（上面两幅图右边的箭头），那么序列只有在 gcd(k,n)=1 的时候，变换才能遍历整个字符串中的每一个元，否则早早就进入循环了。

重新再以 k=4,n=6 为例，实际上，这个变换就是不断+4然后取模6的过程，那么我想，能不能证明对于任意的等差数列 ak+t ，对于任意 n>1 ，取mod n后都会变成周期数列，

此时我突然想到一些东西，我印象中好像有这么一个定理：

（定理1）对于常系数齐次线性递推公式 an+k=∑ki=1ckan+i−1 ，若 m>1 ，那么数列 {an} 模 m 后是周期数列.

我能不能将等差数列转换为常系数齐次线性递推公式，然后通过定理1的某些性质来直接证明猜想2呢？先来看看， ak+t 的话，似乎可以有

(a+1)k+t=2(ak+t)−[(a−1)k+t],

也就是说，我们有 Aa+1=2Aa−Aa−1 ，棒！还真的可以转换为常系数齐次线性递推公式，等等， Aa+1=2Aa−Aa−1 的特征方程是 x2−2x+1=(x−1)2 ，我去，对了，二次的特征方程，且有两个重根的通项公式就是一次函数！也就是等差数列！棒极了！周期性用抽屉原理就可以证明，好像直接从等差数列角度也能直接证明，化为递推公式好像没卵用（囧），而且好像没有查到关于定理1的一些有关的好性质，没劲，好像又回到了原点，看看自己能不能解决猜想2.

完整证明

回顾一下，由已知存在 k （ 1≤k≤n−2 ），我们有：（ 0≤t≤n−1 ）

{at=at+nat=at+k,

我们只要证明猜想2，我们就能说明算法1给出True的判断就是好串，False的结果必然是非好串。这主要是因为 gcd(n,k)|n ， (a0a1...agcd(n,k)−1) 能生成整个原字符串.

（猜想2）若有 at=at+n 以及 at=at+k ， k≤n ，那么 at=at+gcd(k,n) .

下面我们来证明猜想2，首先我们有如下引理：

（引理1）用 lcm(m,k) 和 gcd(m,k) 来表示 m,k 的最小公倍数和最大公约数，那么我们有 lcm(m,k)⋅gcd(m,k)=mk .

接下来给出关于一次线性同余方程解得存在性定理：

（引理2：线性同余式定理）设 a,b,m∈N+ ，给定一次同余方程 ax≡b(modm) ，
（1）若 gcd(a,m)|b ，那么同余方程有 gcd(a,m) 个在模 m 的不同解，如果有特解 x0 ，那么全部解得形式为 x=x0+t⋅m/gcd(a,m) ， t=0,1,...,gcd(a,m)−1 ；
（2）若不整除，那么同余方程不存在解.

我们考虑序列下标序列 t,t+k,t+2k,t+3k... 即 ak+t ，

（第一步）我们先证明：

a⋅k+t≡(a+ngcd(k,n))k+t(modn),

这等价于 kn/gcd(k,n)≡0(modn) ，由引理1有 kn/gcd(k,n)=lcm(k,n) ，于是，最小公倍数 lcm(k,n) 当然可以整除 n ，于是马上知道，上式成立。

（第二步）接下来，固定 t ，我们证明对于 ak+t ， a 从0取到 ngcd(k,n)−1 这 ngcd(k,n) 个数，在模 n 的意义下互不相同，反设，存在 p,q ， 0≤p<q≤ngcd(k,n) ，使得 pk+t≡qk+t(modn) ，那么我们有 k(p−q)≡0(modn) ，注意到此时有:

k⋅(p−q)<k⋅ngcd(k,n)=lcm(k,n),

若有 k(p−q)≡0(modn) ，这与最小公倍数 lcm(k,n) 的最小性矛盾！

回到原猜想2（再次重申，所有的下标就是模 n 意义下的），由第一步和第二步，我们知道，对于原字符串 a1,a2,...,an−1 中，取定一个 t ，必有：

at=at+k=at+2k=...=at+ngcd(k,n)−1,

上式中的元构成的集合我们称为等价类 At⊂s ，下面我们证明等价类 At⊂s 中的元，下标必是 gcd(k,n) 为周期，用数学的语言描述即任取一个元 at+kx∈At ，必有 at+kx+gcd(k,n)∈At ， 0≤x≤ngcd(k,n)−1 .直接证明，似乎没那么容易，换一个角度，我是否能 构造一个集合 A′t 使得：

• A′t 中的元有 at+p⋅gcd(k,n) 的形式（ 0≤p≤ngcd(k,n)−1 ）；
• 存在双射 f : A′t→At .

这样的话 A′t 与 At 的元完全相同，而 A′t 的元的下标是以 gcd(k,n) 为周期的，那么 At 也必是如此！

取定 p∈[0,ngcd(k,n)−1] ，考察同余方程

x⋅k+t≡p⋅gcd(k,n)+t(modn),

在 [0,ngcd(k,n)−1] 上的正整数解。由引理2（线性同余式定理），因为 gcd(k,n)|p⋅gcd(k,n) ，故同余方程有 x=x0+t⋅n/gcd(a,n) ， t=0,1,...,gcd(a,n)−1 ，由抽屉原理，不管 x0 是什么，在模 n 的意义下，上述同余方程在 [0,ngcd(k,n)−1] 有唯一解！（因为解步长是 ngcd(k,n) ），

同理，取定 a∈[0,ngcd(k,n)−1] ，考察同余方程

a⋅k+t≡x⋅gcd(k,n)+t(modn),

在 [0,ngcd(k,n)−1] 上有唯一解！

所以上面两个同余方程的解唯一性保证了 A′t 和 At 的元是一一对应的，于是 At 的元在模 n 的意义下必是以 gcd(k,n) 为周期的。即对于任意的 t ，都有 at=at+gcd(k,n) ，故完成证明！

————————————————

后记

由上面的思考，顺便得到如下结论：

（结论1）对等差数列 ak+t ， a∈N+ ，取mod n后所得到的周期数列，必有周期 n/gcd(k,n) ，且 n/gcd(k,n) 为最小正周期.

修改一下结论1有：

（结论2）常系数齐次线性递推公式 Aa+1=2Aa−Aa−1 取mod n后所得到的周期数列的周期完全取决于初值.

进一步的思考：

（作业）若有 at=at+ki ，其中 i=1,2...n ，那么是否有 at=at+gcd(k1,k2,...,kn)? .

如果，上面的这个作业成立的话，那么由之前我的这篇博文:从Happy num所想到的几个问题 最后提到任取k个自然数，它们互素的概率为 1ζ(k) ，即有非常大的概率，使得数列 {at} 每一项都是相同的.