稀疏表示

1.  问题背景

 

        信号的稀疏表示并不是新的东西。我们很早就一直在利用这一特性。例如，最简单的JPEG图像压缩算法。原始的图像信号经过DCT变换之后，只有极少数元素是非零的，而大部分元素都等于零或者说接近于零。这就是信号的稀疏性。

        任何模型都有建模的假设条件。压缩感知，正是利用的信号的稀疏性这个假设。对于我们处理的信号，时域上本身就具有稀疏性的信号是很少的。但是，我们总能找到某种变换，使得在某个变换域之后信号具有稀疏性。这种变换是很多的，最常见的就是DCT变换，小波变换，gabor变换等。

        然而，这种正交变换是传统视频图像处理采用的方法。目前所采用的一般不是正交变换。它是基于样本采样的。或者说是通过大量图像数据学习得到的，其结果称作字典，字典中的每一个元素称作原子。相关的学习算法称作字典学习。常见的算法例如K-SVD算法。学习的目标函数是找到所有样本在这些原子的线性组合表示下是稀疏的，即同时估计字典和稀疏表示的系数这两个目标。

 

       压缩感知和稀疏表示其实是有些不同的。压缩感知的字典是固定的，在压缩感知的术语里面其字典叫做测量矩阵。但压缩感知的恢复算法和稀疏表示是同一个问题。他们都可以归结为带约束条件的L1范数最小化问题。求解这类泛函的优化有很多种方法。早在80年代，统计学中Lasso问题，其实和稀疏分解的优化目标泛函是等价的。而求解统计学中lasso 问题的LARS算法很早就被提出了，故我们还可以通过统计学的LARS算法求解稀疏表示问题。目前很多统计学软件包都自带LARS算法的求解器。

 

2. 基于稀疏表示的分类 SRC

 

      人脸的稀疏表示是基于光照模型。即一张人脸图像，可以用数据库中同一个人所有的人脸图像的线性组合表示。而对于数据库中其它人的脸，其线性组合的系数理论上为零。由于数据库中一般有很多个不同的人脸的多张图像，如果把数据库中所有的图像的线性组合来表示这张给定的测试人脸，其系数向量是稀疏的。因为除了这张和同一个人的人脸的图像组合系数不为零外，其它的系数都为零。

       上述模型导出了基于稀疏表示的另外一个很强的假设条件：所有的人脸图像必须是事先严格对齐的。否则，稀疏性很难满足。换言之，对于表情变化，姿态角度变化的人脸都不满足稀疏性这个假设。所以，经典的稀疏脸方法很难用于真实的应用场景。

       稀疏脸很强的地方在于对噪声相当鲁棒，相关文献表明，即使人脸图像被80%的随机噪声干扰，仍然能够得到很高的识别率。稀疏脸另外一个很强的地方在于对于部分遮挡的情况，例如戴围巾，戴眼镜等，仍然能够保持较高的识别性能。上述两点，是其它任何传统的人脸识别方法所不具有的。

 

3. 稀疏人脸识别的实现问题

 

        一谈到识别问题，大家都会想到要用机器学习的方法。先进行训练，把训练的结果以模板的形式存储到数据库上；真实应用环境的时候，把测试样本经过特征提取之后，和数据库中的模板进行比对，查询得到一个最相似的类别作为识别结果。往往，机器训练的时间都超级长，几天，几个礼拜乃至几个月，那是常见的事情；识别的时间一般是很小的。典型的例如人脸检测问题。这是可以接受的，因为训练一般都是离线的。

 

        然而，基于稀疏分解的人脸识别是不需要训练的，或者说训练及其简单。基于稀疏表示的人脸识别，其稀疏表示用的字典直接由训练所用的全部图像构成，而不需要经过字典学习【也有一些改进算法，针对字典进行学习的】。当然，一般是经过简单的特征提取。由于稀疏表示的方法对使用什么特征并不敏感。故而，其训练过程只需要把原始图像数据经过简单的处理之后排列成一个很大的三维矩阵存储到数据库里面就可以了。

 

        关键的问题在于，当实际环境中来了一张人脸图像之后，去求解这张人脸图像在数据库所有图像上的稀疏表示，这个求解算法，一般比较耗时。尽管有很多的方法被提出，但是对于实时应用问题，依然没法满足。所以，问题的关键还是归结于L1范数最小化问题上来。

 

       L1范数最小化问题已经有很多种快速求解方法，这里主要包括有梯度投影Gradient Projection,同伦算法，迭代阈值收缩，领域梯度Proximal Gradient，增广拉格朗日方法，这几种方法都比正交匹配追踪算法OMP要高效的多。上述几种快速算法中，采用增广拉格朗日的对偶实现相比其它的快速算法要更好。最近流行的Spit Bregman算法也是不错的选择。

      

4. 稀疏表示人脸识别的改进算法

 

         稀疏人脸识别算法要用于实际的系统，需要在两方面加以改进。首先，要突破人脸图像的对齐这一很强的假设。实际环境中的人脸往往是不对齐的，如何处理不对其的人脸是额待解决的问题。其实，是快速高效的优化算法。最后，也是最重要，实际环境中的应用往往训练样本很少。目前，研究人员已经取得了很多可喜的成果，下面分别予以介绍。

 

4.1 CRC-RLS算法 

         CVPR2011 LeiZhang  Sparse Representatiion or Callaborative Representation: Which helps Face Recognition? 稀疏表示和协同表示，哪一个有助于人脸识别。该文作 者提出了用L2范数代替L1范数求解原问题。这样，能够非常快速的求解问题，实时性没有任何问题。但稀疏性不像原来的L1范数那样强。但作者对分类准则进行了改进，使得其分类性能几乎接近于原始L1范数最小化问题分类性能。为了对比，我把关键性算法列表如下：

 

                                           

                                         

         SRC算法求解的是方程1的解，而CRC-RLS算法则直接给出了表示系数的最小二乘解。二者另外一个主要的不同点在于计算残差的方式不一样，具体请注意上述方程2和方程10的不同点。后者的计算时间较前者最多情况下加速了1600倍。更多的实现细节可以参考原文。

       

   4.2  RSC算法 

              CVPR2011 Meng Yang，Robost  Sparse Coding for Face Recognition. 鲁棒的稀疏编码算法。该文作者没有直接求解稀疏编码问题，而是求解Lasso问题，因为Lasso问题的解和稀疏编码的解是等价的。在传统的SRC框架下，编码误差使用L2范数来度量的，这也就意味着编码误差满足高斯分布，然而，当人脸图像出现遮挡和噪声污染的情况下，并非如此。在字典学习框架下，这样的字典是有噪声的。该文作者对原始Lasso问题进行改进，求解加权L1范数约束的线性回归问题。Lasso问题描述如下：

 

                                    

 

               加权Lasso问题的目标函数描述如下：

                                                             

            此算法的关键还在于权重系数的确定，文中采用的是logistic函数，而具体的实现则是通过迭代估计学习得到。该方法基于这样一个事实：被遮挡或噪声干扰的像素点赋予较小的权重，而其它像素点的权重相对较大。具体迭代算法采用经典的迭代重加权算法框架，当然内部嵌入的稀疏编码的求解过程。此算法在50%遮挡面积的情况下取得的更好更满意的结果。但是文中没有比较计算时间上的优略而直说和SRC框架差不多。

 

4.3  RASL算法

        CVPR2010. Yigang Peng.  Robust batch Alignment of Images by Sparse and Low-Rank Decomposition. 这篇文章的作者在这篇文章中讨论的是用矩阵的低秩分解和稀疏表示来对齐人脸的问题。

 

4.4  RASR算法

       PAMI2011 Wagner. Towards a Practical Face Recognition System：Robust Alignment and Illumination by Sparse Representation.该文的目的和RASL类似。

 

4.5  MRR算法

          ECCV2012，Meng Yang. Efficient Misalignment-Robust Representation for Real Time Face Recognition.这篇文章又是Meng Yang的大作。这篇文章在充分分析RASR算法的基础上提出了一个高效的快速算法。该文对人脸对齐中求解变换矩阵T分为由粗到细的两个阶段。 这篇文章把稀疏脸应用在实际系统中推进了一大步。具体算法实现本人正在拜读之中。

 

        对稀疏脸的改进算法其实很多，例如分块SRC算法，表情鲁棒SRC等。但本人认为能够把它推向实际应用的却很少。上述文献是本人认为可圈可点的值得仔细拜读的文献

 

 

1.提出问题：什么是稀疏表示 
假设我们用一个M*N的矩阵表示数据集X，每一行代表一个样本，每一列代表样本的一个属性，一般而言，该矩阵是稠密的，即大多数元素不为0。 
稀疏表示的含义是，寻找一个系数矩阵A（K*N）以及一个字典矩阵B（M*K），使得B*A尽可能的还原X，且A尽可能的稀疏。A便是X的稀疏表示。 
书上原文为（将一个大矩阵变成两个小矩阵，而达到压缩）

“为普通稠密表达的样本找到合适的字典，将样本转化为合适的稀疏表达形式，从而使学习任务得以简化，模型复杂度得以降低，通常称为‘字典学习’（dictionary learning），亦称‘稀疏编码’（sparse coding）”块内容

表达为优化问题的话，字典学习的最简单形式为： 

其中xi为第i个样本，B为字典矩阵，aphai为xi的稀疏表示，lambda为大于0参数。 
上式中第一个累加项说明了字典学习的第一个目标是字典矩阵与稀疏表示的线性组合尽可能的还原样本；第二个累加项说明了alphai应该尽可能的稀疏。之所以用L1范式是因为L1范式正则化更容易获得稀疏解。具体原因参看该书11.4章或移步机器学习中的范数规则化之（一）L0、L1与L2范数。字典学习便是学习出满足上述最优化问题的字典B以及样本的稀疏表示A（A{alpha1，alpha2，…，alphai}）。L1正则化常用于稀疏，可以获得稀疏解。如下图表示，L1正则化交点在轴上，所得的解一般只是在某个轴上有实数，另外的轴为0，从而最终得到稀疏解。

2.字典学习求解 （学习字典、稀疏表示）
求解上述最优化问题的总体策略是，对字典B以及样本稀疏表示alphai交替迭代优化。即先初始化字典B，

1.固定字典B对alphai进行优化。2.固定A对字典B进行优化。重复上述两步，求得最终B以及X的稀疏表示A。 
其中第一步可采用与LASSO正则化相似的方法（如Proximal Gradient Desent法）进行求解，第二步可采用KSVD方法进行求解。具体步骤参看该书11.5章节内容

 

1. 之前虽然听过压缩感知和稀疏表示，实际上昨天才正式着手开始了解，纯属新手，如有错误，敬请指出，共同进步。

2. 主要学习资料是 Coursera 上 Duke 大学的公开课——Image and video processing, by Pro.Guillermo Sapiro 第 9 课。

3. 由于对图像处理的了解也来自与该课程，没正经儿看过几本图像方面的书籍，有些术语只能用视频中的英文来表达，见谅哈！

 

1. Denoising 与 MAP

故事从 denoising 说起，话说手头上有一张含有噪音的图片 Lena，如何除去噪音得到好的 clean image 呢？

对于上面的问题，用 x 值表示某个像素的灰度值，我们可以建立这样一个最小化的数学模型：

其中， y 表示已知的观测值，也就是含有噪声的原图， x 表示要恢复成 clean image 的未知值。

模型的第一项的直观作用就是，预测值 x 不要离观测值 y 太远。数学上的解释是， x 的取值概率可以看做是以 y 为均值的高斯分布，即图像带有 Gaussian noise， 第二项是规则化项。由来如下：假设 x 本来是就带有某种先验概率的分布，现在又已知观测值 y， 根据贝叶斯原理， 现在 x 的分布（后验）正比于先验概率分布与高斯分布的乘积。如果先验概率分布也正是指数分布，将乘积取负对数，就可以得到上述在机器学习里非常常见的 MAP 模型。

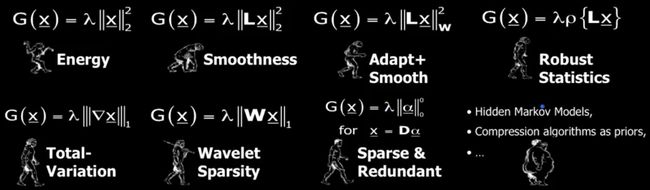
现在的问题是：最好的先验 (prior) 究竟是什么？ G(x) 应该取什么形式？ 定义图像信号的最好空间是什么？

在学术界，这方面的工作已经做得非常多，对这个问题的探讨过程可以比喻成类人猿向人类进化的过程:

第一张图， prior 假设 clean image 能量尽量小， x 要尽可能地小。第二张图， prior 认为恢复后的图像要光滑，于是产生了 Laplacian 和 low energy 的结合，朝前进化了一步。第三张图，prior 认为要考虑 edges 是不光滑滴，需要不同情况不同处理…… Sparse and Redundant 是正在讨论的问题，目前是最新的进化版本，而后面也有一些算法，虽然也成功进化成人类，可惜太胖了，行动不便—— computationally expensive and difficult。 Sparse modeling 的先验究竟是什么？要回答这个问题，还需要了解一些基础概念。

 

2. Sparsity and Lp Norm

1. How to Represent Sparsity

   表示一个向量的稀疏程度可以用 Lp norm， 对于 alpha 向量的某一个元素为 x， Lp norm 的计算公式和函数图像如下：

   

   我们希望不管 x 多大，它非零的惩罚是相同的，L0 norm 正好满足这个要求，它表示的意思是数出 alpha 向量中非零的个数。

2. Sparse Modeling of Signal

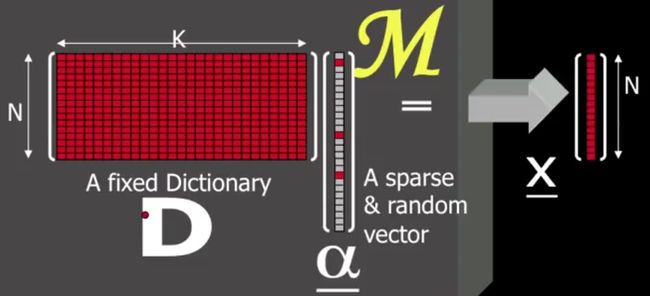
   一张 8×8 的图片，可以表示成 64 维的向量 x ，如何进行稀疏表示？下图中假设 N = 64：

   

   左边矩阵 D 是字典矩阵，由 K 个 N 维的列向量组成。 根据 K 与 N 的关系，又可以划分为：

   1. K > N: over-complete, 这种情况在稀疏表示里面最常见

   2. K = N: complete, 例如傅里叶变换和 DCT 变换都是这种情况

   3. K < N: under-complete

 

中间列向量 alpha 是一个稀疏向量，特点是非零项很少，图中只有三个非零项，代表 D 矩阵对应行向量的线性组合。

最后 x 向量表示恢复后的向量。

atoms 表示 D 的列向量

实际上 DCT 变换也可以看做是一种稀疏表示，它的 D 向量是由固定的且刚好完备的正交基向量组成，并且 alpha 向量也具有一定稀疏性。

对于上图，假设 D 矩阵 K > N，并且是满秩的，那么对于任意个 N 维的向量 b （图中是 x ），肯定有 Ax = b。现在加入 Lp norm 的约束条件，限制只能用少量的 A 的列向量 (atoms 作为基，向量 b 就被固定在某个 span 内，成为了一个 Lp 优化问题：

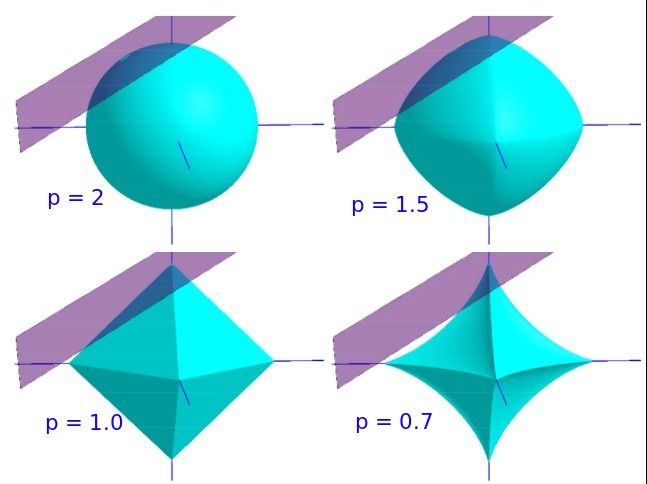
用紫色表示平面，用青色表示 norm 取同一个值的球形(等高线)，问题如下：在平面 Ax = b 平面内选出 norm 最小的最优解

当 p >= 1时，norm ball和平面的交点有多个。这是一个凸优化问题，可以用拉格朗日乘子来解决这个问题。

当 0 < p < 1 时， norm ball 可行解十分稀疏，是一个非凸优化问题，解决这类问题很难，但是却有很好的稀疏性。

当 p = 0 时， norm ball 上的点除了坐标轴，其他部分无限收缩，与平面的交点在某一个坐标轴上，非零系数只有一个。

回到第一节将的 MAP 模型， Sparse Modeling 模型就是非零系数限制在 L 个之内（意味着解在至多 L 个 atoms 组成的 span 里），尽可能接近平面:

这样，我们用少量的 atoms 组合成真实信号，而 noise cannot be fitted very well, 在投影到低维空间的过程中起到了降噪的作用。 

 

 

3. Some Issues：

 模型可以改成 L0 norm 的形式和其他形式来计算或者求近似吗？

解集 alpha 向量是唯一的吗？我们可以求它的近似吗？如果可以，如何估计近似程度?

应该采用什么样的字典矩阵 D 才能较好地消除噪声？字典 D 如何确定？