机器学习算法2(用python实现三种梯度下降)
用python实现三种梯度下降
我尽量详细的进行相关注释
代码如下
import numpy as np #导入numpy
import os #导入os操作系统
# 画图
%matplotlib inline
import matplotlib.pyplot as plt
# 随机种子,用随机函数时自动触发
np.random.seed(42)
# 保存图像
PROJECT_ROOT_DIR = "." #将数据用点的形式呈现
MODEL_ID = "linear_models"
#注意,在本文档的同级目录下创建文件夹“images”,然后在“images”里面创建文件夹“linear_models”。保持命名一致
#定义一个保存图像的函数
def save_fig(fig_id, tight_layout=True):
#指定保存图像的路径 当前目录下的images文件夹下的model_id文件夹
path = os.path.join(PROJECT_ROOT_DIR, "images", MODEL_ID, fig_id + ".png")
#提示函数,正在保存图片
print("Saving figure", fig_id)
#保存图片(需要指定保存路径,保存格式,清晰度)
plt.savefig(path, format='png', dpi=300)
# './images/linear_models/xx.png'
# 把讨厌的警告信息过滤(忽略)掉
import warnings
warnings.filterwarnings(action="ignore")
X = 2 * np.random.rand(100, 1) # 生成训练数据(特征部分)
y = 4 + 3 * X + np.random.randn(100, 1) #生成训练数据(标签部分)
plt.plot(X, y, "b.") #画图
plt.xlabel("$x_1$", fontsize=18) #x轴标签
plt.ylabel("$y$", rotation=0, fontsize=18) #y轴标签
plt.axis([0, 2, 0, 15]) #指定x轴起始位置和单位距离,y轴起始位置和单位距离
save_fig("generated_data_plot") #保存图片
plt.show() #展示
# 添加新特征(这是一个我刚get到的添加数组的方式)
X_b = np.c_[np.ones((100, 1)), X]
# 创建测试数据
X_new = np.array([[0], [2]])
X_new_b = np.c_[np.ones((2, 1)), X_new]
#从sklearn包里导入线性回归模型
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression() #创建线性回归对象
lin_reg.fit(X, y) #拟合训练数据
lin_reg.intercept_, lin_reg.coef_ #输出截距,斜率
lin_reg.predict(X_new) #对测试集进行预测
批量梯度下降
eta = 0.1 #指定梯度下降的步长
n_iterations = 1000 #指定梯度下降的迭代次数
m = 100 #指定数据集数
theta = np.random.randn(2,1) #生成一列两行的矩阵
for iteration in range(n_iterations):# 限定迭代次数
gradients = 2/m * X_b.T.dot(X_b.dot(theta) - y)
#a dot b 表示矩阵a乘以矩阵b
# a.T 表示 矩阵a的转置
theta = theta - eta * gradients #更新theta
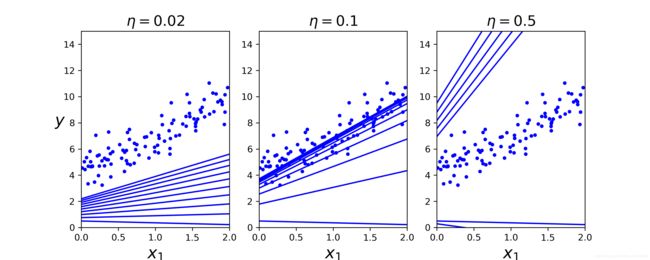
def plot_gradient_descent(theta, eta, theta_path=None):
m = len(X_b)
plt.plot(X, y, "b.")
n_iterations = 1000
for iteration in range(n_iterations):
if iteration < 10:
y_predict = X_new_b.dot(theta)
style = "b-"
plt.plot(X_new, y_predict, style)
gradients = 2/m * X_b.T.dot(X_b.dot(theta) - y)
theta = theta - eta * gradients
if theta_path is not None:
theta_path.append(theta)
plt.xlabel("$x_1$", fontsize=18)
plt.axis([0, 2, 0, 15])
plt.title(r"$\eta = {}$".format(eta), fontsize=16)
np.random.seed(42)
theta = np.random.randn(2,1)
plt.figure(figsize=(10,4))
plt.subplot(131); plot_gradient_descent(theta, eta=0.02)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.subplot(132); plot_gradient_descent(theta, eta=0.1, theta_path=theta_path_bgd)
plt.subplot(133); plot_gradient_descent(theta, eta=0.5)
save_fig("gradient_descent_plot")
plt.show()
随机梯度下降
theta_path_sgd = []
m = len(X_b)
np.random.seed(42)
n_epochs = 50
theta = np.random.randn(2,1) # 随机初始化
for epoch in range(n_epochs):
for i in range(m):
if epoch == 0 and i < 20:
y_predict = X_new_b.dot(theta)
style = "b-"
plt.plot(X_new, y_predict, style)
# random_index = np.random.randint(m)
xi = X_b[i:i+1]
yi = y[i:i+1]
gradients = 2 * xi.T.dot(xi.dot(theta) - yi)
eta = 0.1
theta = theta - eta * gradients
theta_path_sgd.append(theta)
plt.plot(X, y, "b.")
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.axis([0, 2, 0, 15])
save_fig("sgd_plot")
plt.show()
from sklearn.linear_model import SGDRegressor
sgd_reg = SGDRegressor(max_iter=1000, tol=-np.infty, penalty=None, eta0=0.1, random_state=42)
sgd_reg.fit(X, y.ravel())
sgd_reg.intercept_, sgd_reg.coef_
小批量梯度下降
theta_path_mgd = []
n_iterations = 50
minibatch_size = 20
np.random.seed(42)
theta = np.random.randn(2,1) # random initialization
for epoch in range(n_iterations):
shuffled_indices = np.random.permutation(m)
X_b_shuffled = X_b[shuffled_indices]
y_shuffled = y[shuffled_indices]
for i in range(0, m, minibatch_size):
xi = X_b_shuffled[i:i+minibatch_size]
yi = y_shuffled[i:i+minibatch_size]
gradients = 2/minibatch_size * xi.T.dot(xi.dot(theta) - yi)
eta = 0.1
theta = theta - eta * gradients
theta_path_mgd.append(theta)
theta_path_bgd = np.array(theta_path_bgd)
theta_path_sgd = np.array(theta_path_sgd)
theta_path_mgd = np.array(theta_path_mgd)
plt.figure(figsize=(7,4))
plt.plot(theta_path_sgd[:, 0], theta_path_sgd[:, 1], "r-s", linewidth=1, label="Stochastic")
plt.plot(theta_path_mgd[:, 0], theta_path_mgd[:, 1], "g-+", linewidth=2, label="Mini-batch")
plt.plot(theta_path_bgd[:, 0], theta_path_bgd[:, 1], "b-o", linewidth=3, label="Batch")
plt.legend(loc="upper left", fontsize=16)
plt.xlabel(r"$\theta_0$", fontsize=20)
plt.ylabel(r"$\theta_1$ ", fontsize=20, rotation=0)
plt.axis([2.5, 4.5, 2.3, 3.9])
save_fig("gradient_descent_paths_plot")
plt.show()