【数学】约束优化方法:拉格朗日乘子法 与 KKT条件
拉格朗日乘子法与KKT条件
引言
约束条件可分为等式约束和不等式约束。如果是等式约束,可以直接利用拉格朗日乘子法(Lagrange Multiplier)求解最优值。对于不等式约束,可以转化为满足 KKT(Karush-Kuhn-Tucker) 条件后再利用拉格朗日乘子法求解。但是在一般情况下,这两个方法求得的结果只是必要条件,也就是可行解。而当目标函数是凸函数的情况下,才是充分必要条件,求得最优解。
无约束优化
假设存在 f ( x ) f(x) f(x) 是定义在 R n R^n Rn 上的连续可微函数,考虑无约束优化,求: min x f ( x ) \min_xf(x) xminf(x)
我们可以直接使它导数为 0 0 0 即可。
等式约束优化
原始问题
假设存在 f ( x ) , h i ( x ) f(x), h_i(x) f(x),hi(x) 是定义在 R n R^n Rn 上的连续可微函数,考虑等式优化,求: min x f ( x ) s . t . h i ( x ) = 0 , i = 1 , 2 , 3 , … , m \min_xf(x)\\ s.t.\ \ \ \ h_i(x) = 0,i=1,2,3,\dots,m xminf(x)s.t. hi(x)=0,i=1,2,3,…,m
( s . t . s.t. s.t. 是 s u b j e c t t o subject\ to subject to 的缩写,意为“受限于”,表示约束条件)
其中, h i ( x ) = 0 h_i(x) = 0 hi(x)=0 表示存在 m m m 条形如 h ( x ) = 0 h(x) = 0 h(x)=0 的这种约束条件。
有等式约束条件的情况下,会把解限定在一个可行域内,即同时满足所有约束条件。
求解
我们尝试去理解利用约束函数和目标函数的法向量平行的性质去解决问题:这个链接

我们用拉格朗日乘子法构造拉格朗日函数:
L ( x , α ) = f ( x ) + ∑ i = 1 m α i h i ( x ) \mathscr{L}(x,\alpha)=f(x) + \sum_{i=1}^m\alpha_ih_i(x) L(x,α)=f(x)+i=1∑mαihi(x)
其中 α i \alpha_i αi 就是拉格朗日乘子。
因此我们可以得到:
{ ∂ L ( x , α ) ∂ x = 0 ∂ L ( x , α ) ∂ α = 0 \begin{cases}\\ {\partial\mathscr{L}(x,\alpha)\over \partial x} = 0\\ {\partial\mathscr{L}(x,\alpha)\over \partial\alpha} = 0\\ \end{cases} {∂x∂L(x,α)=0∂α∂L(x,α)=0
联立以上方程,求解出 x x x,即是目标函数满足等式约束关系的可行解。
由上可以看出,拉格朗日乘子法,可以将带有约束关系的原始问题,简化为没有约束关系的拉格朗日函数,最后求解拉格朗日函数即可。
不等式优化约束
原始问题
假设存在 f ( x ) , g i ( x ) f(x),g_i(x) f(x),gi(x) 是定义在 R n R^n Rn 上的连续可微函数,考虑不等式约束优化,求:
min x ∈ R n f ( x ) s . t . g i ( x ) ≤ 0 , i = 1 , 2 , 3 , … , k \min_{x\in R^n}f(x)\\ s.t.\ \ \ \ g_i(x) \leq 0,\ i=1,2,3,\dots,k x∈Rnminf(x)s.t. gi(x)≤0, i=1,2,3,…,k
其中 g i ( x ) ≤ 0 g_i(x) \leq 0 gi(x)≤0 表示存在 k k k 条形如 g ( x ) ≤ 0 g(x) \leq 0 g(x)≤0 的这种约束条件。
求解
有不等式约束条件的情况下,会把解限定在一个可行域内,即同时满足所有约束条件。目标函数的等高线和约束区域如图:
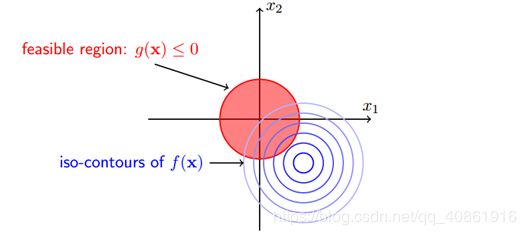
显然,可行解 x x x 只能在 g ( x ) ≠ 0 g(x) \neq 0 g(x)̸=0 取得:
1. 当可行解满足 g ( x ) < 0 g(x) < 0 g(x)<0,此时极小化 f ( x ) f(x) f(x) 即可。
2. 当可行解满足 g ( x ) = 0 g(x)=0 g(x)=0, 此时等价于等式约束条件。
同样,我们也对约束关系构造拉格朗日函数:
L ( x , β ) = f ( x ) + ∑ i = 1 k β i g i ( x ) \mathscr{L}(x,\beta) = f(x) + \sum_{i=1}^k\beta_ig_i(x) L(x,β)=f(x)+i=1∑kβigi(x)
所以我们可以假设以下情况:
1. 可行解满足 g ( x ) = 0 g(x)=0 g(x)=0,此时 β g ( x ) = 0 \beta g(x)=0 βg(x)=0,即 L ( x , β ) = f ( x ) \mathscr{L}(x,\beta) = f(x) L(x,β)=f(x),直接求解原函数的极小值。
2. 可行解满足 g ( x ) < 0 g(x)<0 g(x)<0,此时令 β = 0 \beta=0 β=0,因此 β g ( x ) = 0 \beta g(x) = 0 βg(x)=0,即 L ( x , β ) = f ( x ) \mathscr{L}(x,\beta) = f(x) L(x,β)=f(x),直接求解原函数的极小值。
因此现在的问题变成了 β \beta β 如何取得合适的值。在不等式优化中,如果 β = 0 \beta=0 β=0,此时的可行解是落在约束区域内的。而如果 β \beta\; β≠ 0 \;0 0,此时的可行解落在区域边界上,这时可行解应该要尽量靠近无约束时的解,因此在约束边界上,目标函数的负梯度方向应该与约束边界的梯度平行。
− ∂ f ( x ) ∂ x = β ∂ g ( x ) ∂ x -{\partial f(x)\over \partial x} = \beta{\partial g(x) \over \partial x} −∂x∂f(x)=β∂x∂g(x)
由此可见, β ≥ 0 \beta \geq 0 β≥0。且对于不等式约束,只要满足一定条件,也一样可以使用拉格朗日函数求解。这里的条件,就是 KKT条件。
KKT 条件
原始问题
假设存在 f ( x ) , h i ( x ) , g j ( x ) f(x),h_i(x),g_j(x) f(x),hi(x),gj(x) 是定义在 R n R^n Rn 上的连续可微函数,考虑约束优化问题:
min x ∈ R n f ( x ) s . t . h i ( x ) = 0 , i = 1 , 2 , 3 , … , m g j ( x ) ≤ 0 , j = 1 , 2 , 3 , … , k \min_{x\in R^n}f(x)\\ s.t.\ \ \ \ h_i(x) = 0,\ i=1,2,3,\dots,m\\ \ \ \ \ \ \ \ \ g_j(x)\leq0,\ j=1,2,3,\dots ,k x∈Rnminf(x)s.t. hi(x)=0, i=1,2,3,…,m gj(x)≤0, j=1,2,3,…,k
如果约束条件满足以下 KKT条件,也可以使用拉格朗日函数求解:
L ( x , α , β ) = f ( x ) + ∑ i = 1 m α i h i ( x ) + ∑ j = 1 k β j g j ( x ) \mathscr{L}(x, \alpha, \beta)=f(x)+\sum_{i=1}^m\alpha_ih_i(x) + \sum_{j=1}^k\beta_jg_j(x) L(x,α,β)=f(x)+i=1∑mαihi(x)+j=1∑kβjgj(x)
其中 KKT条件:
∂ L ( x , α , β ) ∂ x = 0 h i ( x ) = 0 , i = 1 , 2 , 3 , … , m g j ( x ) ≤ 0 , j = 1 , 2 , 3 , … , k β j g j ( x ) = 0 , j = 1 , 2 , 3 , … , k β j ≥ 0 , j = 1 , 2 , 3 , … , k \begin{aligned}\\ {\partial \mathscr{L}(x, \alpha, \beta)\over\partial x}&=0 \\ h_i(x)&=0,\ i =1,2,3,\dots,m\\ g_j(x)&\leq0,\ j=1,2,3,\dots,k\\ \beta_jg_j(x)&=0,\ j=1,2,3,\dots,k\\ \beta_j&\geq0,\ j=1,2,3,\dots,k\\ \end{aligned} ∂x∂L(x,α,β)hi(x)gj(x)βjgj(x)βj=0=0, i=1,2,3,…,m≤0, j=1,2,3,…,k=0, j=1,2,3,…,k≥0, j=1,2,3,…,k