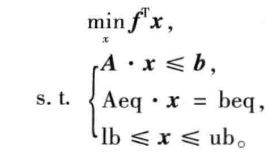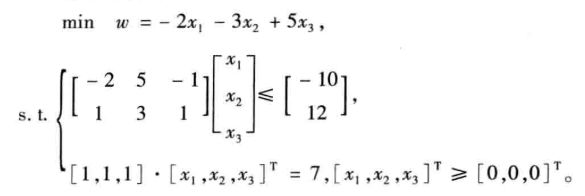第一章 线性规划

1.1线性规划问题（LP）

1.1.1 重要概念

决策变量：所需求问题的解
目标函数：所需求问题的表达式
约束条件（s.t.）：题给范围及实际情况
线性规划问题：目标函数和约束条件均为线性函数
（数学）标准型：
可行解：满足s.t.的解----->最优解
可行域：所有可行解的集合

1.1.2程序实现

matlab中标准形式：
例如：
化为标准形式为：

• 目标函数一定要是求最小值
• 约束条件不等号一定要是小于（等于）
• 等于需单独列出

程序如下：

f=[-2; -3; 5];%目标函数系数
a=[-2,5,-1;1,3,1];%不等号系数
b=[-10;12];%不等号结果
aeq=[1,1,1];%等号s.t.系数
beq=7;%等号s.t.结果
[x,y]=linprog(f,a,b,aeq,beq,zeros(3,1));
%调用函数，若没有等值约束则aeq,beq为[]
x, y=-y%结果y加负号，恢复原值

1.1.3转化问题

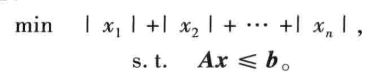
构造如下：
  对任意的x，存在非负数u，v满足:
  x = u - v，| x | = u + v
  令 u = (x + |x|) / 2，v = (|x| - x) / 2
转化为标准形式为:

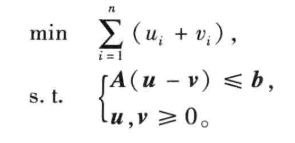
1.2多目标规划模型

目标函数：
模型简化：

1. 结合题意（多用于投资问题）给定界限，使其中一个函数化为约束条件，只保留其中一个
2. 结合题意，选择合适的权重，对目标函数进行组合

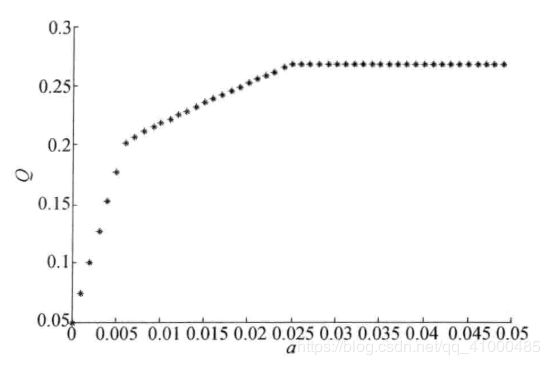
即把多目标规划问题变为单目标规划问题，在一定范围内，设置步长，进行枚举

书中以模型一的代码为例：

clc,clear
a=0;
hold on
while a<0.05
    c=[-0.05,-0.27,-0.19,-0.185,-0.185];
    A=[zeros(4,1),diag([0.025,0.015,0.055,0.026])];
    %第一列x0为0，对角化矩阵，其余为0
    b=a*ones(4,1);%4行1列的单位矩阵
    Aeq=[1,1.01,1.02,1.045,1.065];
    beq=1;
    LB=zeros(5,1);%对0的约束
    [x,Q]=linprog(c,A,b,Aeq,beq,LB);
    Q=-Q;%恢复原值
    plot(a,Q,'*k');
    a=a+0.001;%以0.001为步长
end
xlabel('a'),ylabel('Q')

结果如图：