双链表的基本操作

首先，双链表的结构声明如下：一个前驱节点的指针，一个后继节点的指针和数据域。

typedef struct node{
	int data;
	struct node	*prior;		//前驱节点 
	struct node *next;		//后继节点 
}Dlinklist;

1.头插法建表：与建立一个单链表的方法相似，从一个空表开始，向数据域读取数据，生成新的节点，将数据放到数据域内，然后将新节点插入到头结点之后，第一个数据节点之前，直到结束为止，与单链表的区别在于双链表还需要对前驱指针进行赋值。双链表的缺点与单链表一样，对输入的数据会反向输出。例程如下：

void creat_list(linklist *head)
{
	linklist p;
	int i;
	(*head) = (Dlinklist *)malloc(sizeof(Dlinklist));		//创建头结点
	(*head) -> next = (*head)-> prior = NULL; 
	for(i = 1;i < 11;i++)
	{
		p = (Dlinklist *)malloc(sizeof(Dlinklist));
		p -> data = i;
		p -> next = (*head) -> next;		//新节点插入到头结点之后，首节点之前
		if((*head) -> next)
			(*head) -> next -> prior = p;
		(*head) -> next = p;
		p -> prior = *head;
	}
}

2.尾插法建表：先给头结点申请内存来建立头结点，之后对新节点进行内存申请并进行新节点数据域的赋值，然后将头结点的指针域指向新节点，并将新节点交给头结点（头结点后移）最后将头结点指针域置空。尾插法的优势相对于 单链表来讲是一样的，尾插法的数据在进行输出的时候顺序与输入顺序相同。例程如下：

void creat_list(linklist *head)		//尾插法建表 
{
	linklist p,m;
	int i;
	(*head) = (linklist)malloc(sizeof(Dlinklist));
	m = (*head);		//头结点交给临时节点
	for(i = 1;i < 11;i++)
	{
		p = (linklist)malloc(sizeof(Dlinklist));		//新节点申请内存 
		p -> data = i;			//数据域赋值 
		m -> next = p;
		p -> prior = m;
		m = p;					//头结点后移 
	}
	m -> next = NULL;
}
//时间复杂度为O（n）

3.双链表查找指定元素值的节点：从第一个有数据的节点开始向后遍历双链表，若找到这样的节点就返回其序号。

int find(linklist head, int x)
{
	linklist L = head -> next;		//指向第一个有数据的节点 
	int i = 1;
	while(L && L -> data != x)
	{
		i++;			//计数器自增 
		L = L -> next;	//指针后继 
	}
	if(!L)
		puts("没有该节点,查找失败"); 
	else
		printf("数据为%d的节点在链表中的位置是第%d位\n", x, i);
}
//本算法时间复杂度为O（n）。

4.插入节点：在节点p之后插入节点s，过程图如下：

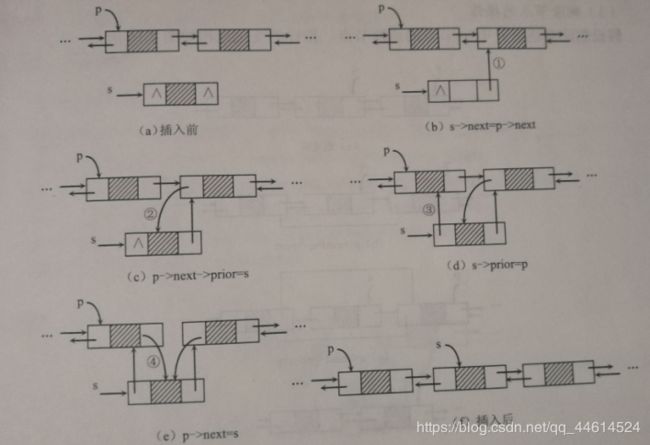
因为是在整个链表中插入数据，因此这里应该将头结点交给临时变量而不是将第一个有数据的节点交给临时节点，在单链表中如果想在某节点之前插入新节点需要我们找到该节点的前驱节点，而对于双链表，想在某一节点之前插入新节点，我们只要找到该节点即可。对应的具体算法如下：

void insert(Dlinklist **head, int i, int x)	//在i的位置插入数据x 
{
	int j = 0;
	linklist s, L = *head;			//注意赋值
	while(j < i - 1 && L)
	{
		j++;		//计数器进行计数来找位置
		L = L -> next;	//指针后继 
	}
	if(!L)
		puts("没有找到该位置");
	else				//如果找到了位置 
	{
		s = (Dlinklist *)malloc(sizeof(Dlinklist));
		s -> data = x;
		//新节点s插入到L之后（新结点后继指针指向插入位置之后的那个节点） 
		s -> next =  L -> next;		
		if(L -> next)				//若L存在后继节点 
			L -> next -> prior = s;		//将L的后继节点的前驱指向s
		s -> prior = L;
		L -> next = s;
		printf("在第%d个位置插入了%d之后的链表为\n", i, x); 
	}
}
//时间复杂度为O（n）。

5.删除节点：假设删除链表中某一节点的后继节点，指针的变化过程如图：
对应算法如下：

void delete(linklist *head, int i)
{
	Dlinklist *L = *head, *s;
	int j = 0;
	while(j < i - 1 && L)
	{
		j++;				//寻找正确的删除位置 
		L = L -> next;		//指针后继 
	}
	if(!L)					//如果没有找到该位置 
		puts("没有找到该位置，请重试");
	else
	{
		s = L -> next;  	//s指向要删除节点的后继节点
		if(!s)				//如果没有后继节点 
			puts("删除失败");	
		L -> next = s -> next;	//从链表中删除要删除的节点
		if(!L -> next)		//如果存在后继节点
		L -> next -> prior = L;  
		free(s);				//释放要删除的节点
		printf("删除第%d个位置的元素成功,删除之后的链表为\n", i); 
	} 
}
//时间复杂度为O（n）。