数据结构之树和二叉树算法实现（C语言）

待我学有所成，结发与蕊可好。@夏瑾墨

---

开发环境为Dev-C++ 5.11 编译器：MinGW GCC 6.1.0 64-bit
一、算法程序组建目录结构如下：
第一部分：头文件
1. c1.h
2. c3-3.h
3. c6-1.h
4. c6-2.h
5. c6-3.h
6. c6-4.h
7. c6-5.h
8. c6-7.h
第二部分：主程序入口文件
1.main6-1.c
2.main6-2.c
3.main6-3.c
4.main6-4.c
5.main6-5.c
6.main6-6.c
第三部分：核心程序
1.algo6-1.c
2.algo6-2.c
3.bo3-4.c
4.bo6-1.c
5.bo6-2.c
6.bo6-3.c
7.bo6-4.c
8.bo6-5.c
9.bo6-6.c
二、源码解析
https://github.com/Jooeys/DataStructures/tree/Binary-Tree

第一部分：头文件

 /* c1.h (程序名) */
 #include
 #include
 #include /* malloc()等 */
 #include /* INT_MAX等 */
 #include /* EOF(=^Z或F6),NULL */
 #include /* atoi() */
 #include /* eof() */
 #include /* floor(),ceil(),abs() */
 #include /* exit() */
 /* 函数结果状态代码 */
 #define TRUE 1
 #define FALSE 0
 #define OK 1
 #define ERROR 0
 #define INFEASIBLE -1
 /* #define OVERFLOW -2 因为在math.h中已定义OVERFLOW的值为3,故去掉此行 */
 typedef int Status; /* Status是函数的类型,其值是函数结果状态代码，如OK等 */
 typedef int Boolean; /* Boolean是布尔类型,其值是TRUE或FALSE */

 /* c3-3.h 队列的顺序存储结构(可用于循环队列和非循环队列) */
 #define MAXQSIZE 5 /* 最大队列长度(对于循环队列，最大队列长度要减1) */
 typedef struct
 {
   QElemType *base; /* 初始化的动态分配存储空间 */
   int front; /* 头指针,若队列不空,指向队列头元素 */
   int rear; /* 尾指针,若队列不空,指向队列尾元素的下一个位置 */
 }SqQueue;

 /* c6-1.h 二叉树的顺序存储表示 */
 #define MAX_TREE_SIZE 100 /* 二叉树的最大结点数 */
 typedef TElemType SqBiTree[MAX_TREE_SIZE]; /* 0号单元存储根结点 */

 typedef struct
 {
   int level,order; /* 结点的层,本层序号(按满二叉树计算) */
 }position;

 /* c6-2.h 二叉树的二叉链表存储表示 */
 typedef struct BiTNode
 {
   TElemType data;
   struct BiTNode *lchild,*rchild; /* 左右孩子指针 */
 }BiTNode,*BiTree;

 /* c6-3.h 二叉树的二叉线索存储表示 */
 typedef enum{Link,Thread}PointerTag; /* Link(0):指针,Thread(1):线索 */
 typedef struct BiThrNode
 {
   TElemType data;
   struct BiThrNode *lchild,*rchild; /* 左右孩子指针 */
   PointerTag LTag,RTag; /* 左右标志 */
 }BiThrNode,*BiThrTree;

 /* c6-4.h 树的双亲表存储表示 */
 #define MAX_TREE_SIZE 100
 typedef struct
 {
   TElemType data;
   int parent; /* 双亲位置域 */
 } PTNode;
 typedef struct
 {
   PTNode nodes[MAX_TREE_SIZE];
   int n; /* 结点数 */
 } PTree;

 /* c6-5.h 树的二叉链表(孩子－兄弟)存储表示 */
 typedef struct CSNode
 {
   TElemType data;
   struct CSNode *firstchild,*nextsibling;
 }CSNode,*CSTree;

 /* c6-5.h 树的二叉链表(孩子－兄弟)存储表示 */
 typedef struct CSNode
 {
   TElemType data;
   struct CSNode *firstchild,*nextsibling;
 }CSNode,*CSTree;

 /* c6-7.h 赫夫曼树和赫夫曼编码的存储表示 */
 typedef struct
 {
   unsigned int weight;
   unsigned int parent,lchild,rchild;
 }HTNode,*HuffmanTree; /* 动态分配数组存储赫夫曼树 */
 typedef char **HuffmanCode; /* 动态分配数组存储赫夫曼编码表 */

第二部分：主程序入口文件

 /* main6-1.c 检验bo6-1.c的主程序，利用<条件编译>选择数据类型为char或int */
 /*#define CHAR 1 /* 字符型 */
 #define CHAR 0 /* 整型(二者选一) */
 #include"c1.h"
 #if CHAR
   typedef char TElemType;
   TElemType Nil=' '; /* 设字符型以空格符为空 */
 #else
   typedef int TElemType;
   TElemType Nil=0; /* 设整型以0为空 */ 
 #endif
 #include"c6-1.h"
 #include"bo6-1.c"

 Status visit(TElemType e)
 {
   printf("%d ",e);
   return OK;
 }

 void main()
 {
   Status i;
   int j;
   position p;
   TElemType e;
   SqBiTree T,s;
   InitBiTree(T);
   CreateBiTree(T);
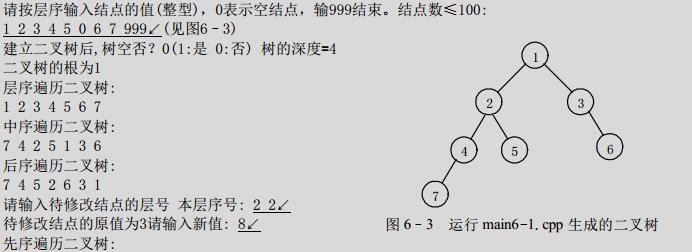
   printf("建立二叉树后,树空否？%d(1:是 0:否) 树的深度=%d\n",BiTreeEmpty(T),BiTreeDepth(T));
   i=Root(T,&e);
   if(i)
     printf("二叉树的根为：%d\n",e);
   else
     printf("树空，无根\n");
   printf("层序遍历二叉树:\n");
   LevelOrderTraverse(T,visit);
   printf("中序遍历二叉树:\n");
   InOrderTraverse(T,visit);
   printf("后序遍历二叉树:\n");
   PostOrderTraverse(T,visit);
   printf("请输入待修改结点的层号 本层序号: ");
   scanf("%d%d",&p.level,&p.order);
   e=Value(T,p);
   printf("待修改结点的原值为%d请输入新值: ",e);
   scanf("%d",&e);
   Assign(T,p,e);
   printf("先序遍历二叉树:\n");
   PreOrderTraverse(T,visit);
   printf("结点%d的双亲为%d,左右孩子分别为",e,Parent(T,e));
   printf("%d,%d,左右兄弟分别为",LeftChild(T,e),RightChild(T,e));
   printf("%d,%d\n",LeftSibling(T,e),RightSibling(T,e));
   InitBiTree(s);
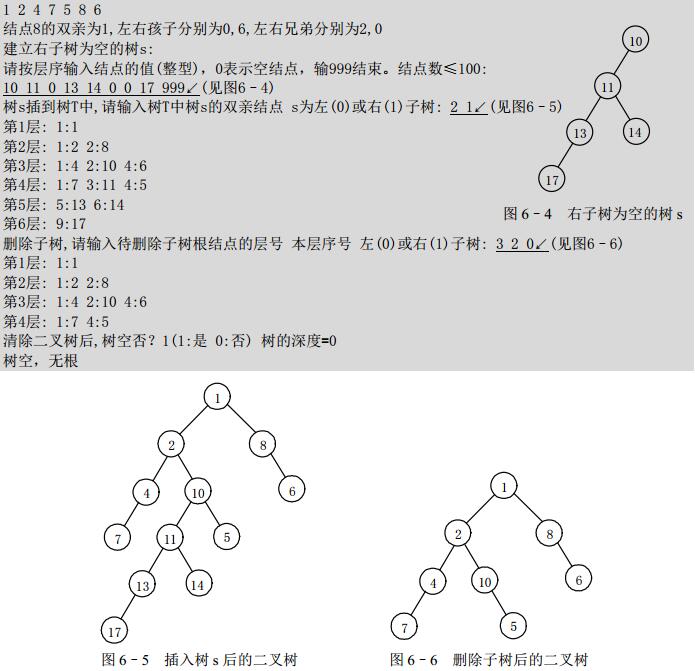
   printf("建立右子树为空的树s:\n");
   CreateBiTree(s);
   printf("树s插到树T中,请输入树T中树s的双亲结点 s为左(0)或右(1)子树: ");
   scanf("%d%d",&e,&j);
   InsertChild(T,e,j,s);
   Print(T);
   printf("删除子树,请输入待删除子树根结点的层号 本层序号 左(0)或右(1)子树: ");
   scanf("%d%d%d",&p.level,&p.order,&j);
   DeleteChild(T,p,j);
   Print(T);
   ClearBiTree(T);
   printf("清除二叉树后,树空否？%d(1:是 0:否) 树的深度=%d\n",BiTreeEmpty(T),BiTreeDepth(T));
   i=Root(T,&e);
   if(i)
     printf("二叉树的根为：%d\n",e);
   else
     printf("树空，无根\n");
 }

 /* main6-2.c 检验bo6-2.c的主程序,利用条件编译选择数据类型(另一种方法) */
 #define CHAR /* 字符型 */
 /* #define INT /* 整型（二者选一） */
 #include"c1.h"
 #ifdef CHAR
   typedef char TElemType;
   TElemType Nil=' '; /* 字符型以空格符为空 */
 #endif
 #ifdef INT
   typedef int TElemType;
   TElemType Nil=0; /* 整型以0为空 */
 #endif
 #include"c6-2.h"
 #include"bo6-2.c"

 Status visitT(TElemType e)
 {
 #ifdef CHAR
   printf("%c ",e);
 #endif
 #ifdef INT
   printf("%d ",e);
 #endif
   return OK;
 }

 void main()
 {
   int i;
   BiTree T,p,c;
   TElemType e1,e2;
   InitBiTree(&T);
   printf("构造空二叉树后,树空否？%d(1:是 0:否) 树的深度=%d\n",BiTreeEmpty(T),BiTreeDepth(T));
   e1=Root(T);
   if(e1!=Nil)
 #ifdef CHAR
     printf("二叉树的根为: %c\n",e1);
 #endif
 #ifdef INT
     printf("二叉树的根为: %d\n",e1);
 #endif
   else
     printf("树空，无根\n");
 #ifdef CHAR
   printf("请先序输入二叉树(如:ab三个空格表示a为根结点,b为左子树的二叉树)\n");
 #endif
 #ifdef INT
   printf("请先序输入二叉树(如:1 2 0 0 0表示1为根结点,2为左子树的二叉树)\n");
 #endif
   CreateBiTree(&T);
   printf("建立二叉树后,树空否？%d(1:是 0:否) 树的深度=%d\n",BiTreeEmpty(T),BiTreeDepth(T));
   e1=Root(T);
   if(e1!=Nil)
 #ifdef CHAR
     printf("二叉树的根为: %c\n",e1);
 #endif
 #ifdef INT
     printf("二叉树的根为: %d\n",e1);
 #endif
   else
     printf("树空，无根\n");
   printf("中序递归遍历二叉树:\n");
   InOrderTraverse(T,visitT);
   printf("\n中序非递归遍历二叉树:\n");
   InOrderTraverse1(T,visitT);
   printf("中序非递归遍历二叉树(另一种方法):\n");
   InOrderTraverse2(T,visitT);
   printf("后序递归遍历二叉树:\n");
   PostOrderTraverse(T,visitT);
   printf("\n层序遍历二叉树:\n");
   LevelOrderTraverse(T,visitT);
   printf("请输入一个结点的值: ");
 #ifdef CHAR
   scanf("%*c%c",&e1);
 #endif
 #ifdef INT
   scanf("%d",&e1);
 #endif
   p=Point(T,e1); /* p为e1的指针 */
 #ifdef CHAR
   printf("结点的值为%c\n",Value(p));
 #endif
 #ifdef INT
   printf("结点的值为%d\n",Value(p));
 #endif
   printf("欲改变此结点的值，请输入新值: ");
 #ifdef CHAR
   scanf("%*c%c%*c",&e2);
 #endif
 #ifdef INT
   scanf("%d",&e2);
 #endif
   Assign(p,e2);
   printf("层序遍历二叉树:\n");
   LevelOrderTraverse(T,visitT);
   e1=Parent(T,e2);
   if(e1!=Nil)
 #ifdef CHAR
     printf("%c的双亲是%c\n",e2,e1);
 #endif
 #ifdef INT
     printf("%d的双亲是%d\n",e2,e1);
 #endif
   else
 #ifdef CHAR
     printf("%c没有双亲\n",e2);
 #endif
 #ifdef INT
     printf("%d没有双亲\n",e2);
 #endif
   e1=LeftChild(T,e2);
   if(e1!=Nil)
 #ifdef CHAR
     printf("%c的左孩子是%c\n",e2,e1);
 #endif
 #ifdef INT
     printf("%d的左孩子是%d\n",e2,e1);
 #endif
   else
 #ifdef CHAR
     printf("%c没有左孩子\n",e2);
 #endif
 #ifdef INT
     printf("%d没有左孩子\n",e2);
 #endif
   e1=RightChild(T,e2);
   if(e1!=Nil)
 #ifdef CHAR
     printf("%c的右孩子是%c\n",e2,e1);
 #endif
 #ifdef INT
     printf("%d的右孩子是%d\n",e2,e1);
 #endif
   else
 #ifdef CHAR
     printf("%c没有右孩子\n",e2);
 #endif
 #ifdef INT
     printf("%d没有右孩子\n",e2);
 #endif
   e1=LeftSibling(T,e2);
   if(e1!=Nil)
 #ifdef CHAR
     printf("%c的左兄弟是%c\n",e2,e1);
 #endif
 #ifdef INT
     printf("%d的左兄弟是%d\n",e2,e1);
 #endif
   else
 #ifdef CHAR
     printf("%c没有左兄弟\n",e2);
 #endif
 #ifdef INT
     printf("%d没有左兄弟\n",e2);
 #endif
   e1=RightSibling(T,e2);
   if(e1!=Nil)
 #ifdef CHAR
     printf("%c的右兄弟是%c\n",e2,e1);
 #endif
 #ifdef INT
     printf("%d的右兄弟是%d\n",e2,e1);
 #endif
   else
 #ifdef CHAR
     printf("%c没有右兄弟\n",e2);
 #endif
 #ifdef INT
     printf("%d没有右兄弟\n",e2);
 #endif
   InitBiTree(&c);
   printf("构造一个右子树为空的二叉树c:\n");
 #ifdef CHAR
   printf("请先序输入二叉树(如:ab三个空格表示a为根结点,b为左子树的二叉树)\n");
 #endif
 #ifdef INT
   printf("请先序输入二叉树(如:1 2 0 0 0表示1为根结点,2为左子树的二叉树)\n");
 #endif
   CreateBiTree(&c);
   printf("先序递归遍历二叉树c:\n");
   PreOrderTraverse(c,visitT);
   printf("\n树c插到树T中,请输入树T中树c的双亲结点 c为左(0)或右(1)子树: ");
 #ifdef CHAR
   scanf("%*c%c%d",&e1,&i);
 #endif
 #ifdef INT
   scanf("%d%d",&e1,&i);
 #endif
   p=Point(T,e1); /* p是T中树c的双亲结点指针 */
   InsertChild(p,i,c);
   printf("先序递归遍历二叉树:\n");
   PreOrderTraverse(T,visitT);
   printf("\n删除子树,请输入待删除子树的双亲结点  左(0)或右(1)子树: ");
 #ifdef CHAR
   scanf("%*c%c%d",&e1,&i);
 #endif
 #ifdef INT
   scanf("%d%d",&e1,&i);
 #endif
   p=Point(T,e1);
   DeleteChild(p,i);
   printf("先序递归遍历二叉树:\n");
   PreOrderTraverse(T,visitT);
   printf("\n");
   DestroyBiTree(&T);
 }

 /* main6-3.c 检验bo6-3.c的主程序 */
 #define CHAR 1 /* 字符型 */
 /*#define CHAR 0 /* 整型(二者选一) */
 #if CHAR
   typedef char TElemType;
   TElemType Nil=' '; /* 字符型以空格符为空 */
 #else
   typedef int TElemType;
   TElemType Nil=0; /* 整型以0为空 */
 #endif
 #include"c1.h"
 #include"c6-3.h"
 #include"bo6-3.c"

 Status vi(TElemType c)
 {
 #if CHAR
   printf("%c ",c);
 #else
   printf("%d ",c);
 #endif
   return OK;
 }

 void main()
 {
   BiThrTree H,T;
 #if CHAR
   printf("请按先序输入二叉树(如:ab三个空格表示a为根结点,b为左子树的二叉树)\n");
 #else
   printf("请按先序输入二叉树(如:1 2 0 0 0表示1为根结点,2为左子树的二叉树)\n");
 #endif
   CreateBiThrTree(&T); /* 按先序产生二叉树 */
   InOrderThreading(&H,T); /* 中序遍历，并中序线索化二叉树 */
   printf("中序遍历(输出)二叉线索树:\n");
   InOrderTraverse_Thr(H,vi); /* 中序遍历(输出)二叉线索树 */
   printf("\n");
 }

  /* main6-4.c 检验bo6-4.c的主程序 */
 #include"c1.h"
 typedef char TElemType;
 TElemType Nil=' '; /* 以空格符为空 */
 #include"c6-4.h"
 #include"bo6-4.c"

 void vi(TElemType c)
 {
   printf("%c ",c);
 }

 void main()
 {
   int i;
   PTree T,p;
   TElemType e,e1;
   InitTree(&T);
   printf("构造空树后,树空否? %d(1:是 0:否) 树根为%c 树的深度为%d\n",TreeEmpty(T),Root(T),TreeDepth(T));
   CreateTree(&T);
   printf("构造树T后,树空否? %d(1:是 0:否) 树根为%c 树的深度为%d\n",TreeEmpty(T),Root(T),TreeDepth(T));
   printf("层序遍历树T:\n");
   TraverseTree(T,vi);
   printf("请输入待修改的结点的值 新值: ");
   scanf("%c%*c%c%*c",&e,&e1);
   Assign(&T,e,e1);
   printf("层序遍历修改后的树T:\n");
   TraverseTree(T,vi);
   printf("%c的双亲是%c,长子是%c,下一个兄弟是%c\n",e1,Parent(T,e1),LeftChild(T,e1),RightSibling(T,e1));
   printf("建立树p:\n");
   InitTree(&p);
   CreateTree(&p);
   printf("层序遍历树p:\n");
   TraverseTree(p,vi);
   printf("将树p插到树T中，请输入T中p的双亲结点 子树序号: ");
   scanf("%c%d%*c",&e,&i);
   InsertChild(&T,e,i,p);
   Print(T);
   printf("删除树T中结点e的第i棵子树，请输入e i: ");
   scanf("%c%d",&e,&i);
   DeleteChild(&T,e,i);
   Print(T);
 }

 /* main6-5.c 检验bo6-5.c的主程序 */
 #include"c1.h"
 typedef char TElemType;
 TElemType Nil=' '; /* 以空格符为空 */
 #include"c6-5.h"
 #include"bo6-5.c"

 void vi(TElemType c)
 {
   printf("%c ",c);
 }

 void main()
 {
   int i;
   CSTree T,p,q;
   TElemType e,e1;
   InitTree(&T);
   printf("构造空树后,树空否? %d(1:是 0:否) 树根为%c 树的深度为%d\n",TreeEmpty(T),Root(T),TreeDepth(T));
   CreateTree(&T);
   printf("构造树T后,树空否? %d(1:是 0:否) 树根为%c 树的深度为%d\n",TreeEmpty(T),Root(T),TreeDepth(T));
   printf("先根遍历树T:\n");
   PreOrderTraverse(T,vi);
   printf("\n请输入待修改的结点的值 新值: ");
   scanf("%c%*c%c%*c",&e,&e1);
   Assign(&T,e,e1);
   printf("后根遍历修改后的树T:\n");
   PostOrderTraverse(T,vi);
   printf("\n%c的双亲是%c,长子是%c,下一个兄弟是%c\n",e1,Parent(T,e1),LeftChild(T,e1),RightSibling(T,e1));
   printf("建立树p:\n");
   InitTree(&p);
   CreateTree(&p);
   printf("层序遍历树p:\n");
   LevelOrderTraverse(p,vi);
   printf("\n将树p插到树T中，请输入T中p的双亲结点 子树序号: ");
   scanf("%c%d%*c",&e,&i);
   q=Point(T,e);
   InsertChild(&T,q,i,p);
   printf("层序遍历树T:\n");
   LevelOrderTraverse(T,vi);
   printf("\n删除树T中结点e的第i棵子树，请输入e i: ");
   scanf("%c%d",&e,&i);
   q=Point(T,e);
   DeleteChild(&T,q,i);
   printf("层序遍历树T:\n",e,i);
   LevelOrderTraverse(T,vi);
   printf("\n");
   DestroyTree(&T);
 }

 /* main6-6.c 检验bo6-6.c的主程序 */
 #define CHAR /* 字符型 */
 /*#define INT /* 整型（二者选一） */
 #include"c1.h"
 #ifdef CHAR
   typedef char TElemType;
   TElemType Nil=' '; /* 字符型以空格符为空 */
 #endif
 #ifdef INT
   typedef int TElemType;
   TElemType Nil=0; /* 整型以0为空 */
 #endif
 #include"c6-6.h"
 #include"bo6-6.c"

 Status visitT(BiPTree T)
 {
   if(T) /* T非空 */
 #ifdef CHAR
     printf("%c是",T->data);
   if(T->parent) /* T有双亲 */
   {
     printf("%c",T->parent->data);
 #endif
 #ifdef INT
     printf("%d是",T->data);
   if(T->parent) /* T有双亲 */
   {
     printf("%d",T->parent->data);
 #endif
     if(T->parent->lchild==T)
       printf("的左孩子\n");
     else
       printf("的右孩子\n");
   }
   else
     printf("根结点\n");
   return OK;
 }

 void main()
 {
   int i;
   BiPTree T,c,q;
   TElemType e1,e2;
   InitBiTree(&T);
   printf("构造空二叉树后,树空否？%d(1:是 0:否) 树的深度=%d\n",BiTreeEmpty(T),BiTreeDepth(T));
   e1=Root(T);
   if(e1!=Nil)
 #ifdef CHAR
     printf("二叉树的根为: %c\n",e1);
 #endif
 #ifdef INT
     printf("二叉树的根为: %d\n",e1);
 #endif
   else
     printf("树空，无根\n");
 #ifdef CHAR
   printf("请按先序输入二叉树(如:ab三个空格表示a为根结点,b为左子树的二叉树)\n");
 #endif
 #ifdef INT
   printf("请按先序输入二叉树(如:1 2 0 0 0表示1为根结点,2为左子树的二叉树)\n");
 #endif
   CreateBiTree(&T);
   printf("建立二叉树后,树空否？%d(1:是 0:否) 树的深度=%d\n",BiTreeEmpty(T),BiTreeDepth(T));
   e1=Root(T);
   if(e1!=Nil)
 #ifdef CHAR
     printf("二叉树的根为: %c\n",e1);
 #endif
 #ifdef INT
     printf("二叉树的根为: %d\n",e1);
 #endif
   else
     printf("树空，无根\n");
   printf("中序递归遍历二叉树:\n");
   InOrderTraverse(T,visitT);
   printf("后序递归遍历二叉树:\n");
   PostOrderTraverse(T,visitT);
   scanf("%*c"); /* 吃掉回车符 */
   printf("按回车键继续:");
   getchar(); /* 暂停输出 */
   printf("层序遍历二叉树:\n");
   LevelOrderTraverse(T,visitT);
   printf("请输入一个结点的值: ");
 #ifdef CHAR
   scanf("%c",&e1);
 #endif
 #ifdef INT
   scanf("%d",&e1);
 #endif
   c=Point(T,e1); /* c为e1的指针 */
 #ifdef CHAR
   printf("结点的值为%c\n",Value(c));
 #endif
 #ifdef INT
   printf("结点的值为%d\n",Value(c));
 #endif
   printf("欲改变此结点的值，请输入新值: ");
 #ifdef CHAR
   scanf("%*c%c%*c",&e2);
 #endif
 #ifdef INT
   scanf("%d",&e2);
 #endif
   Assign(c,e2);
   printf("层序遍历二叉树:\n");
   LevelOrderTraverse(T,visitT);
   e1=Parent(T,e2);
   if(e1!=Nil)
 #ifdef CHAR
     printf("%c的双亲是%c\n",e2,e1);
 #endif
 #ifdef INT
     printf("%d的双亲是%d\n",e2,e1);
 #endif
   else
 #ifdef CHAR
     printf("%c没有双亲\n",e2);
 #endif
 #ifdef INT
     printf("%d没有双亲\n",e2);
 #endif
   e1=LeftChild(T,e2);
   if(e1!=Nil)
 #ifdef CHAR
     printf("%c的左孩子是%c\n",e2,e1);
 #endif
 #ifdef INT
     printf("%d的左孩子是%d\n",e2,e1);
 #endif
   else
 #ifdef CHAR
     printf("%c没有左孩子\n",e2);
 #endif
 #ifdef INT
     printf("%d没有左孩子\n",e2);
 #endif
   e1=RightChild(T,e2);
   if(e1!=Nil)
 #ifdef CHAR
     printf("%c的右孩子是%c\n",e2,e1);
 #endif
 #ifdef INT
     printf("%d的右孩子是%d\n",e2,e1);
 #endif
   else
 #ifdef CHAR
     printf("%c没有右孩子\n",e2);
 #endif
 #ifdef INT
     printf("%d没有右孩子\n",e2);
 #endif
   e1=LeftSibling(T,e2);
   if(e1!=Nil)
 #ifdef CHAR
     printf("%c的左兄弟是%c\n",e2,e1);
 #endif
 #ifdef INT
     printf("%d的左兄弟是%d\n",e2,e1);
 #endif
   else
 #ifdef CHAR
     printf("%c没有左兄弟\n",e2);
 #endif
 #ifdef INT
     printf("%d没有左兄弟\n",e2);
 #endif
   e1=RightSibling(T,e2);
   if(e1!=Nil)
 #ifdef CHAR
     printf("%c的右兄弟是%c\n",e2,e1);
 #endif
 #ifdef INT
     printf("%d的右兄弟是%d\n",e2,e1);
 #endif
   else
 #ifdef CHAR
     printf("%c没有右兄弟\n",e2);
 #endif
 #ifdef INT
     printf("%d没有右兄弟\n",e2);
 #endif 
   InitBiTree(&c);
   printf("构造一个右子树为空的二叉树c:\n");
 #ifdef CHAR
   printf("请先序输入二叉树(如:ab三个空格表示a为根结点,b为左子树的二叉树)\n");
 #endif
 #ifdef INT
   printf("请先序输入二叉树(如:1 2 0 0 0表示1为根结点,2为左子树的二叉树)\n");
 #endif
   CreateBiTree(&c);
   printf("先序递归遍历二叉树c:\n");
   PreOrderTraverse(c,visitT);
   printf("树c插到树T中,请输入树T中树c的双亲结点 c为左(0)或右(1)子树: ");
 #ifdef CHAR
   scanf("%*c%c%d",&e1,&i);
 #endif
 #ifdef INT
   scanf("%d%d",&e1,&i);
 #endif
   q=Point(T,e1);
   InsertChild(q,i,c);
   printf("先序递归遍历二叉树:\n");
   PreOrderTraverse(T,visitT);
   printf("删除子树,请输入待删除子树的双亲结点  左(0)或右(1)子树: ");
 #ifdef CHAR
   scanf("%*c%c%d",&e1,&i);
 #endif
 #ifdef INT
   scanf("%d%d",&e1,&i);
 #endif
   q=Point(T,e1);
   DeleteChild(q,i);
   printf("先序递归遍历二叉树:\n");
   PreOrderTraverse(T,visitT);
   DestroyBiTree(&T);
 }

第三部分：核心程序组件

 /* algo6-1.c 求赫夫曼编码。实现算法6.12的程序 */
 #include"c1.h"
 #include"c6-7.h"

 int min1(HuffmanTree t,int i)
 { /* 函数void select()调用 */
   int j,flag;
   unsigned int k=UINT_MAX; /* 取k为不小于可能的值 */
   for(j=1;j<=i;j++)
     if(t[j].weight0)
       k=t[j].weight,flag=j;
   t[flag].parent=1;
   return flag;
 }

 void select(HuffmanTree t,int i,int *s1,int *s2)
 { /* s1为最小的两个值中序号小的那个 */
   int j;
   *s1=min1(t,i);
   *s2=min1(t,i);
   if(*s1>*s2)
   {
     j=*s1;
     *s1=*s2;
     *s2=j;
   }
 }

 void HuffmanCoding(HuffmanTree *HT,HuffmanCode *HC,int *w,int n) /* 算法6.12 */
 { /* w存放n个字符的权值(均>0),构造赫夫曼树HT,并求出n个字符的赫夫曼编码HC */
   int m,i,s1,s2,start;
   unsigned c,f;
   HuffmanTree p;
   char *cd;
   if(n<=1)
     return;
   m=2*n-1;
   *HT=(HuffmanTree)malloc((m+1)*sizeof(HTNode)); /* 0号单元未用 */
   for(p=*HT+1,i=1;i<=n;++i,++p,++w)
   {
     (*p).weight=*w;
     (*p).parent=0;
     (*p).lchild=0;
     (*p).rchild=0;
   }
   for(;i<=m;++i,++p)
     (*p).parent=0;
   for(i=n+1;i<=m;++i) /* 建赫夫曼树 */
   { /* 在HT[1~i-1]中选择parent为0且weight最小的两个结点,其序号分别为s1和s2 */
     select(*HT,i-1,&s1,&s2);
     (*HT)[s1].parent=(*HT)[s2].parent=i;
     (*HT)[i].lchild=s1;
     (*HT)[i].rchild=s2;
     (*HT)[i].weight=(*HT)[s1].weight+(*HT)[s2].weight;
   }
   /* 从叶子到根逆向求每个字符的赫夫曼编码 */
   *HC=(HuffmanCode)malloc((n+1)*sizeof(char*));
   /* 分配n个字符编码的头指针向量([0]不用) */
   cd=(char*)malloc(n*sizeof(char)); /* 分配求编码的工作空间 */
   cd[n-1]='\0'; /* 编码结束符 */
   for(i=1;i<=n;i++)
   { /* 逐个字符求赫夫曼编码 */
     start=n-1; /* 编码结束符位置 */
     for(c=i,f=(*HT)[i].parent;f!=0;c=f,f=(*HT)[f].parent)
     /* 从叶子到根逆向求编码 */
       if((*HT)[f].lchild==c)
         cd[--start]='0';
       else
         cd[--start]='1';
     (*HC)[i]=(char*)malloc((n-start)*sizeof(char));
     /* 为第i个字符编码分配空间 */
     strcpy((*HC)[i],&cd[start]); /* 从cd复制编码(串)到HC */
   }
   free(cd); /* 释放工作空间 */
 }

 void main()
 {
   HuffmanTree HT;
   HuffmanCode HC;
   int *w,n,i;
   printf("请输入权值的个数(>1)：");
   scanf("%d",&n);
   w=(int*)malloc(n*sizeof(int));
   printf("请依次输入%d个权值(整型)：\n",n);
   for(i=0;i<=n-1;i++)
     scanf("%d",w+i);
   HuffmanCoding(&HT,&HC,w,n);
   for(i=1;i<=n;i++)
     puts(HC[i]);
 }

 /* algo6-2.cpp 实现算法6.13的程序，前半部分与algo6-1.cpp同 */
 #include"c1.h"
 #include"c6-7.h"

 int min1(HuffmanTree t,int i)
 { /* 函数void select()调用 */
   int j,flag;
   unsigned int k=UINT_MAX; /* 取k为不小于可能的值 */
   for(j=1;j<=i;j++)
     if(t[j].weight0)
       k=t[j].weight,flag=j;
   t[flag].parent=1;
   return flag;
 }

 void select(HuffmanTree t,int i,int *s1,int *s2)
 { /* s1为最小的两个值中序号小的那个 */
   int j;
   *s1=min1(t,i);
   *s2=min1(t,i);
   if(*s1>*s2)
   {
     j=*s1;
     *s1=*s2;
     *s2=j;
   }
 } /* 以上同algo6-1.c */

 void HuffmanCoding(HuffmanTree *HT,HuffmanCode *HC,int *w,int n) /* 前半部分为算法6.12 */
 { /* w存放n个字符的权值(均>0),构造赫夫曼树HT,并求出n个字符的赫夫曼编码HC */
   int m,i,s1,s2; /* 此句与algo6-1.c不同 */
   unsigned c,cdlen; /* 此句与algo6-1.c不同 */
   HuffmanTree p;
   char *cd;
   if(n<=1)
     return;
   m=2*n-1;
   *HT=(HuffmanTree)malloc((m+1)*sizeof(HTNode)); /* 0号单元未用 */
   for(p=*HT+1,i=1;i<=n;++i,++p,++w)
   {
     (*p).weight=*w;
     (*p).parent=0;
     (*p).lchild=0;
     (*p).rchild=0;
   }
   for(;i<=m;++i,++p)
     (*p).parent=0;
   for(i=n+1;i<=m;++i) /* 建赫夫曼树 */
   { /* 在HT[1~i-1]中选择parent为0且weight最小的两个结点,其序号分别为s1和s2 */
     select(*HT,i-1,&s1,&s2);
     (*HT)[s1].parent=(*HT)[s2].parent=i;
     (*HT)[i].lchild=s1;
     (*HT)[i].rchild=s2;
     (*HT)[i].weight=(*HT)[s1].weight+(*HT)[s2].weight;
   }
   /* 以下为算法6.13，无栈非递归遍历赫夫曼树,求赫夫曼编码，以上同算法6.12 */
   *HC=(HuffmanCode)malloc((n+1)*sizeof(char*));
   /* 分配n个字符编码的头指针向量([0]不用) */
   cd=(char*)malloc(n*sizeof(char)); /* 分配求编码的工作空间 */
   c=m;
   cdlen=0;
   for(i=1;i<=m;++i)
     (*HT)[i].weight=0; /* 遍历赫夫曼树时用作结点状态标志 */
   while(c)
   {
     if((*HT)[c].weight==0)
     { /* 向左 */
       (*HT)[c].weight=1;
       if((*HT)[c].lchild!=0)
       {
         c=(*HT)[c].lchild;
         cd[cdlen++]='0';
       }
       else if((*HT)[c].rchild==0)
       { /* 登记叶子结点的字符的编码 */
         (*HC)[c]=(char *)malloc((cdlen+1)*sizeof(char));
         cd[cdlen]='\0';
         strcpy((*HC)[c],cd); /* 复制编码(串) */
       }
     }
     else if((*HT)[c].weight==1)
     { /* 向右 */
       (*HT)[c].weight=2;
       if((*HT)[c].rchild!=0)
       {
         c=(*HT)[c].rchild;
         cd[cdlen++]='1';
       }
     }
     else
     { /* HT[c].weight==2,退回 */
       (*HT)[c].weight=0;
       c=(*HT)[c].parent;
       --cdlen; /* 退到父结点,编码长度减1 */
     }
   }
   free(cd);
 }

 void main()
 { /* 主程序同algo6-1.c */
   HuffmanTree HT;
   HuffmanCode HC;
   int *w,n,i;
   printf("请输入权值的个数(>1)：");
   scanf("%d",&n);
   w=(int *)malloc(n*sizeof(int));
   printf("请依次输入%d个权值(整型)：\n",n);
   for(i=0;i<=n-1;i++)
     scanf("%d",w+i);
   HuffmanCoding(&HT,&HC,w,n);
   for(i=1;i<=n;i++)
     puts(HC[i]);
 }

 /* bo3-4.c 顺序队列(非循环,存储结构由c3-3.h定义)的基本操作(9个) */
 Status InitQueue(SqQueue *Q)
 { /* 构造一个空队列Q */
   (*Q).base=(QElemType *)malloc(MAXQSIZE*sizeof(QElemType));
   if(!(*Q).base) /* 存储分配失败 */
     exit(OVERFLOW);
   (*Q).front=(*Q).rear=0;
   return OK;
 }

 Status DestroyQueue(SqQueue *Q)
 { /* 销毁队列Q,Q不再存在 */
   if((*Q).base)
     free((*Q).base);
   (*Q).base=NULL;
   (*Q).front=(*Q).rear=0;
   return OK;
 }

 Status ClearQueue(SqQueue *Q)
 { /* 将Q清为空队列 */
   (*Q).front=(*Q).rear=0;
   return OK;
 }

 Status QueueEmpty(SqQueue Q)
 { /* 若队列Q为空队列,则返回TRUE,否则返回FALSE */
   if(Q.front==Q.rear) /* 队列空的标志 */
     return TRUE;
   else
     return FALSE;
 }

 int QueueLength(SqQueue Q)
 { /* 返回Q的元素个数,即队列的长度 */
   return(Q.rear-Q.front);
 }

 Status GetHead(SqQueue Q,QElemType *e)
 { /* 若队列不空,则用e返回Q的队头元素,并返回OK,否则返回ERROR */
   if(Q.front==Q.rear) /* 队列空 */
     return ERROR;
   *e=*(Q.base+Q.front);
   return OK;
 }

 Status EnQueue(SqQueue *Q,QElemType e)
 { /* 插入元素e为Q的新的队尾元素 */
   if((*Q).rear>=MAXQSIZE)
   { /* 队列满，增加1个存储单元 */
     (*Q).base=(QElemType *)realloc((*Q).base,((*Q).rear+1)*sizeof(QElemType));
     if(!(*Q).base) /* 增加单元失败 */
       return ERROR;
   }
   *((*Q).base+(*Q).rear)=e;
   (*Q).rear++;
   return OK;
 }

 Status DeQueue(SqQueue *Q,QElemType *e)
 { /* 若队列不空,则删除Q的队头元素,用e返回其值,并返回OK,否则返回ERROR */
   if((*Q).front==(*Q).rear) /* 队列空 */
     return ERROR;
   *e=(*Q).base[(*Q).front];
   (*Q).front=(*Q).front+1;
   return OK;
 }

 Status QueueTraverse(SqQueue Q,void(*vi)(QElemType))
 { /* 从队头到队尾依次对队列Q中每个元素调用函数vi()。一旦vi失败,则操作失败 */
   int i;
   i=Q.front;
   while(i!=Q.rear)
   {
     vi(*(Q.base+i));
     i++;
   }
   printf("\n");
   return OK;
 }

 /* bo6-1.c 二叉树的顺序存储(存储结构由c6-1.h定义)的基本操作(23个) */
 Status InitBiTree(SqBiTree T)
 { /* 构造空二叉树T。因为T是固定数组，不会改变，故不需要& */
   int i;
   for(i=0;i/* 初值为空 */
   return OK;
 }

 void DestroyBiTree()
 { /* 由于SqBiTree是定长类型,无法销毁 */
 }

 Status CreateBiTree(SqBiTree T)
 { /* 按层序次序输入二叉树中结点的值(字符型或整型), 构造顺序存储的二叉树T */
   int i=0;
 #if CHAR
   int l;
   char s[MAX_TREE_SIZE];
   printf("请按层序输入结点的值(字符)，空格表示空结点，结点数≤%d:\n",MAX_TREE_SIZE);
   gets(s); /* 输入字符串 */
   l=strlen(s); /* 求字符串的长度 */
   for(;i/* 将字符串赋值给T */
   {
     T[i]=s[i];
     if(i!=0&&T[(i+1)/2-1]==Nil&&T[i]!=Nil) /* 此结点(不空)无双亲且不是根 */
     {
       printf("出现无双亲的非根结点%c\n",T[i]);
       exit(ERROR);
     }
   }
   for(i=l;i/* 将空赋值给T的后面的结点 */
     T[i]=Nil;
 #else
   printf("请按层序输入结点的值(整型)，0表示空结点，输999结束。结点数≤%d:\n",MAX_TREE_SIZE);
   while(1)
   {
     scanf("%d",&T[i]);
     if(T[i]==999)
       break;
     if(i!=0&&T[(i+1)/2-1]==Nil&&T[i]!=Nil) /* 此结点(不空)无双亲且不是根 */
     {
       printf("出现无双亲的非根结点%d\n",T[i]);
       exit(ERROR);
     }
     i++;
   }
   while(i/* 将空赋值给T的后面的结点 */
     i++;
   }
 #endif
   return OK;
 }

 #define ClearBiTree InitBiTree /* 在顺序存储结构中，两函数完全一样 */

 Status BiTreeEmpty(SqBiTree T)
 { /* 初始条件: 二叉树T存在 */
   /* 操作结果: 若T为空二叉树,则返回TRUE,否则FALSE */
   if(T[0]==Nil) /* 根结点为空,则树空 */
     return TRUE;
   else
     return FALSE;
 }

 int BiTreeDepth(SqBiTree T)
 { /* 初始条件: 二叉树T存在。操作结果: 返回T的深度 */
   int i,j=-1;
   for(i=MAX_TREE_SIZE-1;i>=0;i--) /* 找到最后一个结点 */
     if(T[i]!=Nil)
       break;
   i++; /* 为了便于计算 */
   do
     j++;
   while(i>=pow(2,j));
   return j;
 }

 Status Root(SqBiTree T,TElemType *e)
 { /* 初始条件: 二叉树T存在 */
   /* 操作结果:  当T不空,用e返回T的根,返回OK;否则返回ERROR,e无定义 */
   if(BiTreeEmpty(T)) /* T空 */
     return ERROR;
   else
   {
     *e=T[0];
     return OK;
   }
 }

 TElemType Value(SqBiTree T,position e)
 { /* 初始条件: 二叉树T存在,e是T中某个结点(的位置) */
   /* 操作结果: 返回处于位置e(层,本层序号)的结点的值 */
   return T[(int)pow(2,e.level-1)+e.order-2];
 }

 Status Assign(SqBiTree T,position e,TElemType value)
 { /* 初始条件: 二叉树T存在,e是T中某个结点(的位置) */
   /* 操作结果: 给处于位置e(层,本层序号)的结点赋新值value */
   int i=(int)pow(2,e.level-1)+e.order-2; /* 将层、本层序号转为矩阵的序号 */
   if(value!=Nil&&T[(i+1)/2-1]==Nil) /* 给叶子赋非空值但双亲为空 */
     return ERROR;
   else if(value==Nil&&(T[i*2+1]!=Nil||T[i*2+2]!=Nil)) /*  给双亲赋空值但有叶子（不空） */
     return ERROR;
   T[i]=value;
   return OK;
 }

 TElemType Parent(SqBiTree T,TElemType e)
 { /* 初始条件: 二叉树T存在,e是T中某个结点 */
   /* 操作结果: 若e是T的非根结点,则返回它的双亲,否则返回＂空＂ */
   int i;
   if(T[0]==Nil) /* 空树 */
     return Nil;
   for(i=1;i<=MAX_TREE_SIZE-1;i++)
     if(T[i]==e) /* 找到e */
       return T[(i+1)/2-1];
   return Nil; /* 没找到e */
 }

 TElemType LeftChild(SqBiTree T,TElemType e)
 { /* 初始条件: 二叉树T存在,e是T中某个结点 */
   /* 操作结果: 返回e的左孩子。若e无左孩子,则返回＂空＂ */
   int i;
   if(T[0]==Nil) /* 空树 */
     return Nil;
   for(i=0;i<=MAX_TREE_SIZE-1;i++)
     if(T[i]==e) /* 找到e */
       return T[i*2+1];
   return Nil; /* 没找到e */
 }

 TElemType RightChild(SqBiTree T,TElemType e)
 { /* 初始条件: 二叉树T存在,e是T中某个结点 */
   /* 操作结果: 返回e的右孩子。若e无右孩子,则返回＂空＂ */
   int i;
   if(T[0]==Nil) /* 空树 */
     return Nil;
   for(i=0;i<=MAX_TREE_SIZE-1;i++)
     if(T[i]==e) /* 找到e */
       return T[i*2+2];
   return Nil; /* 没找到e */
 }

 TElemType LeftSibling(SqBiTree T,TElemType e)
 { /* 初始条件: 二叉树T存在,e是T中某个结点 */
   /* 操作结果: 返回e的左兄弟。若e是T的左孩子或无左兄弟,则返回＂空＂ */
   int i;
   if(T[0]==Nil) /* 空树 */
     return Nil;
   for(i=1;i<=MAX_TREE_SIZE-1;i++)
     if(T[i]==e&&i%2==0) /* 找到e且其序号为偶数(是右孩子) */
       return T[i-1];
   return Nil; /* 没找到e */
 }

 TElemType RightSibling(SqBiTree T,TElemType e)
 { /* 初始条件: 二叉树T存在,e是T中某个结点 */
   /* 操作结果: 返回e的右兄弟。若e是T的右孩子或无右兄弟,则返回＂空＂ */
   int i;
   if(T[0]==Nil) /* 空树 */
     return Nil;
   for(i=1;i<=MAX_TREE_SIZE-1;i++)
     if(T[i]==e&&i%2) /* 找到e且其序号为奇数(是左孩子) */
       return T[i+1];
   return Nil; /* 没找到e */
 }

 void Move(SqBiTree q,int j,SqBiTree T,int i) /* InsertChild()用到。加 */
 { /* 把从q的j结点开始的子树移为从T的i结点开始的子树 */
   if(q[2*j+1]!=Nil) /* q的左子树不空 */
     Move(q,(2*j+1),T,(2*i+1)); /* 把q的j结点的左子树移为T的i结点的左子树 */
   if(q[2*j+2]!=Nil) /* q的右子树不空 */
     Move(q,(2*j+2),T,(2*i+2)); /* 把q的j结点的右子树移为T的i结点的右子树 */
   T[i]=q[j]; /* 把q的j结点移为T的i结点 */
   q[j]=Nil; /* 把q的j结点置空 */
 }

 Status InsertChild(SqBiTree T,TElemType p,Status LR,SqBiTree c)
 { /* 初始条件: 二叉树T存在,p是T中某个结点的值,LR为0或1,非空二叉树c与T */
   /*           不相交且右子树为空 */
   /* 操作结果: 根据LR为0或1,插入c为T中p结点的左或右子树。p结点的原有左或 */
   /*           右子树则成为c的右子树 */
   int j,k,i=0;
   for(j=0;j<(int)pow(2,BiTreeDepth(T))-1;j++) /* 查找p的序号 */
     if(T[j]==p) /* j为p的序号 */
       break;
   k=2*j+1+LR; /* k为p的左或右孩子的序号 */
   if(T[k]!=Nil) /* p原来的左或右孩子不空 */
     Move(T,k,T,2*k+2); /* 把从T的k结点开始的子树移为从k结点的右子树开始的子树 */
   Move(c,i,T,k); /* 把从c的i结点开始的子树移为从T的k结点开始的子树 */
   return OK;
 }

 typedef int QElemType; /* 设队列元素类型为整型(序号) */
 #include "c3-3.h" /* 顺序非循环队列 */
 #include "bo3-4.c" /* 顺序非循环队列的基本操作 */
 Status DeleteChild(SqBiTree T,position p,int LR)
 { /* 初始条件: 二叉树T存在,p指向T中某个结点,LR为1或0 */
   /* 操作结果: 根据LR为1或0,删除T中p所指结点的左或右子树 */
   int i;
   Status k=OK; /* 队列不空的标志 */
   SqQueue q;
   InitQueue(&q); /* 初始化队列，用于存放待删除的结点 */
   i=(int)pow(2,p.level-1)+p.order-2; /* 将层、本层序号转为矩阵的序号 */
   if(T[i]==Nil) /* 此结点空 */
     return ERROR;
   i=i*2+1+LR; /* 待删除子树的根结点在矩阵中的序号 */
   while(k)
   {
     if(T[2*i+1]!=Nil) /* 左结点不空 */
       EnQueue(&q,2*i+1); /* 入队左结点的序号 */
     if(T[2*i+2]!=Nil) /* 右结点不空 */
       EnQueue(&q,2*i+2); /* 入队右结点的序号 */
     T[i]=Nil; /* 删除此结点 */
     k=DeQueue(&q,&i); /* 队列不空 */
   }
   return OK;
 }

 Status(*VisitFunc)(TElemType); /* 函数变量 */
 void PreTraverse(SqBiTree T,int e)
 { /* PreOrderTraverse()调用 */
   VisitFunc(T[e]);
   if(T[2*e+1]!=Nil) /* 左子树不空 */
     PreTraverse(T,2*e+1);
   if(T[2*e+2]!=Nil) /* 右子树不空 */
     PreTraverse(T,2*e+2);
 }

 Status PreOrderTraverse(SqBiTree T,Status(*Visit)(TElemType))
 { /* 初始条件: 二叉树存在,Visit是对结点操作的应用函数 */
   /* 操作结果: 先序遍历T,对每个结点调用函数Visit一次且仅一次。 */
   /*           一旦Visit()失败,则操作失败 */
   VisitFunc=Visit;
   if(!BiTreeEmpty(T)) /* 树不空 */
     PreTraverse(T,0);
   printf("\n");
   return OK;
 }

 void InTraverse(SqBiTree T,int e)
 { /* InOrderTraverse()调用 */
   if(T[2*e+1]!=Nil) /* 左子树不空 */
     InTraverse(T,2*e+1);
   VisitFunc(T[e]);
   if(T[2*e+2]!=Nil) /* 右子树不空 */
     InTraverse(T,2*e+2);
 }

 Status InOrderTraverse(SqBiTree T,Status(*Visit)(TElemType))
 { /* 初始条件: 二叉树存在,Visit是对结点操作的应用函数 */
   /* 操作结果: 中序遍历T,对每个结点调用函数Visit一次且仅一次。 */
   /*           一旦Visit()失败,则操作失败 */
   VisitFunc=Visit;
   if(!BiTreeEmpty(T)) /* 树不空 */
     InTraverse(T,0);
   printf("\n");
   return OK;
 }

 void PostTraverse(SqBiTree T,int e)
 { /* PostOrderTraverse()调用 */
   if(T[2*e+1]!=Nil) /* 左子树不空 */
     PostTraverse(T,2*e+1);
   if(T[2*e+2]!=Nil) /* 右子树不空 */
     PostTraverse(T,2*e+2);
   VisitFunc(T[e]);
 }

 Status PostOrderTraverse(SqBiTree T,Status(*Visit)(TElemType))
 { /* 初始条件: 二叉树T存在,Visit是对结点操作的应用函数 */
   /* 操作结果: 后序遍历T,对每个结点调用函数Visit一次且仅一次。 */
   /*           一旦Visit()失败,则操作失败 */
   VisitFunc=Visit;
   if(!BiTreeEmpty(T)) /* 树不空 */
     PostTraverse(T,0);
   printf("\n");
   return OK;
 }

 void LevelOrderTraverse(SqBiTree T,Status(*Visit)(TElemType))
 { /* 层序遍历二叉树 */
   int i=MAX_TREE_SIZE-1,j;
   while(T[i]==Nil)
     i--; /* 找到最后一个非空结点的序号 */
   for(j=0;j<=i;j++)  /* 从根结点起,按层序遍历二叉树 */
     if(T[j]!=Nil)
       Visit(T[j]); /* 只遍历非空的结点 */
   printf("\n");
 }

 void Print(SqBiTree T)
 { /* 逐层、按本层序号输出二叉树 */
   int j,k;
   position p;
   TElemType e;
   for(j=1;j<=BiTreeDepth(T);j++)
   {
     printf("第%d层: ",j);
     for(k=1;k<=pow(2,j-1);k++)
     {
       p.level=j;
       p.order=k;
       e=Value(T,p);
       if(e!=Nil)
         printf("%d:%d ",k,e);
     }
     printf("\n");
   }
 }

 /* bo6-2.c 二叉树的二叉链表存储(存储结构由c6-2.h定义)的基本操作(22个) */
 Status InitBiTree(BiTree *T)
 { /* 操作结果: 构造空二叉树T */
   *T=NULL;
   return OK;
 }

 void DestroyBiTree(BiTree *T)
 { /* 初始条件: 二叉树T存在。操作结果: 销毁二叉树T */
   if(*T) /* 非空树 */
   {
     if((*T)->lchild) /* 有左孩子 */
       DestroyBiTree(&(*T)->lchild); /* 销毁左孩子子树 */
     if((*T)->rchild) /* 有右孩子 */
       DestroyBiTree(&(*T)->rchild); /* 销毁右孩子子树 */
     free(*T); /* 释放根结点 */
     *T=NULL; /* 空指针赋0 */
   }
 }

 void CreateBiTree(BiTree *T)
 { /* 算法6.4:按先序次序输入二叉树中结点的值（可为字符型或整型，在主程中 */
   /* 定义），构造二叉链表表示的二叉树T。变量Nil表示空（子）树。有改动 */
   TElemType ch;
 #ifdef CHAR
   scanf("%c",&ch);
 #endif
 #ifdef INT
   scanf("%d",&ch);
 #endif
   if(ch==Nil) /* 空 */
     *T=NULL;
   else
   {
     *T=(BiTree)malloc(sizeof(BiTNode));
     if(!*T)
       exit(OVERFLOW);
     (*T)->data=ch; /* 生成根结点 */
     CreateBiTree(&(*T)->lchild); /* 构造左子树 */
     CreateBiTree(&(*T)->rchild); /* 构造右子树 */
   }
 }

 Status BiTreeEmpty(BiTree T)
 { /* 初始条件: 二叉树T存在 */
   /* 操作结果: 若T为空二叉树,则返回TRUE,否则FALSE */
   if(T)
     return FALSE;
   else
     return TRUE;
 }

 #define ClearBiTree DestroyBiTree

 int BiTreeDepth(BiTree T)
 { /* 初始条件: 二叉树T存在。操作结果: 返回T的深度 */
   int i,j;
   if(!T)
     return 0;
   if(T->lchild)
     i=BiTreeDepth(T->lchild);
   else
     i=0;
   if(T->rchild)
     j=BiTreeDepth(T->rchild);
   else
     j=0;
   return i>j?i+1:j+1;
 }

 TElemType Root(BiTree T)
 { /* 初始条件: 二叉树T存在。操作结果: 返回T的根 */
   if(BiTreeEmpty(T))
     return Nil;
   else
     return T->data;
 }

 TElemType Value(BiTree p)
 { /* 初始条件: 二叉树T存在，p指向T中某个结点 */
   /* 操作结果: 返回p所指结点的值 */
   return p->data;
 }

 void Assign(BiTree p,TElemType value)
 { /* 给p所指结点赋值为value */
   p->data=value;
 }

 typedef BiTree QElemType; /* 设队列元素为二叉树的指针类型 */
 #include"c3-2.h"
 #include"bo3-2.c"
 TElemType Parent(BiTree T,TElemType e)
 { /* 初始条件: 二叉树T存在,e是T中某个结点 */
   /* 操作结果: 若e是T的非根结点,则返回它的双亲,否则返回＂空＂ */
   LinkQueue q;
   QElemType a;
   if(T) /* 非空树 */
   {
     InitQueue(&q); /* 初始化队列 */
     EnQueue(&q,T); /* 树根入队 */
     while(!QueueEmpty(q)) /* 队不空 */
     {
       DeQueue(&q,&a); /* 出队,队列元素赋给a */
       if(a->lchild&&a->lchild->data==e||a->rchild&&a->rchild->data==e)
       /* 找到e(是其左或右孩子) */
         return a->data; /* 返回e的双亲的值 */
       else /* 没找到e,则入队其左右孩子指针(如果非空) */
       {
         if(a->lchild)
           EnQueue(&q,a->lchild);
         if(a->rchild)
           EnQueue(&q,a->rchild);
       }
     }
   }
   return Nil; /* 树空或没找到e */
 }

 BiTree Point(BiTree T,TElemType s)
 { /* 返回二叉树T中指向元素值为s的结点的指针。另加 */
   LinkQueue q;
   QElemType a;
   if(T) /* 非空树 */
   {
     InitQueue(&q); /* 初始化队列 */
     EnQueue(&q,T); /* 根结点入队 */
     while(!QueueEmpty(q)) /* 队不空 */
     {
       DeQueue(&q,&a); /* 出队,队列元素赋给a */
       if(a->data==s)
         return a;
       if(a->lchild) /* 有左孩子 */
         EnQueue(&q,a->lchild); /* 入队左孩子 */
       if(a->rchild) /* 有右孩子 */
         EnQueue(&q,a->rchild); /* 入队右孩子 */
     }
   }
   return NULL;
 }

 TElemType LeftChild(BiTree T,TElemType e)
 { /* 初始条件: 二叉树T存在,e是T中某个结点 */
   /* 操作结果: 返回e的左孩子。若e无左孩子,则返回＂空＂ */
   BiTree a;
   if(T) /* 非空树 */
   {
     a=Point(T,e); /* a是结点e的指针 */
     if(a&&a->lchild) /* T中存在结点e且e存在左孩子 */
       return a->lchild->data; /* 返回e的左孩子的值 */
   }
   return Nil; /* 其余情况返回空 */
 }

 TElemType RightChild(BiTree T,TElemType e)
 { /* 初始条件: 二叉树T存在,e是T中某个结点 */
   /* 操作结果: 返回e的右孩子。若e无右孩子,则返回＂空＂ */
   BiTree a;
   if(T) /* 非空树 */
   {
     a=Point(T,e); /* a是结点e的指针 */
     if(a&&a->rchild) /* T中存在结点e且e存在右孩子 */
       return a->rchild->data; /* 返回e的右孩子的值 */
   }
   return Nil; /* 其余情况返回空 */
 }

 TElemType LeftSibling(BiTree T,TElemType e)
 { /* 初始条件: 二叉树T存在,e是T中某个结点 */
   /* 操作结果: 返回e的左兄弟。若e是T的左孩子或无左兄弟,则返回＂空＂ */
   TElemType a;
   BiTree p;
   if(T) /* 非空树 */
   {
     a=Parent(T,e); /* a为e的双亲 */
     p=Point(T,a); /* p为指向结点a的指针 */
     if(p->lchild&&p->rchild&&p->rchild->data==e) /* p存在左右孩子且右孩子是e */
       return p->lchild->data; /* 返回p的左孩子(e的左兄弟) */
   }
   return Nil; /* 树空或没找到e的左兄弟 */
 }

 TElemType RightSibling(BiTree T,TElemType e)
 { /* 初始条件: 二叉树T存在,e是T中某个结点 */
   /* 操作结果: 返回e的右兄弟。若e是T的右孩子或无右兄弟,则返回＂空＂ */
   TElemType a;
   BiTree p;
   if(T) /* 非空树 */
   {
     a=Parent(T,e); /* a为e的双亲 */
     p=Point(T,a); /* p为指向结点a的指针 */
     if(p->lchild&&p->rchild&&p->lchild->data==e) /* p存在左右孩子且左孩子是e */
       return p->rchild->data; /* 返回p的右孩子(e的右兄弟) */
   }
   return Nil; /* 树空或没找到e的右兄弟 */
 }

 Status InsertChild(BiTree p,int LR,BiTree c) /* 形参T无用 */
 { /* 初始条件: 二叉树T存在,p指向T中某个结点,LR为0或1,非空二叉树c与T */
   /*           不相交且右子树为空 */
   /* 操作结果: 根据LR为0或1,插入c为T中p所指结点的左或右子树。p所指结点的 */
   /*           原有左或右子树则成为c的右子树 */
   if(p) /* p不空 */
   {
     if(LR==0)
     {
       c->rchild=p->lchild;
       p->lchild=c;
     }
     else /* LR==1 */
     {
       c->rchild=p->rchild;
       p->rchild=c;
     }
     return OK;
   }
   return ERROR; /* p空 */
 }

 Status DeleteChild(BiTree p,int LR) /* 形参T无用 */
 { /* 初始条件: 二叉树T存在,p指向T中某个结点,LR为0或1 */
   /* 操作结果: 根据LR为0或1,删除T中p所指结点的左或右子树 */
   if(p) /* p不空 */
   {
     if(LR==0) /* 删除左子树 */
       ClearBiTree(&p->lchild);
     else /* 删除右子树 */
       ClearBiTree(&p->rchild);
     return OK;
   }
   return ERROR; /* p空 */
 }

 void PreOrderTraverse(BiTree T,Status(*Visit)(TElemType))
 { /* 初始条件: 二叉树T存在,Visit是对结点操作的应用函数。算法6.1，有改动 */
   /* 操作结果: 先序递归遍历T,对每个结点调用函数Visit一次且仅一次 */
   if(T) /* T不空 */
   {
     Visit(T->data); /* 先访问根结点 */
     PreOrderTraverse(T->lchild,Visit); /* 再先序遍历左子树 */
     PreOrderTraverse(T->rchild,Visit); /* 最后先序遍历右子树 */
   }
 }

 void InOrderTraverse(BiTree T,Status(*Visit)(TElemType))
 { /* 初始条件: 二叉树T存在,Visit是对结点操作的应用函数 */
   /* 操作结果: 中序递归遍历T,对每个结点调用函数Visit一次且仅一次 */
   if(T)
   {
     InOrderTraverse(T->lchild,Visit); /* 先中序遍历左子树 */
     Visit(T->data); /* 再访问根结点 */
     InOrderTraverse(T->rchild,Visit); /* 最后中序遍历右子树 */
   }
 }

 typedef BiTree SElemType; /* 设栈元素为二叉树的指针类型 */
 #include"c3-1.h"
 #include"bo3-1.c"
 Status InOrderTraverse1(BiTree T,Status(*Visit)(TElemType))
 { /* 采用二叉链表存储结构，Visit是对数据元素操作的应用函数。算法6.3 */
   /* 中序遍历二叉树T的非递归算法(利用栈)，对每个数据元素调用函数Visit */
   SqStack S;
   InitStack(&S);
   while(T||!StackEmpty(S))
   {
     if(T)
     { /* 根指针进栈,遍历左子树 */
       Push(&S,T);
       T=T->lchild;
     }
     else
     { /* 根指针退栈,访问根结点,遍历右子树 */
       Pop(&S,&T);
       if(!Visit(T->data))
         return ERROR;
       T=T->rchild;
     }
   }
   printf("\n");
   return OK;
 }

 Status InOrderTraverse2(BiTree T,Status(*Visit)(TElemType))
 { /* 采用二叉链表存储结构，Visit是对数据元素操作的应用函数。算法6.2 */
   /* 中序遍历二叉树T的非递归算法(利用栈)，对每个数据元素调用函数Visit */
   SqStack S;
   BiTree p;
   InitStack(&S);
   Push(&S,T); /* 根指针进栈 */
   while(!StackEmpty(S))
   {
     while(GetTop(S,&p)&&p)
       Push(&S,p->lchild); /* 向左走到尽头 */
     Pop(&S,&p); /* 空指针退栈 */
     if(!StackEmpty(S))
     { /* 访问结点,向右一步 */
       Pop(&S,&p);
       if(!Visit(p->data))
         return ERROR;
       Push(&S,p->rchild);
     }
   }
   printf("\n");
   return OK;
 }

 void PostOrderTraverse(BiTree T,Status(*Visit)(TElemType))
 { /* 初始条件: 二叉树T存在,Visit是对结点操作的应用函数 */
   /* 操作结果: 后序递归遍历T,对每个结点调用函数Visit一次且仅一次 */
   if(T) /* T不空 */
   {
     PostOrderTraverse(T->lchild,Visit); /* 先后序遍历左子树 */
     PostOrderTraverse(T->rchild,Visit); /* 再后序遍历右子树 */
     Visit(T->data); /* 最后访问根结点 */
   }
 }

 void LevelOrderTraverse(BiTree T,Status(*Visit)(TElemType))
 { /* 初始条件：二叉树T存在,Visit是对结点操作的应用函数 */
   /* 操作结果：层序递归遍历T(利用队列),对每个结点调用函数Visit一次且仅一次 */
   LinkQueue q;
   QElemType a;
   if(T)
   {
     InitQueue(&q);
     EnQueue(&q,T);
     while(!QueueEmpty(q))
     {
       DeQueue(&q,&a);
       Visit(a->data);
       if(a->lchild!=NULL)
         EnQueue(&q,a->lchild);
       if(a->rchild!=NULL)
         EnQueue(&q,a->rchild);
     }
     printf("\n");
   }
 }

 /* bo6-3.c 二叉树的二叉线索存储(存储结构由c6-3.h定义)的基本操作 */
 Status CreateBiThrTree(BiThrTree *T)
 { /* 按先序输入二叉线索树中结点的值,构造二叉线索树T */
   /* 0(整型)/空格(字符型)表示空结点 */
   TElemType h;
 #if CHAR
   scanf("%c",&h);
 #else
   scanf("%d",&h);
 #endif
   if(h==Nil)
     *T=NULL;
   else
   {
     *T=(BiThrTree)malloc(sizeof(BiThrNode));
     if(!*T)
       exit(OVERFLOW);
     (*T)->data=h; /* 生成根结点(先序) */
     CreateBiThrTree(&(*T)->lchild); /* 递归构造左子树 */
     if((*T)->lchild) /* 有左孩子 */
       (*T)->LTag=Link;
     CreateBiThrTree(&(*T)->rchild); /* 递归构造右子树 */
     if((*T)->rchild) /* 有右孩子 */
       (*T)->RTag=Link;
   }
   return OK;
 }

 BiThrTree pre; /* 全局变量,始终指向刚刚访问过的结点 */
 void InThreading(BiThrTree p)
 { /* 中序遍历进行中序线索化。算法6.7 */
   if(p)
   {
     InThreading(p->lchild); /* 递归左子树线索化 */
     if(!p->lchild) /* 没有左孩子 */
     {
       p->LTag=Thread; /* 前驱线索 */
       p->lchild=pre; /* 左孩子指针指向前驱 */
     }
     if(!pre->rchild) /* 前驱没有右孩子 */
     {
       pre->RTag=Thread; /* 后继线索 */
       pre->rchild=p; /* 前驱右孩子指针指向后继(当前结点p) */
     }
     pre=p; /* 保持pre指向p的前驱 */
     InThreading(p->rchild); /* 递归右子树线索化 */
   }
 }

 Status InOrderThreading(BiThrTree *Thrt,BiThrTree T)
 { /* 中序遍历二叉树T,并将其中序线索化,Thrt指向头结点。算法6.6 */
   *Thrt=(BiThrTree)malloc(sizeof(BiThrNode));
   if(!*Thrt)
     exit(OVERFLOW);
   (*Thrt)->LTag=Link; /* 建头结点 */
   (*Thrt)->RTag=Thread;
   (*Thrt)->rchild=*Thrt; /* 右指针回指 */
   if(!T) /* 若二叉树空，则左指针回指 */
     (*Thrt)->lchild=*Thrt;
   else
   {
     (*Thrt)->lchild=T;
     pre=*Thrt;
     InThreading(T); /* 中序遍历进行中序线索化 */
     pre->rchild=*Thrt;
     pre->RTag=Thread; /* 最后一个结点线索化 */
     (*Thrt)->rchild=pre;
   }
   return OK;
 }

 Status InOrderTraverse_Thr(BiThrTree T,Status(*Visit)(TElemType))
 { /* 中序遍历二叉线索树T(头结点)的非递归算法。算法6.5 */
   BiThrTree p;
   p=T->lchild; /* p指向根结点 */
   while(p!=T)
   { /* 空树或遍历结束时,p==T */
     while(p->LTag==Link)
       p=p->lchild;
     if(!Visit(p->data)) /* 访问其左子树为空的结点 */
       return ERROR;
     while(p->RTag==Thread&&p->rchild!=T)
     {
       p=p->rchild;
       Visit(p->data); /* 访问后继结点 */
     }
     p=p->rchild;
   }
   return OK;
 }

 /* bo6-4.c 树的双亲表存储(存储结构由c6-4.h定义)的基本操作(14个) */
 Status InitTree(PTree *T)
 { /* 操作结果: 构造空树T */
   (*T).n=0;
   return OK;
 }

 void DestroyTree()
 { /* 由于PTree是定长类型,无法销毁 */
 }

 typedef struct
 {
   int num;
   TElemType name;
 }QElemType; /* 定义队列元素类型 */
 #include"c3-2.h" /* 定义LinkQueue类型 */
 #include"bo3-2.c" /* LinkQueue类型的基本操作 */
 Status CreateTree(PTree *T)
 { /* 操作结果: 构造树T */
   LinkQueue q;
   QElemType p,qq;
   int i=1,j,l;
   char c[MAX_TREE_SIZE]; /* 临时存放孩子结点数组 */
   InitQueue(&q); /* 初始化队列 */
   printf("请输入根结点(字符型,空格为空): ");
   scanf("%c%*c",&(*T).nodes[0].data); /* 根结点序号为0,%*c吃掉回车符 */
   if((*T).nodes[0].data!=Nil) /* 非空树 */
   {
     (*T).nodes[0].parent=-1; /* 根结点无双亲 */
     qq.name=(*T).nodes[0].data;
     qq.num=0;
     EnQueue(&q,qq); /* 入队此结点 */
     while(i/* 数组未满且队不空 */
     {
       DeQueue(&q,&qq); /* 出队一个结点 */
       printf("请按长幼顺序输入结点%c的所有孩子: ",qq.name);
       gets(c);
       l=strlen(c);
       for(j=0;j*T).nodes[i].data=c[j];
         (*T).nodes[i].parent=qq.num;
         p.name=c[j];
         p.num=i;
         EnQueue(&q,p); /* 入队此结点 */
         i++;
       }
     }
     if(i>MAX_TREE_SIZE)
     {
       printf("结点数超过数组容量\n");
       exit(OVERFLOW);
     }
     (*T).n=i;
   }
   else
     (*T).n=0;
   return OK;
 }

 #define ClearTree InitTree /* 二者操作相同 */

 Status TreeEmpty(PTree T)
 { /* 初始条件: 树T存在。操作结果: 若T为空树,则返回TRUE,否则返回FALSE */
   if(T.n)
     return FALSE;
   else
     return TRUE;
 }

 int TreeDepth(PTree T)
 { /* 初始条件: 树T存在。操作结果: 返回T的深度 */
   int k,m,def,max=0;
   for(k=0;k1; /* 初始化本际点的深度 */
     m=T.nodes[k].parent;
     while(m!=-1)
     {
       m=T.nodes[m].parent;
       def++;
     }
     if(maxmax=def;
   }
   return max; /* 最大深度 */
 }

 TElemType Root(PTree T)
 { /* 初始条件: 树T存在。操作结果: 返回T的根 */
   int i;
   for(i=0;iif(T.nodes[i].parent<0)
       return T.nodes[i].data;
   return Nil;
 }

 TElemType Value(PTree T,int i)
 { /* 初始条件: 树T存在,i是树T中结点的序号。操作结果: 返回第i个结点的值 */
   if(ireturn T.nodes[i].data;
   else
     return Nil;
 }

 Status Assign(PTree *T,TElemType cur_e,TElemType value)
 { /* 初始条件: 树T存在,cur_e是树T中结点的值。操作结果: 改cur_e为value */
   int j;
   for(j=0;j<(*T).n;j++)
   {
     if((*T).nodes[j].data==cur_e)
     {
       (*T).nodes[j].data=value;
       return OK;
     }
   }
   return ERROR;
 }

 TElemType Parent(PTree T,TElemType cur_e)
 { /* 初始条件: 树T存在,cur_e是T中某个结点 */
   /* 操作结果: 若cur_e是T的非根结点,则返回它的双亲,否则函数值为＂空＂ */
   int j;
   for(j=1;j/* 根结点序号为0 */
     if(T.nodes[j].data==cur_e)
       return T.nodes[T.nodes[j].parent].data;
   return Nil;
 }

 TElemType LeftChild(PTree T,TElemType cur_e)
 { /* 初始条件: 树T存在,cur_e是T中某个结点 */
   /* 操作结果: 若cur_e是T的非叶子结点,则返回它的最左孩子,否则返回＂空＂ */
   int i,j;
   for(i=0;iif(T.nodes[i].data==cur_e) /* 找到cur_e,其序号为i */
       break;
   for(j=i+1;j/* 根据树的构造函数,孩子的序号＞其双亲的序号 */
     if(T.nodes[j].parent==i) /* 根据树的构造函数,最左孩子(长子)的序号＜其它孩子的序号 */
       return T.nodes[j].data;
   return Nil;
 }

 TElemType RightSibling(PTree T,TElemType cur_e)
 { /* 初始条件: 树T存在,cur_e是T中某个结点 */
   /* 操作结果: 若cur_e有右(下一个)兄弟,则返回它的右兄弟,否则返回＂空＂ */
   int i;
   for(i=0;iif(T.nodes[i].data==cur_e) /* 找到cur_e,其序号为i */
       break;
   if(T.nodes[i+1].parent==T.nodes[i].parent)
   /* 根据树的构造函数,若cur_e有右兄弟的话则右兄弟紧接其后 */
     return T.nodes[i+1].data;
   return Nil;
 }

 Status Print(PTree T)
 { /* 输出树T。加 */
   int i;
   printf("结点个数=%d\n",T.n);
   printf(" 结点 双亲\n");
   for(i=0;i"    %c",Value(T,i)); /* 结点 */
     if(T.nodes[i].parent>=0) /* 有双亲 */
       printf("    %c",Value(T,T.nodes[i].parent)); /* 双亲 */
     printf("\n");
   }
   return OK;
 }

 Status InsertChild(PTree *T,TElemType p,int i,PTree c)
 { /* 初始条件: 树T存在,p是T中某个结点,1≤i≤p所指结点的度+1,非空树c与T不相交 */
   /* 操作结果: 插入c为T中p结点的第i棵子树 */
   int j,k,l,f=1,n=0; /* 设交换标志f的初值为1,p的孩子数n的初值为0 */
   PTNode t;
   if(!TreeEmpty(*T)) /* T不空 */
   {
     for(j=0;j<(*T).n;j++) /* 在T中找p的序号 */
       if((*T).nodes[j].data==p) /* p的序号为j */
         break;
     l=j+1; /* 如果c是p的第1棵子树,则插在j+1处 */
     if(i>1) /* c不是p的第1棵子树 */
     {
       for(k=j+1;k<(*T).n;k++) /* 从j+1开始找p的前i-1个孩子 */
         if((*T).nodes[k].parent==j) /* 当前结点是p的孩子 */
         {
           n++; /* 孩子数加1 */
           if(n==i-1) /* 找到p的第i-1个孩子,其序号为k1 */
             break;
         }
       l=k+1; /* c插在k+1处 */
     } /* p的序号为j,c插在l处 */
     if(l<(*T).n) /* 插入点l不在最后 */
       for(k=(*T).n-1;k>=l;k--) /* 依次将序号l以后的结点向后移c.n个位置 */
       {
         (*T).nodes[k+c.n]=(*T).nodes[k];
         if((*T).nodes[k].parent>=l)
           (*T).nodes[k+c.n].parent+=c.n;
       }
     for(k=0;k*T).nodes[l+k].data=c.nodes[k].data; /* 依次将树c的所有结点插于此处 */
       (*T).nodes[l+k].parent=c.nodes[k].parent+l;
     }
     (*T).nodes[l].parent=j; /* 树c的根结点的双亲为p */
     (*T).n+=c.n; /* 树T的结点数加c.n个 */
     while(f)
     { /* 从插入点之后,将结点仍按层序排列 */
       f=0; /* 交换标志置0 */
       for(j=l;j<(*T).n-1;j++)
         if((*T).nodes[j].parent>(*T).nodes[j+1].parent)
         {/* 如果结点j的双亲排在结点j+1的双亲之后(树没有按层序排列),交换两结点*/
           t=(*T).nodes[j];
           (*T).nodes[j]=(*T).nodes[j+1];
           (*T).nodes[j+1]=t;
           f=1; /* 交换标志置1 */
           for(k=j;k<(*T).n;k++) /* 改变双亲序号 */
             if((*T).nodes[k].parent==j)
               (*T).nodes[k].parent++; /* 双亲序号改为j+1 */
             else if((*T).nodes[k].parent==j+1)
               (*T).nodes[k].parent--; /* 双亲序号改为j */
         }
     }
     return OK;
   }
   else /* 树T不存在 */
     return ERROR;
 }

 Status deleted[MAX_TREE_SIZE+1]; /* 删除标志数组(全局量) */
 void DeleteChild(PTree *T,TElemType p,int i)
 { /* 初始条件: 树T存在,p是T中某个结点,1≤i≤p所指结点的度 */
   /* 操作结果: 删除T中结点p的第i棵子树 */
   int j,k,n=0;
   LinkQueue q;
   QElemType pq,qq;
   for(j=0;j<=(*T).n;j++)
     deleted[j]=0; /* 置初值为0(不删除标记) */
   pq.name='a'; /* 此成员不用 */
   InitQueue(&q); /* 初始化队列 */
   for(j=0;j<(*T).n;j++)
     if((*T).nodes[j].data==p)
       break; /* j为结点p的序号 */
   for(k=j+1;k<(*T).n;k++)
   {
     if((*T).nodes[k].parent==j)
       n++;
     if(n==i)
       break; /* k为p的第i棵子树结点的序号 */
   }
   if(k<(*T).n) /* p的第i棵子树结点存在 */
   {
     n=0;
     pq.num=k;
     deleted[k]=1; /* 置删除标记 */
     n++;
     EnQueue(&q,pq);
     while(!QueueEmpty(q))
     {
       DeQueue(&q,&qq);
       for(j=qq.num+1;j<(*T).n;j++)
         if((*T).nodes[j].parent==qq.num)
         {
           pq.num=j;
           deleted[j]=1; /* 置删除标记 */
           n++;
           EnQueue(&q,pq);
         }
     }
     for(j=0;j<(*T).n;j++)
       if(deleted[j]==1)
       {
         for(k=j+1;k<=(*T).n;k++)
         {
           deleted[k-1]=deleted[k];
           (*T).nodes[k-1]=(*T).nodes[k];
           if((*T).nodes[k].parent>j)
             (*T).nodes[k-1].parent--;
         }
         j--;
       }
     (*T).n-=n; /* n为待删除结点数 */
   }
 }

 void TraverseTree(PTree T,void(*Visit)(TElemType))
 { /* 初始条件:二叉树T存在,Visit是对结点操作的应用函数 */
   /* 操作结果:层序遍历树T,对每个结点调用函数Visit一次且仅一次 */
   int i;
   for(i=0;i"\n");
 }

 /* bo6-5.c 树的二叉链表(孩子－兄弟)存储(存储结构由c6-5.h定义)的基本操作(17个) */
 Status InitTree(CSTree *T)
 { /* 操作结果: 构造空树T */
   *T=NULL;
   return OK;
 }

 void DestroyTree(CSTree *T)
 { /* 初始条件: 树T存在。操作结果: 销毁树T */
   if(*T)
   {
     if((*T)->firstchild) /* T有长子 */
       DestroyTree(&(*T)->firstchild); /* 销毁T的长子为根结点的子树 */
     if((*T)->nextsibling) /* T有下一个兄弟 */
       DestroyTree(&(*T)->nextsibling); /* 销毁T的下一个兄弟为根结点的子树 */
     free(*T); /* 释放根结点 */
     *T=NULL;
   }
 }

 typedef CSTree QElemType; /* 定义队列元素类型 */
 #include"c3-2.h" /* 定义LinkQueue类型 */
 #include"bo3-2.c" /* LinkQueue类型的基本操作 */
 Status CreateTree(CSTree *T)
 { /* 构造树T */
   char c[20]; /* 临时存放孩子结点(设不超过20个)的值 */
   CSTree p,p1;
   LinkQueue q;
   int i,l;
   InitQueue(&q);
   printf("请输入根结点(字符型,空格为空): ");
   scanf("%c%*c",&c[0]);
   if(c[0]!=Nil) /* 非空树 */
   {
     *T=(CSTree)malloc(sizeof(CSNode)); /* 建立根结点 */
     (*T)->data=c[0];
     (*T)->nextsibling=NULL;
     EnQueue(&q,*T); /* 入队根结点的指针 */
     while(!QueueEmpty(q)) /* 队不空 */
     {
       DeQueue(&q,&p); /* 出队一个结点的指针 */
       printf("请按长幼顺序输入结点%c的所有孩子: ",p->data);
       gets(c);
       l=strlen(c);
       if(l>0) /* 有孩子 */
       {
         p1=p->firstchild=(CSTree)malloc(sizeof(CSNode)); /* 建立长子结点 */
         p1->data=c[0];
         for(i=1;inextsibling=(CSTree)malloc(sizeof(CSNode)); /* 建立下一个兄弟结点 */
           EnQueue(&q,p1); /* 入队上一个结点 */
           p1=p1->nextsibling;
           p1->data=c[i];
         }
         p1->nextsibling=NULL;
         EnQueue(&q,p1); /* 入队最后一个结点 */
       }
       else
         p->firstchild=NULL;
     }
   }
   else
     *T=NULL;
   return OK;
 }

 #define ClearTree DestroyTree /* 二者操作相同 */

 Status TreeEmpty(CSTree T)
 { /* 初始条件: 树T存在。操作结果: 若T为空树,则返回TURE,否则返回FALSE */
   if(T) /* T不空 */
     return FALSE;
   else
     return TRUE;
 }

 int TreeDepth(CSTree T)
 { /* 初始条件: 树T存在。操作结果: 返回T的深度 */
   CSTree p;
   int depth,max=0;
   if(!T) /* 树空 */
     return 0;
   if(!T->firstchild) /* 树无长子 */
     return 1;
   for(p=T->firstchild;p;p=p->nextsibling)
   {
     depth=TreeDepth(p);
     if(depth>max)
       max=depth;
   }
   return max+1;
 }

 TElemType Value(CSTree p)
 { /* 返回p所指结点的值 */
   return p->data;
 }

 TElemType Root(CSTree T)
 { /* 初始条件: 树T存在。操作结果: 返回T的根 */
   if(T)
     return Value(T);
   else
     return Nil;
 }

 CSTree Point(CSTree T,TElemType s)
 { /* 返回二叉链表(孩子－兄弟)树T中指向元素值为s的结点的指针。另加 */
   LinkQueue q;
   QElemType a;
   if(T) /* 非空树 */
   {
     InitQueue(&q); /* 初始化队列 */
     EnQueue(&q,T); /* 根结点入队 */
     while(!QueueEmpty(q)) /* 队不空 */
     {
       DeQueue(&q,&a); /* 出队,队列元素赋给a */
       if(a->data==s)
     return a;
       if(a->firstchild) /* 有长子 */
         EnQueue(&q,a->firstchild); /* 入队长子 */
       if(a->nextsibling) /* 有下一个兄弟 */
         EnQueue(&q,a->nextsibling); /* 入队下一个兄弟 */
     }
   }
   return NULL;
 }

 Status Assign(CSTree *T,TElemType cur_e,TElemType value)
 { /* 初始条件: 树T存在,cur_e是树T中结点的值。操作结果: 改cur_e为value */
   CSTree p;
   if(*T) /* 非空树 */
   {
     p=Point(*T,cur_e); /* p为cur_e的指针 */
     if(p) /* 找到cur_e */
     {
       p->data=value; /* 赋新值 */
       return OK;
     }
   }
   return Nil; /* 树空或没找到 */
 }

 TElemType Parent(CSTree T,TElemType cur_e)
 { /* 初始条件: 树T存在,cur_e是T中某个结点 */
   /* 操作结果: 若cur_e是T的非根结点,则返回它的双亲,否则函数值为＂空＂ */
   CSTree p,t;
   LinkQueue q;
   InitQueue(&q);
   if(T) /* 树非空 */
   {
     if(Value(T)==cur_e) /* 根结点值为cur_e */
       return Nil;
     EnQueue(&q,T); /* 根结点入队 */
     while(!QueueEmpty(q))
     {
       DeQueue(&q,&p);
       if(p->firstchild) /* p有长子 */
       {
         if(p->firstchild->data==cur_e) /* 长子为cur_e */
           return Value(p); /* 返回双亲 */
         t=p; /* 双亲指针赋给t */
         p=p->firstchild; /* p指向长子 */
         EnQueue(&q,p); /* 入队长子 */
         while(p->nextsibling) /* 有下一个兄弟 */
         {
           p=p->nextsibling; /* p指向下一个兄弟 */
       if(Value(p)==cur_e) /* 下一个兄弟为cur_e */
         return Value(t); /* 返回双亲 */
       EnQueue(&q,p); /* 入队下一个兄弟 */
     }
       }
     }
   }
   return Nil; /* 树空或没找到cur_e */
 }

 TElemType LeftChild(CSTree T,TElemType cur_e)
 { /* 初始条件: 树T存在,cur_e是T中某个结点 */
   /* 操作结果: 若cur_e是T的非叶子结点,则返回它的最左孩子,否则返回＂空＂ */
   CSTree f;
   f=Point(T,cur_e); /* f指向结点cur_e */
   if(f&&f->firstchild) /* 找到结点cur_e且结点cur_e有长子 */
     return f->firstchild->data;
   else
     return Nil;
 }

 TElemType RightSibling(CSTree T,TElemType cur_e)
 { /* 初始条件: 树T存在,cur_e是T中某个结点 */
   /* 操作结果: 若cur_e有右兄弟,则返回它的右兄弟,否则返回＂空＂ */
   CSTree f;
   f=Point(T,cur_e); /* f指向结点cur_e */
   if(f&&f->nextsibling) /* 找到结点cur_e且结点cur_e有右兄弟 */
     return f->nextsibling->data;
   else
     return Nil; /* 树空 */
 }

 Status InsertChild(CSTree *T,CSTree p,int i,CSTree c)
 { /* 初始条件: 树T存在,p指向T中某个结点,1≤i≤p所指结点的度+1,非空树c与T不相交 */
   /* 操作结果: 插入c为T中p结点的第i棵子树 */
   /* 因为p所指结点的地址不会改变，故p不需是引用类型 */
   int j;
   if(*T) /* T不空 */
   {
     if(i==1) /* 插入c为p的长子 */
     {
       c->nextsibling=p->firstchild; /* p的原长子现是c的下一个兄弟(c本无兄弟) */
       p->firstchild=c;
     }
     else /* 找插入点 */
     {
       p=p->firstchild; /* 指向p的长子 */
       j=2;
       while(p&&jnextsibling;
         j++;
       }
       if(j==i) /* 找到插入位置 */
       {
         c->nextsibling=p->nextsibling;
         p->nextsibling=c;
       }
       else /* p原有孩子数小于i-1 */
         return ERROR;
     }
     return OK;
   }
   else /* T空 */
     return ERROR;
 }

 Status DeleteChild(CSTree *T,CSTree p,int i)
 { /* 初始条件: 树T存在,p指向T中某个结点,1≤i≤p所指结点的度 */
   /* 操作结果: 删除T中p所指结点的第i棵子树 */
   /* 因为p所指结点的地址不会改变，故p不需是引用类型 */
   CSTree b;
   int j;
   if(*T) /* T不空 */
   {
     if(i==1) /* 删除长子 */
     {
       b=p->firstchild;
       p->firstchild=b->nextsibling; /* p的原次子现是长子 */
       b->nextsibling=NULL;
       DestroyTree(&b);
     }
     else /* 删除非长子 */
     {
       p=p->firstchild; /* p指向长子 */
       j=2;
       while(p&&jnextsibling;
         j++;
       }
       if(j==i) /* 找到第i棵子树 */
       {
         b=p->nextsibling;
         p->nextsibling=b->nextsibling;
         b->nextsibling=NULL;
         DestroyTree(&b);
       }
       else /* p原有孩子数小于i */
         return ERROR;
     }
     return OK;
   }
   else
     return ERROR;
 }

 void PreOrderTraverse(CSTree T,void(*Visit)(TElemType))
 { /* 先根遍历孩子－兄弟二叉链表结构的树T */
   if(T)
   {
     Visit(Value(T)); /* 先访问根结点 */
     PreOrderTraverse(T->firstchild,Visit); /* 再先根遍历长子子树 */
     PreOrderTraverse(T->nextsibling,Visit); /* 最后先根遍历下一个兄弟子树 */
   }
 }

 void PostOrderTraverse(CSTree T,void(*Visit)(TElemType))
 { /* 后根遍历孩子－兄弟二叉链表结构的树T */
   CSTree p;
   if(T)
   {
     if(T->firstchild) /* 有长子 */
     {
       PostOrderTraverse(T->firstchild,Visit); /* 后根遍历长子子树 */
       p=T->firstchild->nextsibling; /* p指向长子的下一个兄弟 */
       while(p)
       {
         PostOrderTraverse(p,Visit); /* 后根遍历下一个兄弟子树 */
         p=p->nextsibling; /* p指向再下一个兄弟 */
       }
     }
     Visit(Value(T)); /* 最后访问根结点 */
   }
 }

 void LevelOrderTraverse(CSTree T,void(*Visit)(TElemType))
 { /* 层序遍历孩子－兄弟二叉链表结构的树T */
   CSTree p;
   LinkQueue q;
   InitQueue(&q);
   if(T)
   {
     Visit(Value(T)); /* 先访问根结点 */
     EnQueue(&q,T); /* 入队根结点的指针 */
     while(!QueueEmpty(q)) /* 队不空 */
     {
       DeQueue(&q,&p); /* 出队一个结点的指针 */
       if(p->firstchild) /* 有长子 */
       {
         p=p->firstchild;
         Visit(Value(p)); /* 访问长子结点 */
         EnQueue(&q,p); /* 入队长子结点的指针 */
         while(p->nextsibling) /* 有下一个兄弟 */
         {
           p=p->nextsibling;
           Visit(Value(p)); /* 访问下一个兄弟 */
           EnQueue(&q,p); /* 入队兄弟结点的指针 */
         }
       }
     }
   }
 }

 /* bo6-5.c 树的二叉链表(孩子－兄弟)存储(存储结构由c6-5.h定义)的基本操作(17个) */
 Status InitTree(CSTree *T)
 { /* 操作结果: 构造空树T */
   *T=NULL;
   return OK;
 }

 void DestroyTree(CSTree *T)
 { /* 初始条件: 树T存在。操作结果: 销毁树T */
   if(*T)
   {
     if((*T)->firstchild) /* T有长子 */
       DestroyTree(&(*T)->firstchild); /* 销毁T的长子为根结点的子树 */
     if((*T)->nextsibling) /* T有下一个兄弟 */
       DestroyTree(&(*T)->nextsibling); /* 销毁T的下一个兄弟为根结点的子树 */
     free(*T); /* 释放根结点 */
     *T=NULL;
   }
 }

 typedef CSTree QElemType; /* 定义队列元素类型 */
 #include"c3-2.h" /* 定义LinkQueue类型 */
 #include"bo3-2.c" /* LinkQueue类型的基本操作 */
 Status CreateTree(CSTree *T)
 { /* 构造树T */
   char c[20]; /* 临时存放孩子结点(设不超过20个)的值 */
   CSTree p,p1;
   LinkQueue q;
   int i,l;
   InitQueue(&q);
   printf("请输入根结点(字符型,空格为空): ");
   scanf("%c%*c",&c[0]);
   if(c[0]!=Nil) /* 非空树 */
   {
     *T=(CSTree)malloc(sizeof(CSNode)); /* 建立根结点 */
     (*T)->data=c[0];
     (*T)->nextsibling=NULL;
     EnQueue(&q,*T); /* 入队根结点的指针 */
     while(!QueueEmpty(q)) /* 队不空 */
     {
       DeQueue(&q,&p); /* 出队一个结点的指针 */
       printf("请按长幼顺序输入结点%c的所有孩子: ",p->data);
       gets(c);
       l=strlen(c);
       if(l>0) /* 有孩子 */
       {
         p1=p->firstchild=(CSTree)malloc(sizeof(CSNode)); /* 建立长子结点 */
         p1->data=c[0];
         for(i=1;inextsibling=(CSTree)malloc(sizeof(CSNode)); /* 建立下一个兄弟结点 */
           EnQueue(&q,p1); /* 入队上一个结点 */
           p1=p1->nextsibling;
           p1->data=c[i];
         }
         p1->nextsibling=NULL;
         EnQueue(&q,p1); /* 入队最后一个结点 */
       }
       else
         p->firstchild=NULL;
     }
   }
   else
     *T=NULL;
   return OK;
 }

 #define ClearTree DestroyTree /* 二者操作相同 */

 Status TreeEmpty(CSTree T)
 { /* 初始条件: 树T存在。操作结果: 若T为空树,则返回TURE,否则返回FALSE */
   if(T) /* T不空 */
     return FALSE;
   else
     return TRUE;
 }

 int TreeDepth(CSTree T)
 { /* 初始条件: 树T存在。操作结果: 返回T的深度 */
   CSTree p;
   int depth,max=0;
   if(!T) /* 树空 */
     return 0;
   if(!T->firstchild) /* 树无长子 */
     return 1;
   for(p=T->firstchild;p;p=p->nextsibling)
   {
     depth=TreeDepth(p);
     if(depth>max)
       max=depth;
   }
   return max+1;
 }

 TElemType Value(CSTree p)
 { /* 返回p所指结点的值 */
   return p->data;
 }

 TElemType Root(CSTree T)
 { /* 初始条件: 树T存在。操作结果: 返回T的根 */
   if(T)
     return Value(T);
   else
     return Nil;
 }

 CSTree Point(CSTree T,TElemType s)
 { /* 返回二叉链表(孩子－兄弟)树T中指向元素值为s的结点的指针。另加 */
   LinkQueue q;
   QElemType a;
   if(T) /* 非空树 */
   {
     InitQueue(&q); /* 初始化队列 */
     EnQueue(&q,T); /* 根结点入队 */
     while(!QueueEmpty(q)) /* 队不空 */
     {
       DeQueue(&q,&a); /* 出队,队列元素赋给a */
       if(a->data==s)
     return a;
       if(a->firstchild) /* 有长子 */
         EnQueue(&q,a->firstchild); /* 入队长子 */
       if(a->nextsibling) /* 有下一个兄弟 */
         EnQueue(&q,a->nextsibling); /* 入队下一个兄弟 */
     }
   }
   return NULL;
 }

 Status Assign(CSTree *T,TElemType cur_e,TElemType value)
 { /* 初始条件: 树T存在,cur_e是树T中结点的值。操作结果: 改cur_e为value */
   CSTree p;
   if(*T) /* 非空树 */
   {
     p=Point(*T,cur_e); /* p为cur_e的指针 */
     if(p) /* 找到cur_e */
     {
       p->data=value; /* 赋新值 */
       return OK;
     }
   }
   return Nil; /* 树空或没找到 */
 }

 TElemType Parent(CSTree T,TElemType cur_e)
 { /* 初始条件: 树T存在,cur_e是T中某个结点 */
   /* 操作结果: 若cur_e是T的非根结点,则返回它的双亲,否则函数值为＂空＂ */
   CSTree p,t;
   LinkQueue q;
   InitQueue(&q);
   if(T) /* 树非空 */
   {
     if(Value(T)==cur_e) /* 根结点值为cur_e */
       return Nil;
     EnQueue(&q,T); /* 根结点入队 */
     while(!QueueEmpty(q))
     {
       DeQueue(&q,&p);
       if(p->firstchild) /* p有长子 */
       {
         if(p->firstchild->data==cur_e) /* 长子为cur_e */
           return Value(p); /* 返回双亲 */
         t=p; /* 双亲指针赋给t */
         p=p->firstchild; /* p指向长子 */
         EnQueue(&q,p); /* 入队长子 */
         while(p->nextsibling) /* 有下一个兄弟 */
         {
           p=p->nextsibling; /* p指向下一个兄弟 */
       if(Value(p)==cur_e) /* 下一个兄弟为cur_e */
         return Value(t); /* 返回双亲 */
       EnQueue(&q,p); /* 入队下一个兄弟 */
     }
       }
     }
   }
   return Nil; /* 树空或没找到cur_e */
 }

 TElemType LeftChild(CSTree T,TElemType cur_e)
 { /* 初始条件: 树T存在,cur_e是T中某个结点 */
   /* 操作结果: 若cur_e是T的非叶子结点,则返回它的最左孩子,否则返回＂空＂ */
   CSTree f;
   f=Point(T,cur_e); /* f指向结点cur_e */
   if(f&&f->firstchild) /* 找到结点cur_e且结点cur_e有长子 */
     return f->firstchild->data;
   else
     return Nil;
 }

 TElemType RightSibling(CSTree T,TElemType cur_e)
 { /* 初始条件: 树T存在,cur_e是T中某个结点 */
   /* 操作结果: 若cur_e有右兄弟,则返回它的右兄弟,否则返回＂空＂ */
   CSTree f;
   f=Point(T,cur_e); /* f指向结点cur_e */
   if(f&&f->nextsibling) /* 找到结点cur_e且结点cur_e有右兄弟 */
     return f->nextsibling->data;
   else
     return Nil; /* 树空 */
 }

 Status InsertChild(CSTree *T,CSTree p,int i,CSTree c)
 { /* 初始条件: 树T存在,p指向T中某个结点,1≤i≤p所指结点的度+1,非空树c与T不相交 */
   /* 操作结果: 插入c为T中p结点的第i棵子树 */
   /* 因为p所指结点的地址不会改变，故p不需是引用类型 */
   int j;
   if(*T) /* T不空 */
   {
     if(i==1) /* 插入c为p的长子 */
     {
       c->nextsibling=p->firstchild; /* p的原长子现是c的下一个兄弟(c本无兄弟) */
       p->firstchild=c;
     }
     else /* 找插入点 */
     {
       p=p->firstchild; /* 指向p的长子 */
       j=2;
       while(p&&jnextsibling;
         j++;
       }
       if(j==i) /* 找到插入位置 */
       {
         c->nextsibling=p->nextsibling;
         p->nextsibling=c;
       }
       else /* p原有孩子数小于i-1 */
         return ERROR;
     }
     return OK;
   }
   else /* T空 */
     return ERROR;
 }

 Status DeleteChild(CSTree *T,CSTree p,int i)
 { /* 初始条件: 树T存在,p指向T中某个结点,1≤i≤p所指结点的度 */
   /* 操作结果: 删除T中p所指结点的第i棵子树 */
   /* 因为p所指结点的地址不会改变，故p不需是引用类型 */
   CSTree b;
   int j;
   if(*T) /* T不空 */
   {
     if(i==1) /* 删除长子 */
     {
       b=p->firstchild;
       p->firstchild=b->nextsibling; /* p的原次子现是长子 */
       b->nextsibling=NULL;
       DestroyTree(&b);
     }
     else /* 删除非长子 */
     {
       p=p->firstchild; /* p指向长子 */
       j=2;
       while(p&&jnextsibling;
         j++;
       }
       if(j==i) /* 找到第i棵子树 */
       {
         b=p->nextsibling;
         p->nextsibling=b->nextsibling;
         b->nextsibling=NULL;
         DestroyTree(&b);
       }
       else /* p原有孩子数小于i */
         return ERROR;
     }
     return OK;
   }
   else
     return ERROR;
 }

 void PreOrderTraverse(CSTree T,void(*Visit)(TElemType))
 { /* 先根遍历孩子－兄弟二叉链表结构的树T */
   if(T)
   {
     Visit(Value(T)); /* 先访问根结点 */
     PreOrderTraverse(T->firstchild,Visit); /* 再先根遍历长子子树 */
     PreOrderTraverse(T->nextsibling,Visit); /* 最后先根遍历下一个兄弟子树 */
   }
 }

 void PostOrderTraverse(CSTree T,void(*Visit)(TElemType))
 { /* 后根遍历孩子－兄弟二叉链表结构的树T */
   CSTree p;
   if(T)
   {
     if(T->firstchild) /* 有长子 */
     {
       PostOrderTraverse(T->firstchild,Visit); /* 后根遍历长子子树 */
       p=T->firstchild->nextsibling; /* p指向长子的下一个兄弟 */
       while(p)
       {
         PostOrderTraverse(p,Visit); /* 后根遍历下一个兄弟子树 */
         p=p->nextsibling; /* p指向再下一个兄弟 */
       }
     }
     Visit(Value(T)); /* 最后访问根结点 */
   }
 }

 void LevelOrderTraverse(CSTree T,void(*Visit)(TElemType))
 { /* 层序遍历孩子－兄弟二叉链表结构的树T */
   CSTree p;
   LinkQueue q;
   InitQueue(&q);
   if(T)
   {
     Visit(Value(T)); /* 先访问根结点 */
     EnQueue(&q,T); /* 入队根结点的指针 */
     while(!QueueEmpty(q)) /* 队不空 */
     {
       DeQueue(&q,&p); /* 出队一个结点的指针 */
       if(p->firstchild) /* 有长子 */
       {
         p=p->firstchild;
         Visit(Value(p)); /* 访问长子结点 */
         EnQueue(&q,p); /* 入队长子结点的指针 */
         while(p->nextsibling) /* 有下一个兄弟 */
         {
           p=p->nextsibling;
           Visit(Value(p)); /* 访问下一个兄弟 */
           EnQueue(&q,p); /* 入队兄弟结点的指针 */
         }
       }
     }
   }
 }

第五部分：mian6-1.c运行结果


实际运行结果：