求解二分图的最大匹配的匈牙利算法---POJ 1325 Machine Schedule

【基本概念】

二分图：简单来说，如果图中点可以被分为两组，并且使得所有边都跨越组的边界，则这就是一个二分图。准确地说：把一个图的顶点划分为两个不相交集 U 和V ，使得每一条边都分别连接U、V中的顶点。如果存在这样的划分，则此图为一个二分图。

匹配：在图论中，一个「匹配」（matching）是一个边的集合，其中任意两条边都没有公共顶点。匹配其实是边独立集。显然，在二分图中的匹配就相当于对两组点进行匹配。

完美匹配：对于一个图G 与给定的一个匹配M，如果图G 中不存在M 的未盖点，则称匹配M 为图G 的完美匹配。

最大匹配：一个图所有匹配中，所含匹配边数最多的匹配，称为这个图的最大匹配。

举例来说：如下图所示，如果在某一对男孩和女孩之间存在相连的边，就意味着他们彼此喜欢。是否可能让所有男孩和女孩两两配对，使得每对儿都互相喜欢呢？图论中，这就是完美匹配问题。如果换一个说法：最多有多少互相喜欢的男孩/女孩可以配对儿？这就是最大匹配问题。

【求解算法】

求二部图最大匹配的算法有：

(1) 网络流解法 

(2) 匈牙利算法

(3) Hopcroft-Karp 算法（匈牙利算法的改进）。

1.网络流解法

---摘自《图论算法理论、实现及应用 》

(1)基本原理：

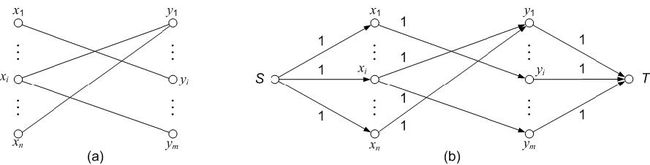
设二部图为G(V, E)，它的顶点集合V 所包含的两个子集为X = { x1, x2, …, xm }和Y = { y1, y2, …,yn }，如下图(a)所示。如果把二部图中看成一个网络，边(xi, yk)都看成有向边，则在求最大匹配时要保证从顶点xi 发出的边最多只选一条、进入顶点yk 的边最多也只选一条，在这些前提下将尽可能多的边选入到匹配中来。

设想有一个源点S，控制从S 到xi 的弧的容量为1，这样就能保证从顶点xi 发出的边最多只选一条。同样，设想有一个汇点T，控制从顶点yk 到T 的弧的容量也为1，这样就能保证进入顶点yk 的边最多也只选一条。另外，设边的容量也为1。

按照上述思路构造好容量网络后，任意一条从S 到T 的路径，一定具有S−xi−yk−T 的形式，且这条路径上3 条弧、、的容量均为1。因此，该容量网络的最大流中每条从S 到T 的路径上，中间这一条边的集合就构成了二部图的最大匹配。

(2)网络流的构造

  1. 求二部图最大匹配的容量网络构造和求解方法如下：从二部图G 出发构造一个容量网络G´，步骤如下：

• a) 增加一个源点S 和汇点T；

• b) 从S 向X 的每一个顶点都画一条有向弧，从Y 的每一个顶点都向T 画一条有向弧；

• c) 原来G 中的边都改成有向弧，方向是从X 的顶点指向Y 的顶点；

• d) 令所有弧的容量都等于1。构造好的流量网络如下图(b)所示。

  2. 求容量网络G´的最大流F。 

  3.最大流F 求解完毕后，从X 的顶点指向Y 的顶点的弧集合中，弧流量为1 的弧对应二部图最大匹配中的边，最大流F 的流量对应二部图的最大匹配的边数。

下图表示了一个网络流构造方法的实例：

(3)算法复杂度

取决于网络流算法。

2.匈牙利算法

(0)基本概念：

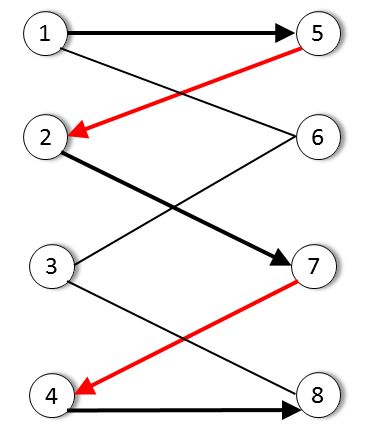
交替轨：又称交替路。从一个未匹配点出发，依次经过非匹配边、匹配边、非匹配边…形成的路径叫交替轨。特别地，如果轨P 仅含一条边，那么无论这条边是否属于匹配M，P 一定是一条交替路。

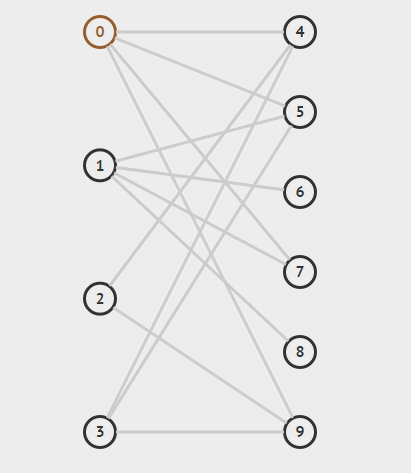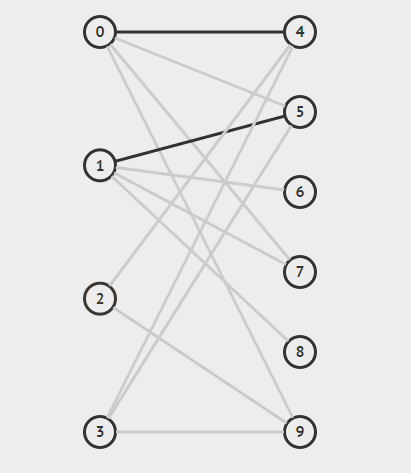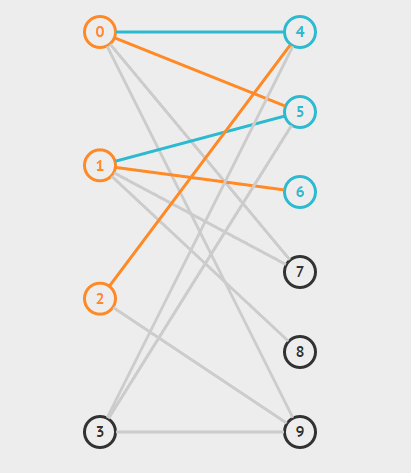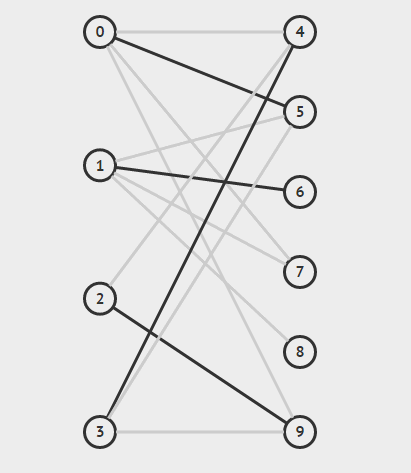
可增广轨：又称可增广路。对于一个给定的图G 和匹配M，两个端点都是未盖点（不与匹配中的任意一条边关联，即没有匹配的点）的交错轨称为关于M 的可增广轨。

在上图中1->5->2->7->4->8就是一条增广轨。

为什么这样的轨是可增广轨？

增广路有一个重要特点：非匹配边比匹配边多一条。因此，研究增广路的意义是改进匹配。只要把增广路中的匹配边和非匹配边的身份交换即可。由于中间的匹配节点不存在其他相连的匹配边，所以这样做不会破坏匹配的性质。交换后，图中的匹配边数目比原来多了 1 条。

(1)基本原理：

从当前匹配M（如果没有匹配，则取初始匹配为M＝Ø）出发，检查每一个未盖点，然后从它出发寻找可增广路，找到可增广路，则沿着这条可增广路进行扩充，直到不存在可增广路为止。

根据搜索增广路方式的不同可以分为：（1）DFS增广（2）BFS增广（3）多路增广

下面主要介绍DFS增广，因为DFS增广好理解而且代码量少。

算法最基本流程：

1. 置边集M为空（初始化，谁和谁都没连着）

1. 选择一个新的原点寻找增广路

1. 重复(2)操作直到找不出增广路径为止（2，3步骤构成一个循环）

伪代码：（来源： https://www.byvoid.com/blog/hungary）

bool 寻找从k出发的对应项出的可增广路
{
    while (从邻接表中列举k能关联到顶点j)
    {
        if (j不在增广路上)
        {
            把j加入增广路;
            if (j是未盖点 或者 从j的对应项出发有可增广路)
            {
                修改j的对应项为k;
                则从k的对应项出有可增广路,返回true;
            }
        }
    }
    则从k的对应项出没有可增广路,返回false;
}

void 匈牙利hungary()
{
    for i->1 to n
    {
        if (则从i的对应项出有可增广路)
            匹配数++;
    }
    输出 匹配数;
}

为什么这个递归就是在寻找最短路？因为在递归过程中寻找到已经匹配的点会对这个点再进行递归直到到达未盖点，这就构成了一条增广路，具体见算法演示。

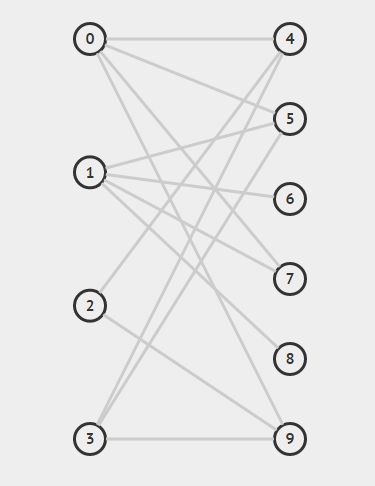
（2）算法演示

看这个图：

算法的演示过程如下：

看这个gif不好看的话可以看看下面这三位的博客。

1. 匈牙利算法 - BYVoid

2. 用于二分图匹配的匈牙利算法 | Comzyh的博客

3. 趣写算法系列之--匈牙利算法，这个很有趣。

(3)算法复杂度

如果二分图的左半边一共有n个点，最多找n条增广路径，如果图中有m条边，每一条增广路径把所有边遍历一遍，所以时间复杂度为O（n*m）。

【算法应用---POJ 1325】

图论中独立和覆盖的关系：
α1 ＋ β1 ＝ n，即：边覆盖数 +边独立数 = n

α0 ＋ β0 ＝ n，即：点覆盖数 +点独立数 = n 

二部图的点覆盖数α0 ＝匹配数β1

二部图的点独立数β0 =边覆盖数α1

上面的这几条关系非常重要，通常其他的问题可以通过这些关系转化成求二分图最大匹配的问题。

题目：POJ 1325

题意：假设有2台机器，A和B。机器A有n种工作模式，分别称为mode_0, mode_1, …, mode_n-1。同样机器B 有m 种工作模式，分别为mode_0, mode_1, … , mode_m-1。刚开始时，A 和B 都工作在模式mode_0。

给定k 个作业，每个作业可以工作在任何一个机器的特定模式下。很显然的是，为了完成所有的作业，必须时不时切换机器的工作模式，但不幸的是，机器工作模式的切换只能通过手动重启机器完成。要求改变作业的顺序，给每个作业分配适的机器，使得重启机器的次数最少。

题解：将两台机器的每个模式看成一个点，则在在每个作业在两台机器上的不同模式之间连一条边。则此题可以看成求最小点覆盖即，求最少的工作模式完成所有作业。在二分图中，最小点覆盖数=匹配数（最大点独立数）。

代码：

#include
#include
#include
#include
#include
using namespace std;
int n,m,k;
const int MAX=100+10;
int g[MAX][MAX];
int vis[MAX];
int match[MAX];

bool dfs(int u)
{
	for(int v=0;v