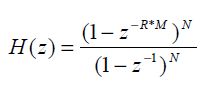数字信号处理学习:基于CIC滤波器的正交检波
基于CIC滤波器的正交检波
Abstract:
本文主要介绍一种基于CIC滤波器的正交检波结构,前部分主要介绍CIC滤波器的实现,并结合MATLAB进行图文分析;后半部分简单介绍正交检波的一些个人理解。
Keywords:
CIC滤波器、抽取、混叠、FFT、欠采样
CIC滤波器初步介绍
Xilinx的FPGA的DSP IP中有一个模块就是CIC滤波器,这个模块可以不用乘法器资源(硬件资源消耗少)来实现低通滤波、内插、抽取:在作为低通滤波器使用时,因为没有用乘法器,所以FPGA内部的delay就可以降到最低,以实现更大的数据吞吐率。同时基于CIC滤波器可以较好地实现数据抽取,已达到降采样率的目的(相同的滤波器特性情况下,降低采样率可以进一步的减少FIR滤波器的阶数,也就能够进一步的减少FPGA的资源使用)。结合这两个特点,CIC滤波器很适合放置在高采样率的ADC的后面,1实现初步滤波,2利用抽取降低采样率,使得后级更加陡峭的滤波器更加容易应用。下面是CIC滤波器的Z域传函:
Figure1
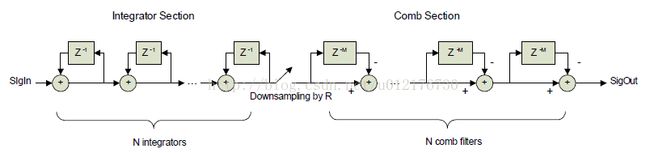
下面是CIC的实现方式:
Figure2
左边是积分部分,共N级,时钟域为降采前(假设R为2)的时钟,如果前级连接一个10MHz的ADC,那么Integrator部分的计算时钟就是10MHz。右边部分是Comb部分,共N级,每一级有M个延时单元,时钟域是降采后的时钟,接上面的例子,就是5MHz。
CIC滤波器仿真
下面给出基于MATLAB的源代码:
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function yn = CIC_Simulat(R,M,N,xn )
yn = zeros(1,fix(length(xn)/R));
IntegratorBuffer = zeros(1,N);
IntegratorIn = 0;
IntegratorOut = 0;
CombBuffer = zeros(N,M);
CombIn = 0;
CombOut = 0;
for i_Sample = 1 : length(xn)
IntegratorIn =xn(i_Sample);
%without delay, get IntegratorOutput at first
%then update the IntegratorBuffer
fori_Integrator = 1 : N
IntegratorOut = IntegratorIn + IntegratorBuffer(i_Integrator);
IntegratorBuffer(i_Integrator) = IntegratorOut;
IntegratorIn = IntegratorOut;
end
%case downsampling, input data to comb from every R IntegratorOutput
ifrem(i_Sample,R) == 0
CombIn= IntegratorOut; % CombIn is Nth Comb's input sigal
fori_Comb = 1 : N
CombOut= CombIn - CombBuffer(i_Comb,end); % CombOut is Nth Comb'soutput sigal
%thenupdate the Nth Comb's CombBuffer
CombBuffer(i_Comb,2:end) = CombBuffer(i_Comb,1:end-1);
CombBuffer(i_Comb,1) = CombIn;
CombIn= CombOut;% reset CombIn as next N+1th Comb's input
end %end for
%at last we get output
yn(fix(i_Sample/R)) = R * CombOut/((R*M)^(N));
end%end if
end%end for
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
基于上面的脚本,来简单的做个实验:
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 该脚本主要用来展示,L和N对FFT的影响
% L越长,也就是实际用来做FFT的采样数据点数越多,那么加窗效应就会减弱,主瓣的宽度就会越小,功率泄露就会减弱(这里特指矩形窗)
% N越长,就是在实际L的基础上,添加的0采样点的个数越多,就会提高频谱的分辨率,也就是最小能够分辨的频率
fftN = 1024; % fft number
sF = 100; %sample frequence
sL = 256; %sample Length
xF1 = 1; %x(n) frequence 1
xF2 = 37; %x(n) frequence 2
xA1 = 1;
xA2 = 1;
xn = xA1 * sin(2*xF1*pi*(0:(1/sF):((sL-1)/sF)))+...
xA2 *sin(2*xF2*pi*(0:(1/sF):((sL-1)/sF)));%Sample freq = sF, length = sL
xF = fft(xn,fftN);
figure
subplot(2,4,1);
plot((((-fftN/2):(fftN/2-1))/fftN)*sF,abs(fftshift(xF)));
xlabel('Normalized frequency') ;
ylabel('Amplitude') ;
title('Input Signal(FFT)');
subplot(2,4,5);
plot((((-fftN/2):(fftN/2-1))/fftN)*sF,abs(fftshift(xF)));
xlabel('Normalized frequency') ;
ylabel('Amplitude') ;
title('Input Signal(FFT)');
%-----------------------Average-----------------------------%
h1L = 10; %h(n) Length
h1n = ones(1,h1L); %get h1(n)
subplot(2,4,2);
plot(h1n,'Ro');
xlabel('Time') ;
ylabel('Amplitude') ;
title('Impulse Response of Average');
h1F = fft(h1n,fftN)/h1L;
subplot(2,4,3);
plot((((-fftN/2):(fftN/2-1))/fftN)*sF,abs(fftshift(h1F)));
xlabel('Normalized frequency') ;
ylabel('Amplitude') ;
title('Magnitude Response Of Moving Average N=10 (FFT)');
y1n = conv(xn,h1n)/h1L;%get y1n
y1F = fft(y1n,fftN);
subplot(2,4,4);
plot((((-fftN/2):(fftN/2-1))/fftN)*sF,abs(fftshift(y1F)));
xlabel('Normalized frequency') ;
ylabel('Amplitude') ;
title('Output Signal Of Moving Average Filter (FFT)');
%------------------------------------------------------------%
%-----------------------CIC-----------------------------%
% Implementing Cascaded Integrator Comb filter with the
% integrator section following the comb stage
% 用R、M、N来控制CIC滤波器的行为,其中
% 实际上RMN都会影响到带宽,最先确定的一般是R,就可以通过设置MN来实现CIC滤波器的幅度响应
% R来控制Downsampling,也即是下采的比例,一般固定不变(会影响衰减的幅度和旁瓣的宽度)
% M来控制带宽,(会影响衰减的幅度和旁瓣的宽度)
% N来控制CIC滤波器的阶数,主要用来控制衰减的的幅度
R = 1;
M = 10;
N = 1;
%理论CIC的冲激响应,冲激响应FFT,信号输出FFT
%理论CIC的冲激响应
z=tf('z');
h3Theory = ((1-z^(-M*R))/(1-z^(-1)))^N;
h3nTheory = impulse(h3Theory)/((R*M)^(N));
%h3nTheory = step(h3Theory);
%实际CIC的冲激响应
DeltaXn = [1 zeros(1,length(h3nTheory)-1)];
%DeltaXn = ones(1,length(h3nTheory));
h3nReal = CIC_Simulat(R,M,N,DeltaXn);
subplot(2,4,6);
hold on;
plot(h3nTheory,'G*');
plot([R:R:R*length(h3nReal)],h3nReal,'R.');
xlabel('Time') ;
ylabel('Amplitude') ;
title('Impulse Response of CIC');
hold off;
%理论CIC的冲激响应的FFT
h3TheoryF = fft(h3nTheory,fftN);
%实际CIC的冲激响应的FFT
h3RealF = fft(h3nReal,fftN);
subplot(2,4,7);
hold on;
plot((((-fftN/2):(fftN/2-1))/fftN)*sF,abs(fftshift(h3TheoryF)),'G-');
plot((((-fftN/2):(fftN/2-1))/fftN)*(sF/R),abs(fftshift(h3RealF)),'R-');
xlabel('Normalized frequency') ;
ylabel('Amplitude') ;
title(' Magnitude Response Of CIC (FFT)');
hold off;
y3n=CIC_Simulat(R,M,N,xn);
y3F = fft(y3n,fftN);
subplot(2,4,8);
plot((((-fftN/2):(fftN/2-1))/fftN)*(sF/R),abs(fftshift(y3F)));
xlabel('Normalized frequency') ;
ylabel('Amplitude') ;
title('Output Signal Of CIC Filter (FFT)');
%------------------------------------------------------------%
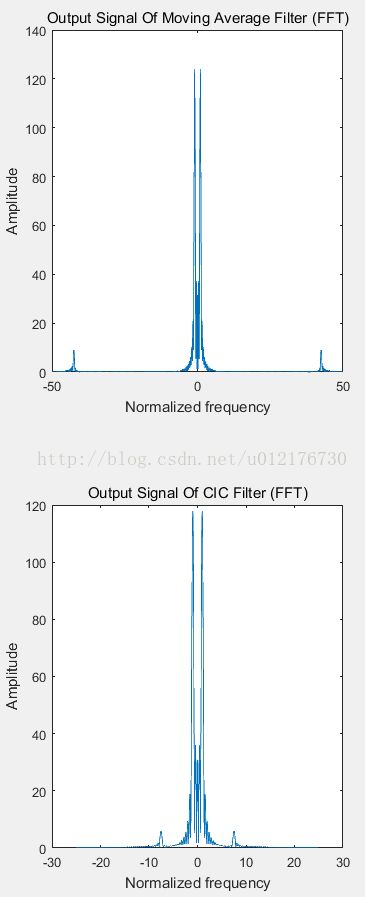
上面的代码主要是做了一个对比实验,因为当R=1,N=1,M=10时,CIC滤波器就是实现了移动平均滤波器。将CIC滤波器以及移动平均滤波器的冲激响应和冲激响应的FFT进行对比,结果如下图所示:
Figure 3 移动平均滤波器:输入信号的频谱、冲激响应、冲激响应幅频曲线、滤波后的输出信号的频谱
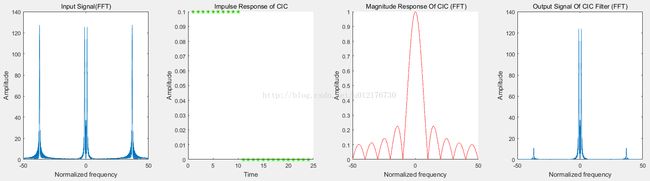
Figure 4 CIC滤波器(R=1、M=10、N=1):输入信号的频谱、冲激响应、冲激响应幅频曲线、滤波后的输出信号的频谱
经过对比,两者确实具备相同的冲激响应和幅频特性,结果输出信号自然是一样。
现将R=2,M=10,N=2,,得到下图:
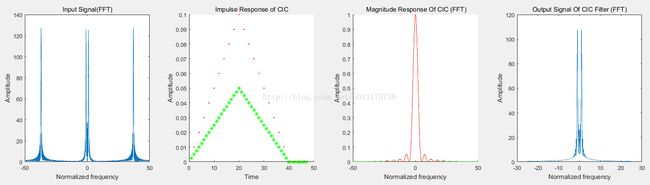
Figure 5 CIC滤波器(R=2、M=10、N=2):输入信号的频谱、冲激响应、冲激响应幅频曲线、滤波后的输出信号的频谱
特别需要注意的是上图左2,红色点和绿色点没有重合,同时绿色点数量也是红色点的2倍。这是因为R=2,这里有一个降采样率(抽取)的过程,那自然冲激响应的有效点数也是原来的一半,幅度却是两倍(红线是CIC抽取的响应,绿点是没有降采的响应)。再看右2图,因为抽取的原因,红线的频率范围只有绿线的1半,但是频率重合部分的幅频响应是一致的。所以说同样的传函形式:
可以用降采(抽取)的算法实现(红线),也可以不降采(绿线)来实现,最终幅频响应是一样的。
再回过头对比figure1和figure3,可以明显的看到,高阶CIC高频部分衰减还是可以接受的。但是CIC抽取滤波器存在两个问题:
1. 抽取时会发生频谱折叠(或说频谱复制),有可能会发生混叠;
做如下修改:
xF2 = 42.5; %x(n) frequence 2
R =2;
M =10;
N =1;
此时两个滤波器的实际输出如下:
Figure7
可以看到,原来的频率应该是1Hz和42.5Hz,但是CIC滤波器后变成了1Hz和7.5Hz,这是因为在降采后发生了频率复制(折叠),那原来在42.5Hz的频率向左移动50Hz(降采后的采样率)-7.5Hz,同理-42.5Hz移动到了7.5Hz。这就是混频,一般发生在欠采样(抽取后采样率不够大)的情况下!
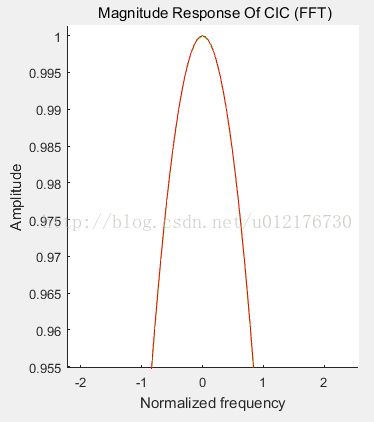
2. 带通部分平整度不够;
Figure8 CIC通带部分展开后,却是不够平整
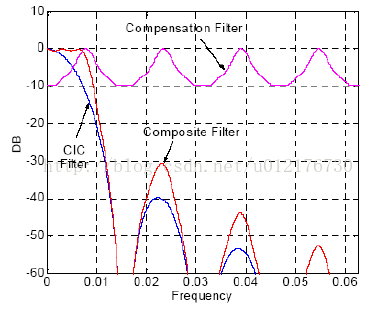
前者可以通过适当选取采样频率进行规避,后者可以在CIC滤波器后面接一个补偿器,将通带部分的幅频响应变得更加平整,如下图所示:
Figure9 经过补偿的CIC滤波器,见Xilinx的技术手册-pg140
小结:
上面主要介绍了CIC滤波器的特点,接下来介绍下应用。
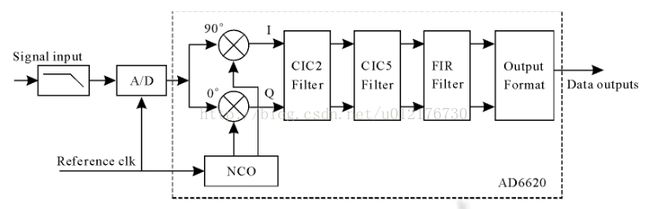
正交检波介绍:
Figure10 图片来自《用于低场磁共振成像的直接射频采样数字接收机》
具体的理论可以看信号与系统等书籍,这里先给出MATLAB的仿真代码:
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
R = 2;
M = 10;
N = 1;
sN = 5120; %sample number per fft
fftN = 10240; %fft number
sF1M = 1e6; %sample qrequence
sF5M = 5e6; %sample qrequence
fc = 1.11e6;
%R=2,N=1,M=10测试环境
%混频1 载波中频 1.4625e6(fc-fs<0.5fs) :左上图两根蓝线就是用5M去采样获得的FFT,红线就是用1M去采样获得的FFT,
%右边的红线0.4625就是右边的蓝线1.4625频移1M(fs)得到,左边的红线-0.4625是由左边的蓝线-1.4625频移1M得到
%实际上在左边的红线的左边,还有一根很被隐藏了的红线-0.5375,以及右边有一根红线0.5375。因为不落在±0.5之内
%但是在用NCO进行频谱搬移后,会发现这根线-0.5375的线移动到±0.075处,也就是移动到了实际有效带宽范围,如左下图所示
%这个时候看右下图的检波信号,会发现有大量的高频谐波在上面,正是这个原因!1.5>fc>1.375会有这个问题
%混频2
%载波中频为1.25和1.375之间时,虽然上述干扰谱线在经过NCO移频后已经在±0.5之外了,但是如果R大于等于2,就会有进一步频谱幅值
%但是一般这时的干扰谱线已经经过充分的滤波,所以即使混叠了,影响也不大!
%实际上都需要结合中频带宽,中频中心频率,采样频率,降采样率共同来看是否有混叠
fa = [0.0022e6 0.0032e6 0.0042e6 0.0052e6];
fp = 0.0013e6;
fnco =rem(fc,sF1M);
t1M=0:1/sF1M:(sN-1)/sF1M;
t5M=0:1/sF5M:(sN-1)/sF5M;
an1M =cos(2*pi*fa(1)*t1M)+sin(2*pi*fa(2)*t1M)+cos(2*pi*fa(3)*t1M)+sin(2*pi*fa(4)*t1M);
an5M =cos(2*pi*fa(1)*t5M)+sin(2*pi*fa(2)*t5M)+cos(2*pi*fa(3)*t5M)+sin(2*pi*fa(4)*t5M);
pn1M = pi*cos(2*pi*fp*t1M);
pn5M = pi*cos(2*pi*fp*t5M);
xn1M = an1M .* sin(2*pi*fc*t1M + pn1M);
xn5M = an5M .* sin(2*pi*fc*t5M + pn5M);
x1MF = fft(xn1M,fftN)/sN;
x5MF = fft(xn5M,fftN)/sN;
ncoI1M = cos(2*pi*fnco*t1M);
ncoQ1M = sin(2*pi*fnco*t1M);
ncoI1MF = fft(ncoI1M,fftN)/sN;
ncoQ1MF = fft(ncoQ1M,fftN)/sN;
sIn1M = xn1M .* ncoI1M;
sQn1M = xn1M .* ncoQ1M;
sIn1MF = fft(sIn1M,fftN)/sN;
sQn1MF = fft(sQn1M,fftN)/sN;
sIcic1RM = CIC_Simulat(R,M,N,sIn1M);
sQcic1RM = CIC_Simulat(R,M,N,sQn1M);
sIcic1RMF = fft(sIcic1RM,fftN)/sN;
sQcic1RMF = fft(sQcic1RM,fftN)/sN;
sn = sIcic1RM + i * sQcic1RM;
sMag = abs(sn);
%理论CIC的冲激响应
z=tf('z');
h3Theory = ((1-z^(-M*R))/(1-z^(-1)))^N;
h3nTheory = impulse(h3Theory)/((R*M)^(N));
%实际CIC的冲激响应
DeltaXn = [1 zeros(1,length(h3nTheory)-1)];
%DeltaXn = ones(1,length(h3nTheory));
hnReal = CIC_Simulat(R,M,N,DeltaXn);
hRealF = fft(hnReal,fftN);
subplot(2,2,1);
hold on;
plot((((-fftN/2):(fftN/2-1))/fftN)*(sF1M),abs(fftshift(x1MF)),'R-');
plot((((-fftN/2):(fftN/2-1))/fftN)*(sF5M),abs(fftshift(x5MF)),'B--');
xlabel('Frequence') ;
ylabel('Amplitude') ;
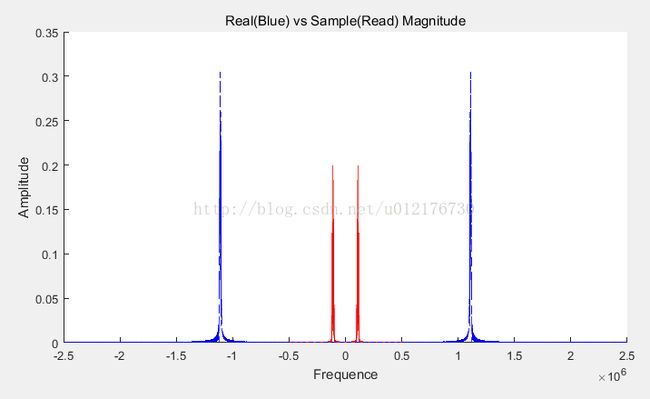
title('Real(Blue) vs Sample(Read) Magnitude');
hold off;
subplot(2,2,2)
hold on;
plot((((-fftN/2):(fftN/2-1))/fftN)*(sF1M),abs(fftshift(x1MF)),'R--');
plot((((-fftN/2):(fftN/2-1))/fftN)*(sF1M),abs(fftshift(ncoI1MF)),'G--');
plot((((-fftN/2):(fftN/2-1))/fftN)*(sF1M),abs(fftshift(sIn1MF)),'B--');
plot((((-fftN/2):(fftN/2-1))/fftN)*(sF1M/R),abs(fftshift(sIcic1RMF)),'k-');
plot((((-fftN/2):(fftN/2-1))/fftN)*(sF1M/R),abs(fftshift(hRealF)),'y-');
xlabel('Frequence') ;
ylabel('Amplitude') ;
title('Sample(Red) vs NCOI(Green) vs SI(Blue) vsSICIC(Black)Magnitude');
hold off;
subplot(2,2,3)
hold on;
plot((((-fftN/2):(fftN/2-1))/fftN)*(sF1M),abs(fftshift(x1MF)),'R--');
plot((((-fftN/2):(fftN/2-1))/fftN)*(sF1M), abs(fftshift(ncoQ1MF)),'G--');
plot((((-fftN/2):(fftN/2-1))/fftN)*(sF1M),abs(fftshift(sQn1MF)),'B--');
plot((((-fftN/2):(fftN/2-1))/fftN)*(sF1M/R),abs(fftshift(sQcic1RMF)),'k-');
plot((((-fftN/2):(fftN/2-1))/fftN)*(sF1M/R),abs(fftshift(hRealF)),'y-');
xlabel('Frequence') ;
ylabel('Amplitude') ;
title('Sample(Red) vs NCOQ(Green) vs SQ(Blue) vsSQCIC(Black) Magnitude');
hold off;
subplot(2,2,4)
hold on;
plot(((0:(sN-1))/sF1M),xn1M,'R-');
plot(((0:(sN-1))/sF5M),xn5M,'G-');
plot(((0:((sN/R)-1))/(sF1M/R)),sMag,'k--');
xlabel('Sample Time') ;
ylabel('Amplitude') ;
title('Real(Green) vs Sample(Red) vs |S|(Black)Magnitude');
hold off;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
将载波(中频)fc设置为1.11e6,这个时候我们用两种采样率去采集这个波形,得到的图案是:
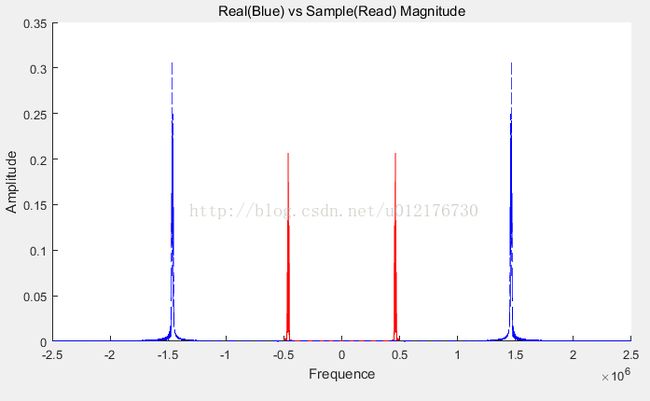
Figure11 红线是1M采样率采样后所做的FFT,蓝线是5M采样率的FFT
可以看到,用5MHz进行采样时能够获得正确的频谱,而用1MHz进行采样时,获得的就是经过复制后的频谱,其中原来蓝线1.11M处的跑到了0.11M(红线),而原来蓝线-1.11M的跑到了-0.11M。这是一个典型的欠采样,也就是用低采样率去采集中频信号,然后利用频谱的复制,得到可操作的频谱。
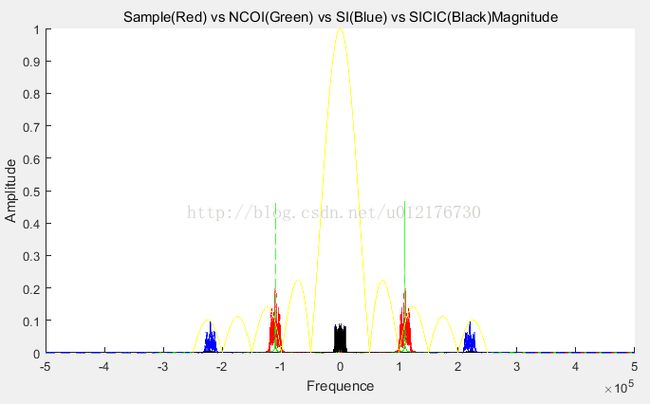
这时再用NCO生成一个余弦和正弦分别乘以ADC后的数据,可以得到如下SI和SQ频谱:
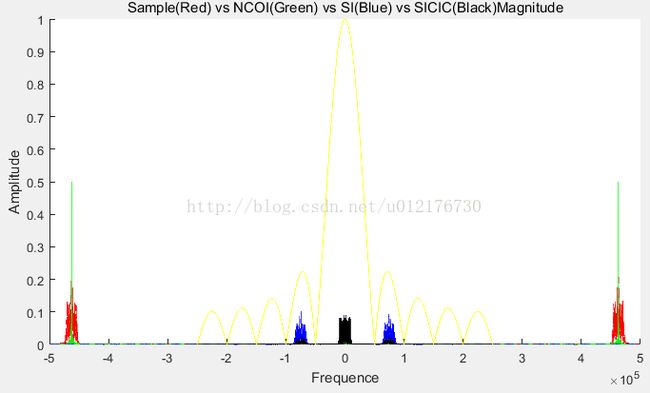
Figure12 SI:将ADC的数据(红)乘以余弦(绿)得到SI(蓝),同时经过CIC滤波器(幅频特性黄线)后变成SICIC(黑)
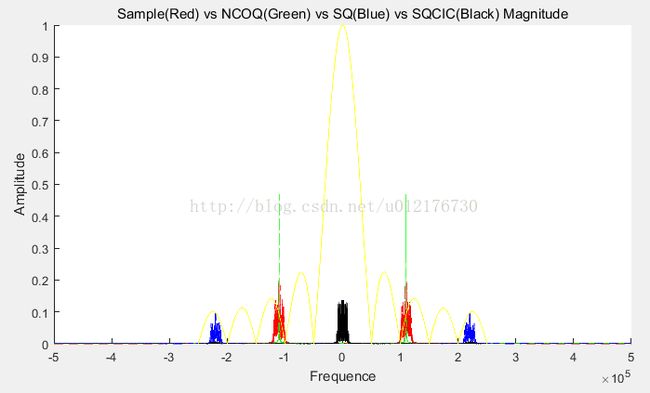
Figure13 将ADC的数据(红)乘以余弦(绿)得到SQ(蓝),同时经过CIC滤波器(幅频特性黄线)后变成SQCIC(黑)
通过上面两张图,可以看到ADC乘以NCO信号后,将红线分别挪到了蓝线处,其中一处蓝线在2.2M,另一处在0M(蓝线被黑线覆盖了)。然后经过CIC滤波器后进行滤波,将2.2M处的高次谐波滤掉,就得到了干净的SICIC或者SQCIC。
将SQCIC和SICIC的合并:
sn = sIcic1RM + i * sQcic1RM;
sMag = abs(sn);
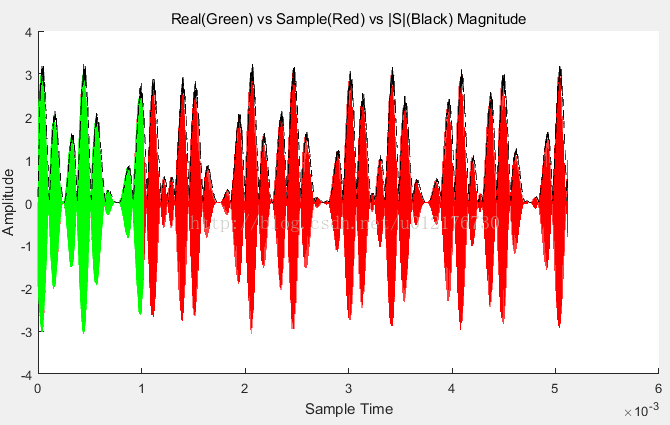
最终得到了检波信号的时间域信息,如下图:
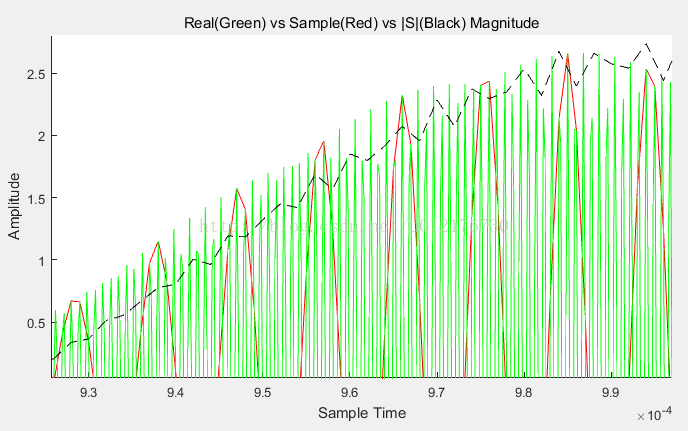
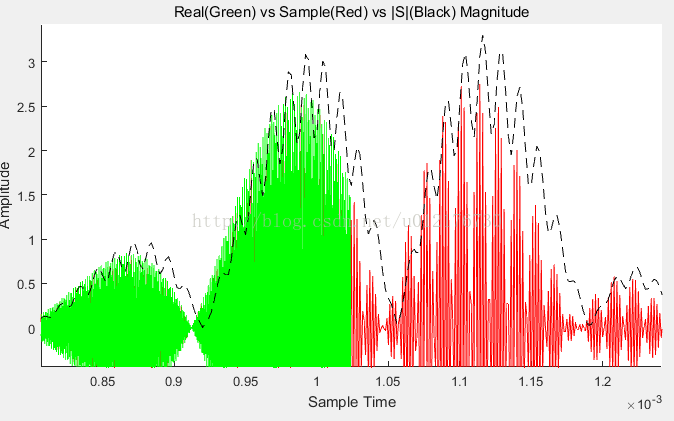
Figure 14 绿线是5M采样,红线是1M采样,黑色虚线是检波信号(代表包络,有延时)
Figure 15 放大后:绿线是5M采样,红线是1M采样,黑色虚线是检波信号(代表包络,有延时)
可以看到这种方式确实可以实现检波;
接下来分析一下特殊情况:
%R=2,N=1,M=10测试环境
混频1 载波中频 1.4625e6(fc-fs<0.5fs) :左上图两根蓝线就是用5M去采样获得的FFT,红线就是用1M去采样获得的FFT,右边的红线0.4625就是右边的蓝线1.4625频移1M(fs)得到,左边的红线-0.4625是由左边的蓝线-1.4625频移1M得到实际上在左边的红线的左边,还有一根很被隐藏了的红线-0.5375,以及右边有一根红线0.5375。因为不落在±0.5之内但是在用NCO进行频谱搬移后,会发现这根线-0.5375的线移动到±0.075处,也就是移动到了实际有效带宽范围,如左下图所示。这个时候看右下图的检波信号,会发现有大量的高频谐波在上面,正是这个原因!1.5>fc>1.375会有这个问题。
Figure16 这个图看不出异常
Figure17 问题来了
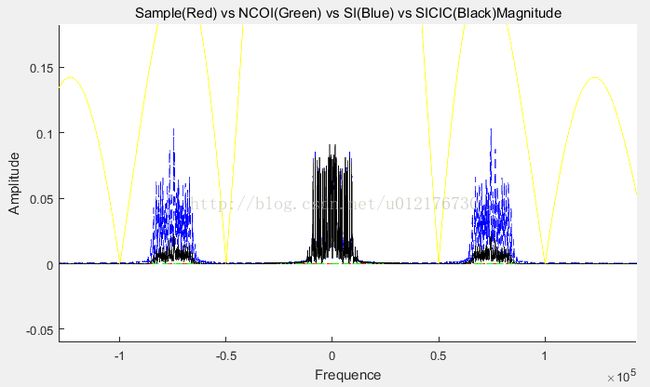
Figure 18 放大了,发现有谐波混叠进来了,而且恰好落在了旁瓣里,没有滤干净
下图可以看到,检波信号里面确实混杂了很多高频谐波
Figure 19