DOG角点检测——opencv实现

1.原理

Difference of Gaussian(DOG)是高斯函数的差分。将两幅图像在不同参数下的高斯滤波结果相减，得到DoG图。步骤：

• 处理一幅图像在不同高斯参数下的DoG
  用两个不同的5x5高斯核对图像进行卷积，然后再相减的操作。重复三次得到三个差分图A,B,C。

• 根据DoG求角点
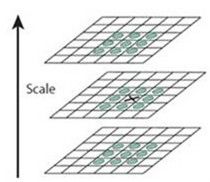
  计算出的A,B,C三个DOG图中求图B中是极值的点。图B的点在当前由A,B,C共27个点组成的block中是否为极大值或者极小值。若满足此条件则认为是角点。
  

  

2.实现细节

2.1 差分得到DoG图

Mat Process(Mat &img, double sig1, double sig2, Size Ksize)

• converTo()
  直接读取灰度图会得到CV_8UC1类型的mat，是单通道uchar型矩阵，因此高斯滤波后相减都是整型非负数据，影响后面进行比较取极值的步骤。所以需要将原本的数据类型转化为CV_32FC1即单通道float型数据。再进行后续的操作
• subtract()
  两个mat类型相减直接用这个就好了。刚开始查到cvSub函数是老版本的，里面的指针乱七八糟的都挺复杂的，后在官方说明上找到这个c++版本的函数。现在的操作基本都是这个了。

2.2 求取当前block极值得到角点

Mat getExtrema(Mat &A, Mat &B, Mat &C, int thresh){}
    block.release();
    block.push_back(A(Range(i - 1, i + 2), Range(j - 1, j + 2)));
    block.push_back(B(Range(i - 1, i + 2), Range(j - 1, j + 2)));
    block.push_back(C(Range(i - 1, i + 2), Range(j - 1, j + 2)));
    minMaxLoc(block, &minv, &maxv, &minLoc, &maxLoc);

取出A，B，C中3x3的小块存放在一个mat里，然后利用自带的求取最大最小值函数minMaxLoc得到最大最小值和其位置。然后判断该点 (i,j) 是否为极值点。每个循环刷新释放block。

2.3 求取当前block极值得到角点

void drawExtrema(Mat &imgB, Mat &extr)

将得到的极值点在原图像中显示。由于imread(img,0)得到的是单通道灰度图 ，opencv提供的cirle()和line()函数在img上无法显示，所以用imread(imgB)得到一个三通道的灰度图，然后在这个imgB上画出标记点。

2.4 讨论

用样例测试图600x1200像素点的时候，运算速度很慢，逐步运行发现时间主要消耗在getExtrema()函数上。原因可能是：

• mat.push_back()截取矩阵然后合并得到新矩阵用这个操作比较费时间。如果改进的话可以直接用一个数组，将三个3x3矩阵的数据直接放进去。
• minMaxLoc()求取当前矩阵最大最小值和响应位置。这个函数涉及到排序可能也费时间。因为只用判断当前 (i,j) 点是否是极值，其实可以将这27个数据直接减去mat.at(i,j)根据是否都大于或者小于零来判断极值。

然而我已经懒得改了……需要优化速度的话再动手。

3.测试结果

输入图像：

输出结果：

参考

1. DoG (Difference of Gaussian)角点检测
2. 斑点检测
3. 将mat数据输出到文件

查了很多东西最后都查到opencv的官方文档去了。调试时用到了参考链接3。

5.代码

#include 
#include 
#include "opencv2/core/core.hpp"  
#include "highgui.h"  
#include "opencv2/imgproc/imgproc.hpp"  

using namespace cv;
using namespace std;
Mat Process(Mat &A, double sig1, double sig2, Size Ksize)
{
    Mat AF, out, out1, out2;
    A.convertTo(AF, CV_32FC1);
    GaussianBlur(AF, out1, Ksize, sig1, 0);
    GaussianBlur(AF, out2, Ksize, sig2, 0);
    subtract(out1, out2, out);
    return out;
}

Mat getExtrema(Mat &A, Mat &B, Mat &C, int thresh)
{
    Mat block;
    Mat extr = Mat::zeros(A.rows, A.cols, CV_32FC1);
    double minv, maxv;
    Point minLoc, maxLoc;
    for (int i = 1; i < A.rows - 2; i++)
    {
        for (int j = 1; j < A.cols - 2; j++)
        {
            block.release();
            block.push_back(A(Range(i - 1, i + 2), Range(j - 1, j + 2)));
            block.push_back(B(Range(i - 1, i + 2), Range(j - 1, j + 2)));
            block.push_back(C(Range(i - 1, i + 2), Range(j - 1, j + 2)));
            minMaxLoc(block, &minv, &maxv, &minLoc, &maxLoc);
            if ((maxLoc.x == 1 && maxLoc.y == 4) && maxv >(double)thresh)
                extr.at<float>(i, j) = 1;
            if ((minLoc.x == 1 && minLoc.y == 4) && minv < (double)(-thresh))
                extr.at<float>(i, j) = -1;
        }
    }
    return extr;
}

void drawExtrema(Mat &img, Mat &extr)
{
    Point center;
    int r = 2;
    for (int i = 0; i < img.rows; i++)
    {
        for (int j = 0; j < img.cols; j++)
        {
            if (extr.at<float>(i, j) == -1)
            {
                center = Point(j, i);
                circle(img, center, r, Scalar(0, 255, 0));
            }
            if (extr.at<float>(i, j) == 1)
            {
                center = Point(j, i);
                circle(img, center, r, Scalar(0, 0, 255));
            }
        }
    }

    namedWindow("DoG");
    imshow("DoG", img);
    waitKey(0);
}

int main(int argc, char** argv)
{
    char file_name[] = "result1.png";
    Mat img = imread(file_name, 0);
    Mat A, B, C, a;
    int threshold = 3;
    A = Process(img, 0.3, 0.4, Size(5, 5));
    B = Process(img, 0.6, 0.7, Size(5, 5));
    C = Process(img, 0.7, 0.8, Size(5, 5));
    a = getExtrema(A, B, C, threshold);
    //const char* filename = "output.txt";
    //writeMatToFile(B, filename);
    Mat imgB = imread(file_name);
    drawExtrema(imgB, a);
    return 0;
}