含有隐函数的离散常微分方程求解

　　前段时间代码中碰到一个含有隐函数的离散常微分方程的求解问题，在这里和大家讨论一下其求解方法。
　　首先，介绍一下什么是常微分方程。微分方程求解问题在大学高等数学中学过，当我碰到这个问题后，我还专门去翻了一下高数的书（都还给老师了ORZ）。微分方程的定义是：凡含有参数，未知函数和未知函数导数 (或微分) 的方程，称为微分方程。而常微分方程是指未知函数是一元函数的微分方程。
　　下面是一个简单的常微分方程：
　　
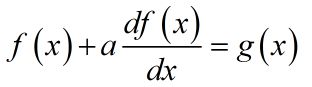
　　上式中，f(x)和g(x)都是x的显式函数，a是常数，解上边的微分方程可以得到f(x)的函数表达式。对于连续的情况，即：f(x)和g(x)都是连续函数，我们在大一大二学的微积分或者高数书上都有详细的求解方法。例如：可采用常数变易法，通过常数变易法，可求出一阶线性微分方程的通解。带入初值即可求出其特解。
　　常徽分方程是研究自然科学社会科学中的事物运动和变化规律的最基本的数学理论及方法自然界中很多事物的运动规律，如牛顿运动定律，万有引力定律等， 社会科学中很多现象的演变规律如人口发展规律市场均衡价格的变化等 都可用常徽分方程来描述。但是我们在工程中遇到的常微分方程往往不是我们学过的理想形式，下边就分析我遇到的一种情况：
　　g(x)是采集的离散值，不知道函数形式，是一个隐函数，总结一下就是：g(x)是隐函数的离散形式的常微分方程求解。对于这个问题，我认为可以用前向欧拉、函数拟合或者构造优化求解模型，利用优化方法进行求解。我这里介绍利用欧拉法和函数拟合的方法求解这个常微分方程。

1.利用欧拉法求解含有隐函数的微分方程

　　这个方法思路非常简单，就是利用差分方程代替微分方程。得到f(x)的每个采样点的值。
　　
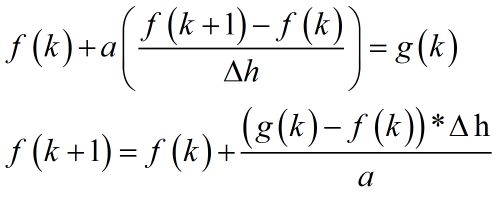
　　通过上式我们可以得到f(x)在每个点的值。在程序数据处理中，我们得到f(x)的所有值就足够了。下边我用matlab对此方法进行了仿真：

%% ********用欧拉的方式求解ode *******%%
%%
clc;
clear all;
close all;
%% 定义构造函数参量
func1 = @(x)sin(2*pi*x)+cos(2*pi*x);   
func2 = @(x)3*x+1;
func3 = @(x)x.*x+1;
f1_init = func1(0);           %设置初始点
f2_init = func2(0);
f3_init = func3(0);
constant_A = 2;               %微分方程常系数
sampling_step = 0.01;         %采样间隔
% sampling_step = 1;          %采样间隔
% samp_max = 100;
samp_max = 10;
samp_min = 0;
samp_num = (samp_max-samp_min)/sampling_step;
sampling_x = linspace(samp_min,samp_max,samp_num);
%% 通过构造函数获得恒解空间
% func1_diff = diff(func1,'x');
% func2_diff = diff(func2,'x');
% func3_diff = diff(func3,'x');
func1_diff = @(x)2*pi*cos(2*pi*x)-2*pi*sin(2*pi*x);
func2_diff = @(x)3;
func3_diff = @(x)2*x;
for i=1:samp_num
    g1_fun(i) = func1(sampling_x(i))+constant_A*func1_diff(sampling_x(i));
    g2_fun(i) = func2(sampling_x(i))+constant_A*func2_diff(sampling_x(i));
    g3_fun(i) = func3(sampling_x(i))+constant_A*func3_diff(sampling_x(i));
end
% 通过构造的反解
func1_Inverse = [f1_init];
func2_Inverse = [f2_init];
func3_Inverse = [f3_init];
for k=1:samp_num-1
    func1_Inverse(k+1) = func1_Inverse(k)+(g1_fun(k)-func1_Inverse(k))*sampling_step/constant_A;
    func2_Inverse(k+1) = func2_Inverse(k)+(g2_fun(k)-func2_Inverse(k))*sampling_step/constant_A;
    func3_Inverse(k+1) = func3_Inverse(k)+(g3_fun(k)-func3_Inverse(k))*sampling_step/constant_A;
end
%% 画图比较
raw_fun1_data = func1(sampling_x);   %准确数字
raw_fun2_data = func2(sampling_x);   %线性可以完全拟合
raw_fun3_data = func3(sampling_x);
figure;
plot(sampling_x,raw_fun1_data,'r');
hold on;
plot(sampling_x,func1_Inverse,'b');
figure;
plot(sampling_x,raw_fun2_data,'r.');
hold on;
plot(sampling_x,func2_Inverse,'b.');
figure;
plot(sampling_x,raw_fun3_data,'r.');
hold on;
plot(sampling_x,func3_Inverse,'b.');

　　我测试了正余弦、线性和二次函数，都能很好地完成工作。下边是正余弦函数的测试结果：

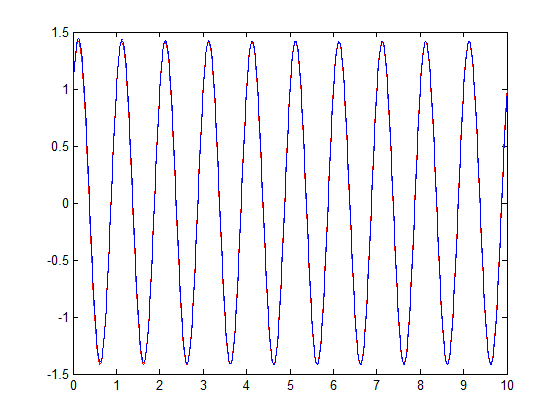
2.利用函数拟合方式求解含有隐函数的微分方程

　　由于函数g(x)是离散的隐函数，所以很容易想到可以用函数拟合的方法去得到g(x)的函数形式。我采用了多项式拟合的方法去拟合g(x)。方便地是，matlab提供了函数拟合和求解ode（微分方程）的函数。下边给出代码：

%% ********用函数拟合的方式求解ode（polyfit()和ode()函数*******%%
%%
clc;
clear all;
close all;
%% 定义构造函数参量
func1 = @(x)sin(2*pi*x)+cos(2*pi*x);   
func2 = @(x)3*x+1;
func3 = @(x)x.*x+1;
f1_init = func1(0);           %设置初始点
f2_init = func2(0);
f3_init = func3(0);
constant_A = 2;               %微分方程常系数
sampling_step = 0.01;         %采样间隔
% sampling_step = 1;          %采样间隔
% samp_max = 100;
samp_max = 10;
samp_min = 0;
samp_num = (samp_max-samp_min)/sampling_step;
sampling_x = linspace(samp_min,samp_max,samp_num);
%% 通过构造函数获得恒解空间
% func1_diff = diff(func1,'x');
% func2_diff = diff(func2,'x');
% func3_diff = diff(func3,'x');
func1_diff = @(x)2*pi*cos(2*pi*x)-2*pi*sin(2*pi*x);
func2_diff = @(x)3;
func3_diff = @(x)2*x;
for i=1:samp_num
    g1_fun(i) = func1(sampling_x(i))+constant_A*func1_diff(sampling_x(i));
    g2_fun(i) = func2(sampling_x(i))+constant_A*func2_diff(sampling_x(i));
    g3_fun(i) = func3(sampling_x(i))+constant_A*func3_diff(sampling_x(i));
end
%% 利用多项式拟合g(x)
g1_fit = polyfit(sampling_x,g1_fun,5);
g2_fit = polyfit(sampling_x,g2_fun,3);
g3_fit = polyfit(sampling_x,g3_fun,3);
g1_func_fit = @(x)g1_fit(1)*x.*x.*x.*x.*x+g1_fit(2)*x.*x.*x.*x+g1_fit(3)*x.*x.*x+g1_fit(4)*x.*x+g1_fit(5)*x+g1_fit(6);
g2_func_fit = @(x)g2_fit(1)*x.*x.*x+g2_fit(2)*x.*x+g2_fit(3)*x+g2_fit(4);
g3_func_fit = @(x)g3_fit(1)*x.*x.*x+g3_fit(2)*x.*x+g3_fit(3)*x+g3_fit(4);
%% ode求解
% odefun1 = @(x,f1)(g1_fit(1)*x.*x.*x+g1_fit(2)*x.*x+g1_fit(3)*x+g1_fit(4)-f1)/constant_A;
odefun1 = @(x,f1)(g1_fit(1)*x.*x.*x.*x.*x+g1_fit(2)*x.*x.*x.*x+g1_fit(3)*x.*x.*x+g1_fit(4)*x.*x+g1_fit(5)*x+g1_fit(6))/constant_A;
odefun2 = @(x,f2)(g2_fit(1)*x.*x.*x+g2_fit(2)*x.*x+g2_fit(3)*x+g2_fit(4)-f2)/constant_A;
odefun3 = @(x,f3)(g3_fit(1)*x.*x.*x+g3_fit(2)*x.*x+g3_fit(3)*x+g3_fit(4)-f3)/constant_A;
f1_init = func1(0.01);           %设置初始点
f2_init = func2(0.01);
f3_init = func3(0.01);
[x,f1] = ode45(odefun1,[0.01:0.01: 10],f1_init);
[x,f2] = ode45(odefun2,[0.01:0.01: 10],f2_init);
[x,f3] = ode45(odefun3,[0.01:0.01: 10],f3_init);
%% 画图比较
sampling_x = [0.01:0.01: 10];
raw_fun1_data = func1(sampling_x);      %准确数字
raw_fun2_data = func2(sampling_x);      %线性可以完全拟合
raw_fun3_data = func3(sampling_x);
figure;
plot(sampling_x,raw_fun1_data,'r');
hold on;
plot(x,f1,'b');
figure;
plot(sampling_x,raw_fun2_data,'r.');
hold on;
plot(x,f2,'b.');
figure;
plot(sampling_x,raw_fun3_data,'r.');
hold on;
plot(x,f3,'b.');

　　我测试了正余弦、线性和二次函数，都能很好地完成工作。结果会发现，线性，二次函数都能很好的用此方法解决，但是无法完成正余弦函数的求解。因为在函数拟合部分，很难用多项式来拟合正余弦函数。
　　具体的实验结果，大家可以用代码跑一下。