机器学习的分类
机器学习的分类
- 监督学习
- 无监督学习
- 半监督学习
- 强化学习
监督学习
在监督学习中,提供给算法的包含所解决方案的训练数据,称为标签或标记
一、目的
利用一组带有标签的数据,学习从输入到输出的映射,然后将这种映射关系应用到未知数据上,达到分类和回归的目的。
分类:
当输出是离散的,学习任务为分类任务。分类模型根据输入的标签数据,训练自己的模型,学习出一个适合这组数据的分类器,当有新的数据(非训练数据)需要进行 类别判断时,就可以将这组新数据作为输入传送给完成学习的分类器进行判断。
回归:
当输出是连续的,学习任务为回归任务。统计学分析数据的方法,目的在于了解两个或多个变量之间的相关性,并建立数学模型以便观察特定变数来预测研究者感兴趣的变数。回归分析可以帮助人们了解自变量变化是因变量的变化量。一般来说,通过回归分析我们可以由给出的自变量估计因变量的条件期望。
二、常用算法
- K-近邻(k-Nearest Nrighbors)
- 线性回归(Linear Regression)
- 逻辑回归(Logistic Regression)
- 支持向量机(Support Vector Machines ,SVM)
- 决策树、随机森林(Decision Trees and Random Forests)
- 神经网络(Neural Networks)
- 朴素贝叶斯(naivebayes)
无监督学习
一、目标
利用无标签的数据学习数据的分布或数据之间的关系。
- 有监督学习和无监督学习最大的区别在于数据是否有标签
- 无监督学习最常应用的场景是聚类和降维
聚类(clustering):
根据数据的“相似性”将数据分为多类的过程。评估两个不同样本之间的“相似性”,通常使用的方法就是技术样本之间的“距离”。使用不同的方法计算样本间的距离会关系到聚类结果的好坏。 - 欧式距离
最常用的一种距离度量方式,源于欧式空间中两点的距离:
d = ∑ k = 1 n ( x 1 k − x 2 k ) 2 d=\sqrt{\sum_{k=1}^n(x_{1k}-x_{2k})^2} d=k=1∑n(x1k−x2k)2
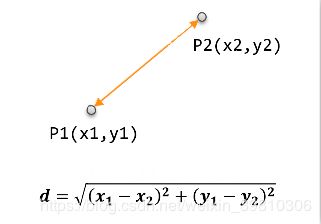
- 曼哈顿距离
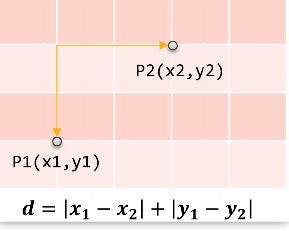
曼哈顿距离也称“城市街区距离”,类似于城市中驾车行驶,从一个十字路口到另外一个十字路口的距离:
d = ∑ k = 1 n ∣ x 1 k − x 2 k ∣ d = \sum_{k=1}^n|x_{1k}-x_{2k}| d=k=1∑n∣x1k−x2k∣
- 马氏距离
表示数据的协方差距离,是一种尺度无关的度量方式。也即是说马氏距离会先将样本点的各个属性标准化,在计算样本间的距离:
d ( x t , y j ) = ( x t − x j ) T s − 1 ( x t − x j ) d(x_t,y_j)=\sqrt{(x_t-x_j)^Ts^{-1}(x_t-x_j)} d(xt,yj)=(xt−xj)Ts−1(xt−xj)

- 夹角余弦
余弦相似度用向量空间中两个向量夹角的余弦值作为衡量两个样本差异的大小。余弦值越接近1,说明两个样本越相似:
c o s ( θ ) = ∑ k = 1 n x 1 k x 2 k ∑ k = 1 n x 1 k 2 ∑ k = 1 n x 2 k 2 cos(\theta)=\frac{\sum_{k=1}^nx_{1k}x_{2k}}{\sqrt{\sum_{k=1}^nx^2_{1k}}\sqrt{\sum_{k=1}^nx^2_{2k}}} cos(θ)=∑k=1nx1k2∑k=1nx2k2∑k=1nx1kx2k

二、常用算法
- 聚类
- k-平均算法(k-Means)
- 分层聚类分析(HCA)
- 最大期望算法
- 可视化、降维
- 主成分分析(PCA)
- 核主成分分析(Kernel PCA)
- 局部线性嵌入(LLE)
- t-分部随机近邻嵌入(t-SEN)
- 关联规制学习
- Apriori
- Eclat
半监督学习
有些算法可以处理部分标记的训练数据——通常是大量未标记的数据和少量的标记数据。
有如:你在手机中存储了大量的照片,手机能够自动识别出人物A出现的哪几张图片中,人物B出现在哪几张图片中,但是他无法分辨人物A是谁,这就需要我们给人物A上标签,他就可以给每张照片中的人物A命名,有利于人物图片搜索。
大多数半监督学习是无监督学习和监督学习的结合。
强化学习
强化学习系统(在其语境中称为智能体)能够观察环境,做出选择,执行操作,并获得回报(reward),或者是以负面回报的形式获得惩罚。他必须自行学习什么是最好的策略(policy),从而随着时间推移获得最大的回报。
-
蒙特卡洛强化学习
在现实的强化学习任务中,环境的转移概率、奖励函数往往很难得知,甚至很难获得环境中有多少状态,蒙特卡洛强化学习为免模型学习,可以不依赖环境建模。采用多次采样,然后求取平均累计奖赏作为期望累计奖赏的近似。 -
Q-Learning算法
^深度强化学习(DRL) -
传统强化学习:真实环境中的状态数目过多,求解困难
-
深度强化学习:将深度学习和强化学习结合在一起,通过深度神经网络直接学习环境(观察)与状态动作值函数QW(s,a)之间的映射关系,简化问题的求解。