最优化方法 18:近似点算子 Proximal Mapping
前面讲了梯度下降法,分析了其收敛速度,对于存在不可导的函数介绍了次梯度的计算方法以及次梯度下降法,这一节要介绍的内容叫做近似点算子(Proximal mapping),也是为了处理非光滑问题。
文章目录
- 1. 闭函数
- 2. 共轭函数
- 3. 近似点算子
- 4. 投影
- 5. 支撑函数、范数与距离
1. 闭函数
在引入闭函数(closed function)的概念之前,我们先回顾一下闭集的概念:集合 C \mathcal{C} C 是闭的,如果它包含边界,也即
x k ∈ C , x k → x ˉ ⇒ x ˉ ∈ C x^{k} \in \mathcal{C}, \quad x^{k} \rightarrow \bar{x} \quad \Rightarrow \quad \bar{x} \in \mathcal{C} xk∈C,xk→xˉ⇒xˉ∈C
并且有以下几个简单的原则可以保持集合闭的性质:
- 闭集的交集还是闭集;
- 有限个闭集的并集还是闭集;
- 如果 C \mathcal{C} C 是闭集,则线性映射的原象也是闭集,也即 { x ∣ A x ∈ C } \{x|Ax\in\mathcal{C}\} {x∣Ax∈C} 是闭集。
第 3 条原则反过来则不一定成立,也即如果 x ∈ C x\in\mathcal{C} x∈C 是闭集,那么 { A x ∣ x ∈ C } \{Ax|x\in\mathcal{C}\} {Ax∣x∈C} 则不一定是闭集,比如我们可以取函数 f ( x ) = 1 / x f(x)=1/x f(x)=1/x 的 epigraph 为闭集 C \mathcal{C} C,然而 ( x , y ) (x,y) (x,y) 向 x x x 轴的投影则是一个开集,严格表示与图示如下
C = { ( x 1 , x 2 ) ∈ R + 2 ∣ x 1 x 2 ≥ 1 } , A = [ 1 , 0 ] , A C = R + + \mathcal{C}=\left\{\left(x_{1}, x_{2}\right) \in \mathbb{R}_{+}^{2} | x_{1} x_{2} \geq 1\right\}, \quad A=[1,0], A \mathcal{C}=\mathbb{R}_{++} C={(x1,x2)∈R+2∣x1x2≥1},A=[1,0],AC=R++
| 第3条逆原则反例 | 第3条逆原则充分条件 |
|---|---|
 |
 |
当然,如果加一些其他的约束条件,则可以保证第 3 条反过来也成立: A C A\mathcal{C} AC 是闭的,如果
- C \mathcal{C} C 是闭的且为凸集;
- 并且 C \mathcal{C} C 不存在一个可以无穷延伸的方向(recession direction)属于 A A A 的零空间,也即 A y = 0 , x ^ ∈ C , x ^ + α y ∈ C , ∀ α > 0 ⇒ y = 0 A y=0, \hat{x} \in \mathcal{C}, \hat{x}+\alpha y \in \mathcal{C}, \forall \alpha>0 \Rightarrow y=0 Ay=0,x^∈C,x^+αy∈C,∀α>0⇒y=0,图示即如上。
然后我们就可以定义**闭函数(closed function)**了,函数 f f f 为闭的,如果他的 epigraph 为闭集或者他的所有下水平集为闭集。有以下两种简单的特殊情况:
- 如果 f f f 连续且定义域 dom f \text{dom}f domf 为闭的,则 f f f 为闭函数;
- 如果 f f f 连续且定义域 dom f \text{dom}f domf 为开的,则 f f f 为闭函数当且仅当其在 dom f \text{dom}f domf 边界处收敛至 ∞ \infty ∞。
例子 1: f ( x ) = x log x , dom f = R + , f ( 0 ) = 0 f(x)=x\log x,\quad\text{dom}f=R_+,f(0)=0 f(x)=xlogx,domf=R+,f(0)=0
例子 2:闭集的指示函数 δ C ( x ) = { 0 x ∈ C + ∞ o . w . \delta_C(x)=\begin{cases}0&x\in C\\ +\infty & o.w.\end{cases} δC(x)={0+∞x∈Co.w.
反例 3: f ( x ) = x log x , dom f = R + + f(x)=x\log x,\quad\text{dom}f=R_{++} f(x)=xlogx,domf=R++ 或者 f ( x ) = x log x , dom f = R + , f ( 0 ) = 1 f(x)=x\log x,\quad\text{dom}f=R_+,f(0)=1 f(x)=xlogx,domf=R+,f(0)=1 不是闭函数
反例 4:开集的指示函数不是闭函数
闭函数有一些有用的性质,比如:
- f f f 为闭函数当且仅当他的所有下水平集都是闭集;
- 如果 f f f 为闭函数,且下水平集有界,那么存在最小值点(minimizer)。
Theorem (Weierstrass) :假设集合 D ⊂ E D\subset \mathcal{E} D⊂E ( R n R^n Rn空间中有限维向量子空间) 非空且闭,并且连续函数 f : D → R f:D\to R f:D→R 的所有下水平集都有界,则 f f f 存在全局最小值点(global minimizer)。
对于闭函数来说也有一些原则可以保持闭的性质:
- 如果 f , g f,g f,g 均为闭函数,则 f + g f+g f+g 为闭函数
- 如果 f f f 为闭函数,则 f ( A x + b ) f(Ax+b) f(Ax+b) 为闭函数
- 如果任意 f α f_\alpha fα 都是闭函数,则 sup α f α ( x ) \sup_\alpha f_\alpha(x) supαfα(x) 为闭函数
2. 共轭函数
共轭函数(conjugate function) 前面已经讲过了,这里再简单回顾一遍。函数 f f f 的共轭函数定义为
f ⋆ ( y ) = sup x ∈ dom f ( y T x − f ( x ) ) f^\star(y)=\sup_{x\in\text{dom}f} (y^Tx-f(x)) f⋆(y)=x∈domfsup(yTx−f(x))
并且共轭函数有一些重要的性质:
- 共轭函数一定是闭函数,且为凸函数,不论 f f f 是否为凸函数或闭函数(因为 f ⋆ f^\star f⋆ 的 epigraph 可以看成很多个半空间的交集);
- (Fenchel’s inequality) f ( x ) + f ∗ ( y ) ≥ x ⊤ y , ∀ x , y f(x)+f^{*}(y) \geq x^{\top} y, \forall x, y f(x)+f∗(y)≥x⊤y,∀x,y
- (Legendre transform) 如果 f f f 为凸函数且为闭函数,则有 y ∈ ∂ f ( x ) ⇔ x ∈ ∂ f ∗ ( y ) ⇔ x ⊤ y = f ( x ) + f ∗ ( y ) y \in \partial f(x) \Leftrightarrow x \in \partial f^{*}(y) \Leftrightarrow x^{\top} y=f(x)+f^{*}(y) y∈∂f(x)⇔x∈∂f∗(y)⇔x⊤y=f(x)+f∗(y)
- 如果 f f f 为凸函数且为闭函数,则 f ⋆ ⋆ = f f^{\star\star}=f f⋆⋆=f
除此之外还有一些代数变换的原则,推导也都比较简单:
- f ( x 1 , x 2 ) = g ( x 1 ) + h ( x 2 ) , f ∗ ( y 1 , y 2 ) = g ∗ ( y 1 ) + h ∗ ( y 2 ) f\left(x_{1}, x_{2}\right)=g\left(x_{1}\right)+h\left(x_{2}\right), \quad f^{*}\left(y_{1}, y_{2}\right)=g^{*}\left(y_{1}\right)+h^{*}\left(y_{2}\right) f(x1,x2)=g(x1)+h(x2),f∗(y1,y2)=g∗(y1)+h∗(y2)
- f ( x ) = α g ( x ) , f ∗ ( y ) = α g ∗ ( y / α ) ( ★ ) f(x)=\alpha g(x), \quad f^{*}(y) {=} \alpha g^{*}(y / \alpha) \quad(\bigstar) f(x)=αg(x),f∗(y)=αg∗(y/α)(★)
- f ( x ) = g ( x ) + a ⊤ x + b f ∗ ( y ) = g ∗ ( y − a ) − b f(x)=g(x)+a^{\top} x+b \quad f^{*}(y)=g^{*}(y-a)-b f(x)=g(x)+a⊤x+bf∗(y)=g∗(y−a)−b
- f ( x ) = inf u + v = x ( g ( u ) + h ( v ) ) f ∗ ( y ) = g ∗ ( y ) + h ∗ ( y ) f(x)=\inf _{u+v=x}(g(u)+h(v)) \quad f^{*}(y)=g^{*}(y)+h^{*}(y) f(x)=infu+v=x(g(u)+h(v))f∗(y)=g∗(y)+h∗(y)
共轭函数的计算就不多举例子了,这里主要列出来后面用的比较多的而且比较重要的,其他的可以参考前面的笔记 6:
例子 1: C C C 为凸集,则指示函数 f ( x ) = δ C ( x ) f(x)=\delta_C(x) f(x)=δC(x),其共轭函数为支撑函数
f ⋆ ( y ) = sup { y T x ∣ x ∈ C } f^\star(y) = \sup\{y^Tx|x\in C\} f⋆(y)=sup{yTx∣x∈C}
如果求两次共轭函数也很容易得到:支撑函数的共轭函数为指示函数。
例子 2:范数 f ( x ) = ∥ x ∥ f(x)=\Vert x\Vert f(x)=∥x∥ 的共轭函数也是指示函数
f ⋆ ( y ) = { 0 ∥ y ∥ ∗ ≤ 1 ∞ otherwise f^\star(y) = \left\{\begin{array}{ll} 0 & \|y\|_{*} \leq 1 \\ \infty & \text { otherwise } \end{array}\right. f⋆(y)={0∞∥y∥∗≤1 otherwise
3. 近似点算子
首先给出来近似点算子(Proximal mapping)的定义:闭凸函数 f f f 的近似点算子定义为
prox f ( x ) = argmin u ( f ( u ) + 1 2 ∥ u − x ∥ 2 2 ) \operatorname{prox}_{f}(x)=\underset{u}{\operatorname{argmin}}\left(f(u)+\frac{1}{2}\|u-x\|_{2}^{2}\right) proxf(x)=uargmin(f(u)+21∥u−x∥22)
根据这个定义,实际上我们是在求解函数 g ( u ) = f ( u ) + 1 2 ∥ u − x ∥ 2 2 g(u)=f(u)+\frac{1}{2}\|u-x\|_{2}^{2} g(u)=f(u)+21∥u−x∥22 的最小值,由于 g g g 是闭函数且下水平集有界,因此最小值一定存在;同时由于 g g g 为强凸函数,因此最小值点唯一。
那么怎么理解这个算子函数 prox f ( x ) \text{prox}_f(x) proxf(x) 呢?可以看到这实际上是一个 prox f : R n → R n \text{prox}_f:R^n\to R^n proxf:Rn→Rn 的映射。如果 u = prox f ( x ) u=\text{prox}_f(x) u=proxf(x),则应该有 x − u ∈ ∂ f ( u ) x-u\in \partial f(u) x−u∈∂f(u)。下面看一些简单的例子。
例子 1:二次函数 A ⪰ 0 A\succeq 0 A⪰0
f ( x ) = 1 2 x T A x + b T x + c , prox t f ( x ) = ( I + t A ) − 1 ( x − t b ) f(x)=\frac{1}{2} x^{T} A x+b^{T} x+c, \quad \operatorname{prox}_{t f}(x)=(I+t A)^{-1}(x-t b) f(x)=21xTAx+bTx+c,proxtf(x)=(I+tA)−1(x−tb)
例子 2:欧几里得范数 f ( x ) = ∥ x ∥ 2 f(x)=\Vert x\Vert_2 f(x)=∥x∥2
prox t f ( x ) = { ( 1 − t / ∥ x ∥ 2 ) x ∥ x ∥ 2 ≥ t 0 otherwise \operatorname{prox}_{t f}(x)=\left\{\begin{array}{ll} \left(1-t /\|x\|_{2}\right) x & \|x\|_{2} \geq t \\ 0 & \text { otherwise } \end{array}\right. proxtf(x)={(1−t/∥x∥2)x0∥x∥2≥t otherwise
例子 3:Logarithmic barrier
f ( x ) = − ∑ i = 1 n log x i , prox t f ( x ) i = x i + x i 2 + 4 t 2 , i = 1 , … , n f(x)=-\sum_{i=1}^{n} \log x_{i}, \quad \operatorname{prox}_{t f}(x)_{i}=\frac{x_{i}+\sqrt{x_{i}^{2}+4 t}}{2}, \quad i=1, \ldots, n f(x)=−i=1∑nlogxi,proxtf(x)i=2xi+xi2+4t,i=1,…,n
上面是比较简单的例子,近似点算子也有一些很容易验证的代数运算规律:
- f ( [ x y ] ) = g ( x ) + h ( y ) , prox f ( [ x y ] ) = [ prox g ( x ) prox h ( y ) ] f\left(\left[\begin{array}{l} x \\ y \end{array}\right]\right)=g(x)+h(y), \quad \operatorname{prox}_{f}\left(\left[\begin{array}{l} x \\ y \end{array}\right]\right)=\left[\begin{array}{l} \operatorname{prox}_{g}(x) \\ \operatorname{prox}_{h}(y) \end{array}\right] f([xy])=g(x)+h(y),proxf([xy])=[proxg(x)proxh(y)]
- f ( x ) = g ( a x + b ) , prox f ( x ) = 1 a ( prox a 2 g ( a x + b ) − b ) f(x)=g(a x+b), \quad \operatorname{prox}_{f}(x)=\frac{1}{a}\left(\operatorname{prox}_{a^{2} g}(a x+b)-b\right) f(x)=g(ax+b),proxf(x)=a1(proxa2g(ax+b)−b) (注意 a ≠ 0 a\ne0 a=0 是标量)
- f ( x ) = λ g ( x / λ ) , prox f ( x ) = λ prox λ − 1 g ( x / λ ) ( ★ ) f(x)=\lambda g(x / \lambda), \quad \operatorname{prox}_{f}(x)=\lambda \operatorname{prox}_{\lambda^{-1} g}(x / \lambda) \quad(\bigstar) f(x)=λg(x/λ),proxf(x)=λproxλ−1g(x/λ)(★)
- f ( x ) = g ( x ) + a T x , prox f ( x ) = prox g ( x − a ) f(x)=g(x)+a^{T} x, \quad \quad \operatorname{prox}_{f}(x)=\operatorname{prox}_{g}(x-a) f(x)=g(x)+aTx,proxf(x)=proxg(x−a)
- f ( x ) = g ( x ) + μ 2 ∥ x − a ∥ 2 2 , prox f ( x ) = prox θ g ( θ x + ( 1 − θ ) a ) f(x)=g(x)+\frac{\mu}{2}\|x-a\|_{2}^{2}, \quad \operatorname{prox}_{f}(x)=\operatorname{prox}_{\theta g}(\theta x+(1-\theta) a) f(x)=g(x)+2μ∥x−a∥22,proxf(x)=proxθg(θx+(1−θ)a),其中 μ > 0 , θ = 1 / ( 1 + μ ) \mu>0,\theta=1/(1+\mu) μ>0,θ=1/(1+μ)
- f ( x ) = g ( A x + b ) f(x)=g(Ax+b) f(x)=g(Ax+b),对于一般的 A A A 并不能得到比较好的性质,但如果 A A T = ( 1 / α ) I AA^T=(1/\alpha)I AAT=(1/α)I,则有
prox f ( x ) = ( I − α A T A ) x + α A T ( prox α − 1 g ( A x + b ) − b ) = x − α A T ( A x + b − prox α − 1 g ( A x + b ) ) \begin{aligned}\operatorname{prox}_{f}(x) &=\left(I-\alpha A^{T} A\right) x+\alpha A^{T}\left(\operatorname{prox}_{\alpha^{-1} g}(A x+b)-b\right) \\&=x-\alpha A^{T}\left(A x+b-\operatorname{prox}_{\alpha^{-1} g}(A x+b)\right)\end{aligned} proxf(x)=(I−αATA)x+αAT(proxα−1g(Ax+b)−b)=x−αAT(Ax+b−proxα−1g(Ax+b))
前面几条都比较容易证明,最后一条证明可以等价于求解
minimize g ( y ) + 1 2 ∥ u − x ∥ 2 2 subject to A u + b = y \begin{aligned}\text { minimize } \quad& g(y)+\frac{1}{2}\|u-x\|_{2}^{2}\\\text { subject to } \quad& A u+b=y\end{aligned} minimize subject to g(y)+21∥u−x∥22Au+b=y
可以先求解 x x x 向超平面 A u + b = y Au+b=y Au+b=y 投影来消去 u u u,然后再计算 prox f ( y ) \text{prox}_f(y) proxf(y)。
除此之外,有一个非常重要的等式:
Moreau decomposition:
x = prox f ( x ) + prox f ∗ ( x ) for all x x=\operatorname{prox}_{f}(x)+\operatorname{prox}_{f^{*}}(x) \quad\text { for all } x x=proxf(x)+proxf∗(x) for all x
Remarks:为什么说这个式子重要呢?因为他把原函数和共轭函数的 proximal mapping 联系起来了,如果其中一个比较难计算,那么我们可以通过另一个来计算。这个式子可以怎么理解呢?可以看成是一种正交分解,举个栗子,如果我们取一个子空间 L L L,他的正交空间为 L ⊥ L^\perp L⊥,令函数 f f f 为子空间 L L L 的指示函数也即 f = δ L f=\delta_L f=δL,那么很容易验证共轭函数 f ⋆ = δ L ⊥ f^\star=\delta_{L^\perp} f⋆=δL⊥。而根据定义也可以得到 prox f ( x ) \text{prox}_f(x) proxf(x) 恰好就是 x x x 在子空间 L L L 上的投影,记为 P L ( x ) = prox f ( x ) P_L(x)=\text{prox}_f(x) PL(x)=proxf(x),同样的 P L ⊥ ( x ) = prox f ⋆ ( x ) P_{L^\perp}(x)=\text{prox}_{f^\star}(x) PL⊥(x)=proxf⋆(x),因此上面的 Moreau decomposition 就可以写为 x = P L ( x ) + P L ⊥ ( x ) x=P_L(x)+P_{L^\perp}(x) x=PL(x)+PL⊥(x),这正好就是一个正交分解。可以根据下图理解
如果对原始的 Moreau decomposition 做简单的代数变换,就可以得到 λ > 0 \lambda>0 λ>0
x = prox λ f ( x ) + λ prox λ − 1 f ∗ ( x / λ ) for all x x=\operatorname{prox}_{\lambda f}(x)+\lambda \operatorname{prox}_{\lambda^{-1} f^{*}}(x / \lambda) \quad \text { for all } x x=proxλf(x)+λproxλ−1f∗(x/λ) for all x
证明过程用到了共轭函数的性质 ( λ f ) ⋆ ( y ) = λ f ⋆ ( y / λ ) (\lambda f)^{\star}(y)=\lambda f^{\star}(y / \lambda) (λf)⋆(y)=λf⋆(y/λ)。
后面两个小节则主要是近似点算子的应用,一个是计算投影,另一个是与支撑函数、距离相关的内容。
4. 投影
为什么突然讲到投影呢?因为对指示函数应用近似点算子,实质上就是在计算投影。举个栗子就明白了:对于集合 C C C 与集合外一点 x x x, x x x 向集合 C C C 的投影可以表示为
minimize 1 2 ∥ y − x ∥ 2 2 subject to y ∈ C \begin{aligned}\text { minimize } \quad& \frac{1}{2}\|y-x\|_{2}^{2}\\\text { subject to } \quad& y\in C\end{aligned} minimize subject to 21∥y−x∥22y∈C
若投影点为 y ⋆ y^\star y⋆,则这可以等价表示为
y ⋆ = arg min y 1 2 ∥ y − x ∥ 2 2 + δ C ( y ) = prox δ ( x ) \begin{aligned}y^\star &= \arg\min_y \frac{1}{2}\|y-x\|_{2}^{2}+\delta_C(y) \\&= \text{prox}_{\delta}(x)\end{aligned} y⋆=argymin21∥y−x∥22+δC(y)=proxδ(x)
因此 prox δ ( x ) \text{prox}_{\delta}(x) proxδ(x) 就是 x x x 向集合 C C C 的投影点(对于 x ∈ C x\in C x∈C 同样成立)。那么只要我们取不同的 C C C,就能得到各种类型集合的投影表达式,下面举一些例子。
超平面: C = { x ∣ a T x = b } C=\{x|a^Tx=b\} C={x∣aTx=b} with a ≠ 0 a\ne0 a=0
P C ( x ) = x + b − a T x ∥ a ∥ 2 2 a P_{C}(x)=x+\frac{b-a^{T} x}{\|a\|_{2}^{2}} a PC(x)=x+∥a∥22b−aTxa
仿射集: C = { x ∣ A x = b } ( with A ∈ R p × n and rank ( A ) = p ) C=\{x | A x=b\}\left(\text { with } A \in \mathbf{R}^{p \times n} \text { and } \operatorname{rank}(A)=p\right) C={x∣Ax=b}( with A∈Rp×n and rank(A)=p)
P C ( x ) = x + A T ( A A T ) − 1 ( b − A x ) P_{C}(x)=x+A^{T}\left(A A^{T}\right)^{-1}(b-A x) PC(x)=x+AT(AAT)−1(b−Ax)
半空间: C = { x ∣ a T x ≤ b } C=\{x|a^Tx\le b\} C={x∣aTx≤b} with a ≠ 0 a\ne0 a=0
P C ( x ) = { x + b − a T x ∥ a ∥ 2 2 a if a T x > b x if a T x ≤ b P_{C}(x)=\begin{cases}x+\frac{b-a^{T} x}{\|a\|_{2}^{2}} a & \text {if } a^{T} x>b \\ x & \text {if } a^{T} x \leq b\end{cases} PC(x)={x+∥a∥22b−aTxaxif aTx>bif aTx≤b
矩形: C = [ l , u ] = { x ∈ R n ∣ l ≤ x ≤ u } C=[l, u]=\left\{x \in \mathbf{R}^{n} | l \leq x \leq u\right\} C=[l,u]={x∈Rn∣l≤x≤u}
P C ( x ) k = { l k x k ≤ l k x k l k ≤ x k ≤ u k u k x k ≥ u k P_{C}(x)_{k}=\left\{\begin{array}{ll}l_{k} & x_{k} \leq l_{k} \\x_{k} & l_{k} \leq x_{k} \leq u_{k} \\u_{k} & x_{k} \geq u_{k}\end{array}\right. PC(x)k=⎩⎨⎧lkxkukxk≤lklk≤xk≤ukxk≥uk
非负象限: C = R + n C=R_+^n C=R+n
P C ( x ) = x + = ( max { 0 , x 1 } , max { 0 , x 2 } , … , max { 0 , x n } ) P_{C}(x)=x_{+}=\left(\max \left\{0, x_{1}\right\}, \max \left\{0, x_{2}\right\}, \ldots, \max \left\{0, x_{n}\right\}\right) PC(x)=x+=(max{0,x1},max{0,x2},…,max{0,xn})
概率单形: C = { x ∣ 1 T x = 1 , x ≥ 0 } C=\left\{x | \mathbf{1}^{T} x=1, x \geq 0\right\} C={x∣1Tx=1,x≥0}
P C ( x ) = ( x − λ 1 ) + P_{C}(x)=(x-\lambda \mathbf{1})_{+} PC(x)=(x−λ1)+
其中 λ \lambda λ 由以下方程解出
1 T ( x − λ 1 ) + = ∑ i = 1 n max { 0 , x k − λ } = 1 \mathbf{1}^{T}(x-\lambda \mathbf{1})_{+}=\sum_{i=1}^{n} \max \left\{0, x_{k}-\lambda\right\}=1 1T(x−λ1)+=i=1∑nmax{0,xk−λ}=1
这个的证明有一点难度,关键是首先要把约束条件 x ≥ 0 x\ge0 x≥0 转换为指示函数表示
minimize 1 2 ∥ y − x ∥ 2 2 + δ R + n ( y ) subject to 1 T y = 1 \begin{aligned}\text { minimize } \quad& \frac{1}{2}\|y-x\|_{2}^{2} + \delta_{R_+^n}(y) \\\text { subject to } \quad& \mathbf{1}^{T} y=1\end{aligned} minimize subject to 21∥y−x∥22+δR+n(y)1Ty=1
然后将拉格朗日函数分解成求和的形式
1 2 ∥ y − x ∥ 2 2 + δ R + n ( y ) + λ ( 1 T y − 1 ) = ∑ k = 1 n ( 1 2 ( y k − x k ) 2 + δ R + ( y k ) + λ y k ) − λ \begin{array}{l}\frac{1}{2}\|y-x\|_{2}^{2}+\delta_{\mathbf{R}_{+}^{n}}(y)+\lambda\left(\mathbf{1}^{T} y-1\right) \\\quad=\quad \sum_{k=1}^{n}\left(\frac{1}{2}\left(y_{k}-x_{k}\right)^{2}+\delta_{\mathbf{R}_{+}}\left(y_{k}\right)+\lambda y_{k}\right)-\lambda\end{array} 21∥y−x∥22+δR+n(y)+λ(1Ty−1)=∑k=1n(21(yk−xk)2+δR+(yk)+λyk)−λ
对上面这个求和项进行分情况讨论就能得到解析表达式了,不过真的很繁琐。
超平面与矩形交集: C = { x ∣ a T x = b , l ⪯ x ⪯ u } C=\{x|a^Tx=b,l\preceq x\preceq u\} C={x∣aTx=b,l⪯x⪯u}
P C ( x ) = P [ l , u ] ( x − λ a ) P_{C}(x)=P_{[l,u]}(x-\lambda a) PC(x)=P[l,u](x−λa)
其中 λ \lambda λ 由以下方程解出
a T P [ l , u ] ( x − λ a ) = b a^{T} P_{[l, u]}(x-\lambda a)=b aTP[l,u](x−λa)=b
证明跟上面的概率单形是类似的,也需要拆写成多项求和的形式分别求解。
欧几里得球: C = { x ∣ ∥ x ∥ 2 ≤ 1 } C=\{x| \Vert x\Vert_2\le1\} C={x∣∥x∥2≤1}
P C ( x ) = { x ∥ x ∥ 2 if ∥ x ∥ 2 > 1 x if ∥ x ∥ 2 ≤ 1 P_{C}(x)=\begin{cases}\frac{x}{\|x\|_{2}} & \text {if } \Vert x\Vert_2>1 \\ x & \text {if } \Vert x\Vert_2\le1\end{cases} PC(x)={∥x∥2xxif ∥x∥2>1if ∥x∥2≤1
1 范数球: C = { x ∣ ∥ x ∥ 1 ≤ 1 } C=\{x| \Vert x\Vert_1\le1\} C={x∣∥x∥1≤1}
若 ∥ x ∥ 1 ≤ 1 \Vert x\Vert_1\le1 ∥x∥1≤1 则 P C ( x ) = x P_C(x)=x PC(x)=x;否则
P C ( x ) k = sign ( x k ) max { ∣ x k ∣ − λ , 0 } = { x k − λ x k > λ 0 − λ ≤ x k ≤ λ x k + λ x k < − λ P_{C}(x)_{k}=\operatorname{sign}\left(x_{k}\right) \max \left\{\left|x_{k}\right|-\lambda, 0\right\}=\left\{\begin{array}{ll}x_{k}-\lambda & x_{k}>\lambda \\0 & -\lambda \leq x_{k} \leq \lambda \\x_{k}+\lambda & x_{k}<-\lambda\end{array}\right. PC(x)k=sign(xk)max{∣xk∣−λ,0}=⎩⎨⎧xk−λ0xk+λxk>λ−λ≤xk≤λxk<−λ
其中 λ \lambda λ 由以下等式获得
∑ k = 1 n max { ∣ x ∣ k − λ , 0 } = 1 \sum_{k=1}^n \max \{\vert x\vert_k-\lambda, 0\}=1 k=1∑nmax{∣x∣k−λ,0}=1
证明业与前面的类似,需要写成求和项的形式,然后对每一项求解。
二阶锥: C = { ( x , t ) ∈ R n × 1 ∣ ∥ x ∥ 2 ≤ t } C=\{(x,t)\in R^{n\times 1}| \Vert x\Vert_2 \le t \} C={(x,t)∈Rn×1∣∥x∥2≤t}
P C ( x , t ) = { ( x , t ) if ∥ x ∥ 2 ≤ t ( 0 , 0 ) if ∥ x ∥ 2 ≤ − t t + ∥ x ∥ 2 2 ∥ x ∥ 2 [ x ∥ x ∥ 2 ] if ∥ x ∥ 2 > ∣ t ∣ P_{C}(x,t)=\begin{cases}(x,t) & \text {if } \Vert x\Vert_2\le t \\ (0,0) & \text {if } \Vert x\Vert_2\le -t \\\frac{t+\|x\|_{2}}{2\|x\|_{2}}\left[\begin{array}{c} x \\ \|x\|_{2} \end{array}\right] & \text {if } \Vert x\Vert_2> \vert t\vert \end{cases} PC(x,t)=⎩⎪⎪⎨⎪⎪⎧(x,t)(0,0)2∥x∥2t+∥x∥2[x∥x∥2]if ∥x∥2≤tif ∥x∥2≤−tif ∥x∥2>∣t∣
正定锥: C = S + n C=S^n_+ C=S+n
P C ( X ) = ∑ i = 1 n max { 0 , λ i } q i q i T P_{C}(X)=\sum_{i=1}^{n} \max \left\{0, \lambda_{i}\right\} q_{i} q_{i}^{T} PC(X)=i=1∑nmax{0,λi}qiqiT
其中 X = ∑ i λ i q i q i T X=\sum_i \lambda_i q_iq_i^T X=∑iλiqiqiT
5. 支撑函数、范数与距离
这一小节标题看起来很复杂,牵涉到了支撑函数、范数、到集合的距离,但实际上都还是在计算投影,为什么这么说呢?回忆一下,支撑函数的共轭函数是不是 δ \delta δ 函数?范数的共轭函数是不是 δ \delta δ 函数?到集合的距离是不是就等于到投影点的距离?所以这一小节是上一小节“投影”的自然延伸,其中为了把原函数与共轭函数联系在一起,用到了 Moreau decomposition。我们一个一个来看。
x = prox f ( x ) + prox f ∗ ( x ) for all x x=\operatorname{prox}_{f}(x)+\operatorname{prox}_{f^{*}}(x) \quad\text { for all } x x=proxf(x)+proxf∗(x) for all x
支撑函数: f ( x ) = sup y ∈ C x T y , f ⋆ ( y ) = δ C ( y ) f(x)=\sup_{y\in C}x^Ty,f^\star(y)=\delta_C(y) f(x)=supy∈CxTy,f⋆(y)=δC(y),因此近似点算子为
prox t f ( x ) = x − t prox t − 1 f ∗ ( x / t ) = x − t P C ( x / t ) \begin{aligned}\operatorname{prox}_{t f}(x) &=x-t \operatorname{prox}_{t^{-1} f^{*}}(x / t) \\&=x-t P_{C}(x / t)\end{aligned} proxtf(x)=x−tproxt−1f∗(x/t)=x−tPC(x/t)
范数: f ( x ) = ∥ x ∥ , f ⋆ ( y ) = δ B ( y ) f(x)=\Vert x\Vert,f^\star(y)=\delta_B(y) f(x)=∥x∥,f⋆(y)=δB(y),其中 B = { y ∣ ∥ y ∥ ⋆ ≤ 1 } B=\{y| \Vert y\Vert_\star \le 1\} B={y∣∥y∥⋆≤1},近似点算子为
prox t f ( x ) = x − t prox t − 1 f ∗ ( x / t ) = x − t P B ( x / t ) = x − P t B ( x ) \begin{aligned}\operatorname{prox}_{t f}(x) &=x-t \operatorname{prox}_{t^{-1} f^{*}}(x / t) \\&=x-t P_{B}(x / t) \\&=x- P_{tB}(x)\end{aligned} proxtf(x)=x−tproxt−1f∗(x/t)=x−tPB(x/t)=x−PtB(x)
其中 t B = { y ∣ ∥ y ∥ ⋆ ≤ t } tB=\{y| \Vert y\Vert_\star \le t\} tB={y∣∥y∥⋆≤t}
与一点的距离: f ( x ) = ∥ x − a ∥ f(x)=\Vert x-a\Vert f(x)=∥x−a∥,可以取 g ( x ) = ∥ x ∥ g(x)=\Vert x\Vert g(x)=∥x∥
prox t f ( x ) = a + prox t g ( x − a ) = a + x − a − t P B ( x − a t ) = x − P t B ( x − a ) \begin{aligned}\operatorname{prox}_{t f}(x) &=a + \operatorname{prox}_{tg}(x-a) \\&=a+x-a-tP_B(\frac{x-a}{t}) \\&=x- P_{tB}(x-a)\end{aligned} proxtf(x)=a+proxtg(x−a)=a+x−a−tPB(tx−a)=x−PtB(x−a)
到集合的距离:到闭凸集 C C C 的距离定义为 d ( x ) = inf y ∈ C ∥ x − y ∥ 2 d(x)=\inf_{y\in C}\Vert x-y\Vert_2 d(x)=infy∈C∥x−y∥2
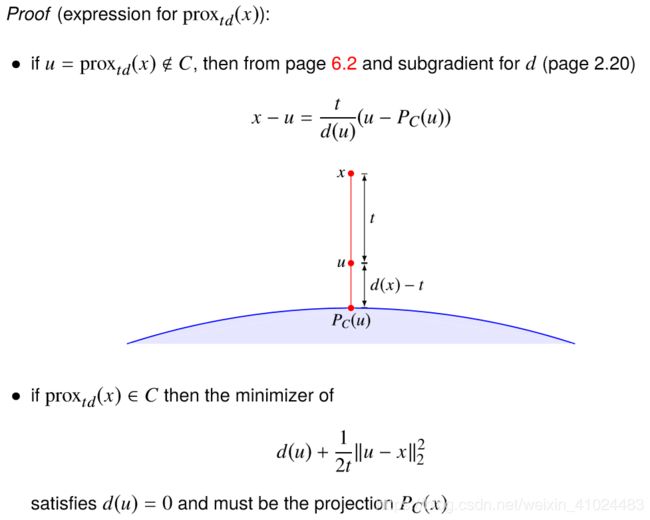
prox t d ( x ) = { x + t d ( x ) ( P C ( x ) − x ) d ( x ) ≥ t P C ( x ) otherwise \operatorname{prox}_{t d}(x)=\left\{\begin{array}{ll}x+\frac{t}{d(x)}\left(P_{C}(x)-x\right) & d(x) \geq t \\P_{C}(x) & \text { otherwise }\end{array}\right. proxtd(x)={x+d(x)t(PC(x)−x)PC(x)d(x)≥t otherwise
如果是距离取平方 f ( x ) = d ( x ) 2 / 2 f(x)=d(x)^2/2 f(x)=d(x)2/2,则有
prox t f ( x ) = 1 1 + t x + t 1 + t P C ( x ) \operatorname{prox}_{t f}(x)=\frac{1}{1+t} x+\frac{t}{1+t} P_{C}(x) proxtf(x)=1+t1x+1+ttPC(x)
这个证明贴在下面
最后给我的博客打个广告,欢迎光临
https://glooow1024.github.io/
https://glooow.gitee.io/
前面的一些博客链接如下
凸优化专栏
凸优化学习笔记 1:Convex Sets
凸优化学习笔记 2:超平面分离定理
凸优化学习笔记 3:广义不等式
凸优化学习笔记 4:Convex Function
凸优化学习笔记 5:保凸变换
凸优化学习笔记 6:共轭函数
凸优化学习笔记 7:拟凸函数 Quasiconvex Function
凸优化学习笔记 8:对数凸函数
凸优化学习笔记 9:广义凸函数
凸优化学习笔记 10:凸优化问题
凸优化学习笔记 11:对偶原理
凸优化学习笔记 12:KKT条件
凸优化学习笔记 13:KKT条件 & 互补性条件 & 强对偶性
凸优化学习笔记 14:SDP Representablity
最优化方法 15:梯度方法
最优化方法 16:次梯度
最优化方法 17:次梯度下降法
最优化方法 18:近似点算子 Proximal Mapping
最优化方法 19:近似梯度下降
最优化方法 20:对偶近似点梯度下降法
最优化方法 21:加速近似梯度下降方法
最优化方法 22:近似点算法 PPA
最优化方法 23:算子分裂法 & ADMM
最优化方法 24:ADMM