KMP模式匹配算法&next数组优化代码
KMP是为了解决朴素匹配算法的低效率问题。
例如:
朴素算法匹配:
观察字串第一个字母a于后面的bcdex都不相等,而在①匹配可知,主串和子串的前五位分别相等,意味着子串的首字母a不可能与主串的第2位到第5位的字符相等,所以朴素算法中的②③斯⑤都是多余的。
例如:
T[1]=a,T[2]=b;S[2]=b;
∵T[1]≠T[2]且T[2]=S[2];∴T[1]≠S[2]
同样,在上图子串中 首字符a与后面字符均不相等的前提下,子串的a与主串后面的b,c,d,e也都可以在①之后就可以确定是不相等的,所以在朴素算法中的②③④⑤是多余的,只需保留①⑥即可。而保留⑥是因为在中匹配时,T[6]≠S[6],尽管知道T[1]≠T[6],可也无法确定T[1]≠S[6];所以仍需要判断一下。
当子串中含有重复字符时:
例如:S=abcababca,T=abcabx
根据 上面的描述:T中首字符a与后面的b,c不相等,所以②③是多余的。
∵T[1]=T[4],T[2]=T[5],在①时,T[4],T[5]已经和S中的S[4]S[5]匹配过是相等的
∴T[1]=S[4],T[2]=S[5]
因此④⑤这两个步骤也是多余的。
在朴素算法中,i是不断回溯的,从①-6,到②-2,③-3,④-4,⑤-5,到了⑥,i又变成6.KMP就是为了让没必要的回溯不发生。
也就是i的值不可以变小,那么要考虑的变化就是j的值,在上面的推导就知道,j的值是由子串中是否有重复字符来决定的。
例如:
T=abcdex,T没有重复字符,j就从6变回了1.而
T=abcabx,前缀的ab和最后x之前串的后缀ab是相等的,因此j就由6变成了3.因此,j值的多少取决于当前字符之前的串的前后缀的相似度。
现在把T串各个位置的j值的变化定义为一个next数组,那么next数组长度就是子串的长度,所以:
0,j=1
next={ Max{k|1
1,其他情况
要匹配的子串的next数组代码实现:
void get_next(String T, int *next)
{
int i, j;
i = 1;
j = 0;
next[1] = 0;
while (i < T[0])//T[0]表示子串长度
{
if (j == 0 || T[i] == T[j])
{
i++;
j++;
next[i] = j;
}
else
j = next[j];//若字符不相同,则j值回溯
}
}KMP算法改进:
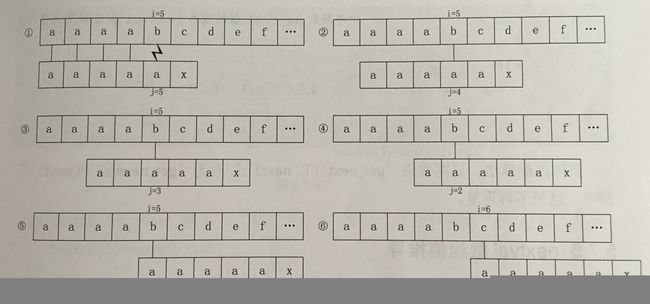
当S=aaaabcde T=aaaaax,其next数组的值为{012345}
其实,当中的②③④⑤ 步骤是多余的,因为T中第二,三,四,五位置的字母都与首位a相等,那么既可以用首位next[1]的值去代替与它相等的字符后续next[j]的值。
代码:
void get_nextval(string T, int *nextval)
{
int i = 1;
int j = 0;
nextval[1] = 0;
while (i < T.length())
{
if (j == 0 || T[i] == T[j])
{
i++;
j++;
if (T[i] != T[j]])//若当前字符与前缀不同
nextval[i] = j;//则当前的j为nextval在i位置的值
else
nextval[i] = nextval[j];//如果相同,则将前缀的nextval[i]值赋值给nextval在i位置的值
}
else
j = nextval[j];
}
}下面是从0开始匹配的完整代码。
完整代码:
#include
#include
using namespace std;
/*void get_next(string t, int next[])
{
int i = 0;
int j = -1;
next[0] = -1;
while (i < t.length())
{
if (j == -1 || t[i] == t[j])//t[i]表示后缀的单个字符,t[j]表示前缀的单个字符
{
i++;
j++;
next[i] = j;
}
else
{
j = next[j];//若字符不想的,则j值回溯,即缩短比较的前后缀长度。
}
}
}
*/
void get_nextval(string t, int nextval[])
{
int i = 0;
int j = -1;
nextval[0] = -1;
while (i < t.length())
{
if (j == -1 || t[i] == t[j])
{
i++;
j++;
if (t[i != t[j]])//若当前字符与前缀不同
nextval[i] = j;//则当前的j为nextval在i位置的值
else
nextval[i] = nextval[j];//如果相同,则将前缀的nextval[i]值赋值给nextval在i位置的值
}
else
j = nextval[j];
}
}
int Index(string s, string t, int pos)
{
int i = pos;//从pos位置开始匹配
int j = 1;//子串当前位置下标值
int size1 = s.length();
int size2 = t.length();
int next[222];
get_nextval(t, next);
while (i < size1&&j size2-1)
return i - size2+1;
else
return 0;
}
int main()
{
string S, T;
cin >> S >> T;
int num = Index(S, T, 0);
if (!num)
cout << "NO found!" << endl;
else
cout << "从" << num-1 << "开始查找" << endl;
return 0;
} next数组的性质,有
i%( i-next[i] )==0&&next[i] !=0 , 则说明字符串前i位循环,而且循环节长度为:i-next[i],循环次数为: i/( i-next[i]);