线性规划网络流 ：工厂最大效益——单纯形算法【超详+题解】

问题：某食品加工厂一共有三个车间，第一车间用 1 个单位的原料 N 可以加工 5 个单位的产品 A 或 2 个单位的产品 B。产品 A 如果直接售出，售价为 10 元，如果在第二车间继续加工，则需要额外加工费 5 元，加工后售价为 19 元。产品 B 如果直接售出，售价 16 元，如果在第三车间继续加工，则需要额外加工费 4 元，加工后售价为 24 元。原材料 N 的单位购入价为 5 元，每工时的资是15 元，第一车间加工一个单位的 N，需要 0.05 个工时，第二车间加工一个单位需要 0.1 工时，第三车间加工一个单位需要 0.08工时。每个月最多能得到 12000 单位的原材料 N，工时最多为 1000 工时。如何安排生产，才能使工厂的效益最大呢？

这种题先想想，它就是一道高中数学题，所以先不管代码怎么设计，先把目标函数和约束条件推出来啦~

先来设变量、；

x1：产品 A 的售出量。
x2：产品 A 在第二车间加工后的售出量。
x3：产品 B 的售出量。
x4：产品 B 在第三车间加工后的售出量。
x5：第一车间所用原材料数量。
目标函数和约束条件如下：

maxz=10x1+12.5x2+16x3+18.8x4-5.75x5;

约束条件：

   x1+x2-5x5=0;

{  x3+x4-2x5=0;

   x5≤12000；

  0.05x5+0.1x3+0.08x4≤1000；

  xi(i=1, 2, 3, 4, 5)

好了，最重要的都能写出来后面就是算法和设计代码的问题了。

解决这种线性规划问题一般都采用单纯形算法，即用一个单纯形表来存储上面推出来的条件。

首先在存储之前需要将线性规划转化为标准型。

把不等式变为等式，如果目标函数是要求最小值，则需要转化为最大值，即添加一个负号，在最好求出来的最优解添加一个负号。这道题不需要这样的操作。

约束条件中等式中只出现一个等式的变量为基本变量，其余为非基本变量，在目标函数中的非基本变量的系数为检验数，目标函数若有基本变量，则将基本变量用非基本变量来表示：

maxz=2.5x2+2.8x4+76.5x5;

约束条件：

   x1+x2-5x5=0;

   x3+x4-2x5=0;

 { x5+x6=12000；

  0.05x5+0.1x3+0.08x4+x7=1000；

  xi≥0(i=1,2,3,4,5,6,7)

单纯形表 ：

 （1）判断是否得到最优解：

①：若所有的检验数都小于零，则已获得最优解，算法结束。

②：若检验数中存在正数，而某一正数所对应的列向量的各分量都小于等于零，则线性规划问题无界，算法结束。

③：若检验数中有正数，且他们所对应的列向量有正数，则继续下面的计算。

（2）选入基变量

选取所有正检验数中最大的一个，记为 Ce，其对应的非基本变量为 Xe称为入基变量，Xe对应的列向量[a1e，a2e，…，ame]^T.为入基列.

(3) 选离基变量

选离基变量
选取“常数列元素/入基列元素”正比值的最小者，所对应的非基本变量 xk为离基变量。xk对应的行向量[ak1，ak2，…，akn]为离基行。

(4)换基变换

（5）换基变换
在单纯形表上将入基变量和离基变量互换位置，即 x3 和 x5 交换位置，换基变换之后如图 7-5 所示。

（6）计算新的单纯形表

按以下方法计算新的单纯形表：
4 个特殊位置如下：
• 入基列=−原值/交叉位值（不包括交叉位）。
• 离基行=原值/交叉位值（不包括交叉位）。
• 交叉位=原值取倒数。
• c0 位=原值+同行入基列元素*同列离基行元素/交叉位值。

一般位置元素=原值−同行入基列元素*同列离基行元素/交叉位值。

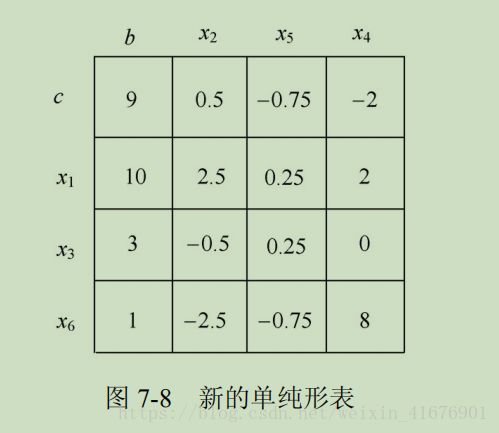
新表：

然后继续从（1）开始，直到 找到最优解或者判定无界停止。

代码：

#include
#include
#include
#include
using namespace std;
float kernel[100][100];
char FJL[100] = {};
char JL[100] = {};
int n, m;
void print()
{
	cout << endl;
	cout << "---------单纯形表如下：----------" << endl;
	cout << "   ";
	cout << setw(7) << "b ";
	for (int i = 1; i <= m; i++)
		cout << setw(7) << "X" << FJL[i];
	cout << endl;
	cout << "c ";
	for (int i = 0; i <= n; i++)
	{
		if (i >= 1)
		{
			cout << "X" << JL[i];
		}
		for (int j = 0; j <= m; j++)
			cout << setw(7) << kernel[i][j] << " ";
		cout << endl;
	}
}
void DCXA()
{
	float max1, max2, min;
	int e = -1, k = -1;
	while (1)
	{
		max1 = 0; max2 = 0;
		min = 99999999.9;
		//入基变量
		for (int i = 1; i <= m; i++)
		{
			if (max1 < kernel[0][i])
			{
				max1 = kernel[0][i];
				e = i;
			}
		}
		if (max1 <= 0)
		{
			cout << endl;
			cout << "获得最优解： " << kernel[0][0] << endl;
			break;
		}
		for (int i = 1; i <= n; i++)
		{
			if (max2 < kernel[i][e])
			{
				max2 = kernel[i][e];
			}
			float temp = kernel[i][0] / kernel[i][e];
			if (temp > 0 && temp < min)
			{
				min = temp;
				k = i;
			}
		}
		cout << "入基变量" << "X" << FJL[e] << " ";
		cout << "离基变量" << "X" << JL[k] << " ";
		if (max2 == 0)
		{
			cout << "解无届" << endl;
			break;
		}
		//变基变换
		char temp = FJL[e];
		FJL[e] = JL[k];
		JL[k] = temp;
		//更新非入基列和非离基行的所有位置的元素
		for (int i = 0; i <= n; i++)
		{
			if (i != k)
			{
				for (int j = 0; j <= m; j++)
				{
					if (j != e)
					{
						if (i == 0 && j == 0)
							kernel[i][j] = kernel[i][j] + kernel[i][e] * kernel[k][j] / kernel[k][e];
						else
							kernel[i][j] = kernel[i][j] - kernel[i][e] * kernel[k][j] / kernel[k][e];
					}
				}
			}
		}
		//更新入基列元素（不包括交叉为）
		for (int i = 0; i <= n; i++)
		{
			if (i != k)
			{
				kernel[i][e] = -kernel[i][e] / kernel[k][e];
			}
		}
		//更新离基行元素（不包括交叉位）
		for (int i = 0; i <= m; i++)
		{
			if (i != e)
			{
				kernel[k][i] = kernel[k][i] / kernel[k][e];
			}
		}
		kernel[k][e] = 1 / kernel[k][e];
		print();
	}
}
int main()
{
	//非基本变量个数和非基本变量下标
	cin >> m;
	for (int i = 1; i <= m; i++)
		cin >> FJL[i];
	//基本变量个数和基本变量下标
	cin >> n;
	//标准型初始单纯形表参数
	for (int i = 1; i <= n; i++)
		cin >> JL[i];
	for (int i = 0; i <= n; i++)
	{
		for (int j = 0; j <= m; j++)
			cin >> kernel[i][j];
	}
	print();
	DCXA();
	return  0;
}