李宏毅2020机器学习作业1——Linear Regression
—————————————————————————————————————————————
开始之前声明：本文参考了李宏毅机器学习作业说明（需）,基本上是将代码复现了一遍，说明中用的是google colab（由谷歌提供的免费的云平台），我用的是Jupyter Notebook。
—————————————————————————————————————————————
本文所用到的资料百度网盘自取点击下载，提取码：j9f8。请将所需资料下载好，确保有train.csv和test.csv两个文件，并保存到自己的目录当中。
————————————————————————————————————————————
【博主的环境：Anaconda3 +Jupyter Notebook，python3.6.8】
————————————————————————————————————————————
作业要求：由每天前9个小时的18个空气的影响因素（如：NO，CO，SO2，PM2.5等等）来预测第10个小时的PM2.5，train.csv是一年的数据，每个月取了20天，每天24小时
————————————————————————————————————————————
现在开始跟着我一步步copy~~
开始之前先导入需要的库：
- sys：该模块提供对解释器使用或维护的一些变量的访问，以及与解释器强烈交互的函数
- pandas：一个强大的分析结构化数据的工具集
- numpy： Python的一个扩展程序库，支持大量的维度数组与矩阵运算
- math：数学运算的库
没有库的请自行安装（Jupyter Notebook安装方法：进入自己的环境，conda install 库名字 即可）
import sys
import pandas as pd
import numpy as np
import math
现在导入train数据
#导入数据（前面‘’为数据存放路径，后面big5对字符串进行编码转换）
data = pd.read_csv('E:/jupyter/data/hw1/train.csv',encoding='big5')
我们的数据是csv格式用excel打开会出现乱码，可以用Notepad++打开
对数据进行处理，取第4列开始的数据
#分割出前3列，从第4列开始将数据存到data
data = data.iloc[:, 3:]
data[data == 'NR'] = 0
raw_data = data.to_numpy()
print(raw_data)
运行之后结果，对照train数据可以看出，前3列数据已经被删掉了
[['14' '14' '14' ... '15' '15' '15']
['1.8' '1.8' '1.8' ... '1.8' '1.8' '1.8']
['0.51' '0.41' '0.39' ... '0.35' '0.36' '0.32']
...
['36' '55' '72' ... '118' '100' '105']
['1.9' '2.4' '1.9' ... '1.5' '2' '2']
['0.7' '0.8' '1.8' ... '1.6' '1.8' '2']]
我们再对数据进行重组，将原始的4320×24的数据按照每月重组成12个18×480的数据
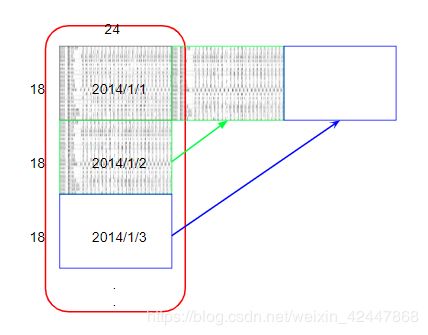
#对data进行调整，将4320*24重组为12*18*480
month_data = {}
for month in range(12):
sample = np.empty([18,480])
for day in range(20):
sample[:,day * 24 : ( day + 1 ) * 24] = raw_data [ 18 * ( 20 * month + day ) : 18 * ( 20 * month + day + 1 ),: ]
month_data[month] = sample
按照作业要求，每9个小时的数据来预测第10个小时的PM2.5，每天24小时，每9个小时构成一个data，第10小时为Label，每天有24-9=15个data和Label，每个月有300个data，所以一年有12×20×15=3600个data
因为1个月20天都是连续的，所以可以将20天的480个小时看成连续的，所以一个月就有480-9=471个data，一年有471×12=5652个data，同样有5652个Label（第10个小时的PM2.5），采用这种方法可以构建较多的data。(每个data中有9×18个数据)
使用如下代码实现:
x = np.empty([12*471,18*9],dtype = float)
y = np.empty([12*471,1],dtype = float)
for month in range(12):
for day in range(20):
for hour in range(24):
if day == 19 and hour>14:
continue
x[month * 471 + day * 24 + hour, :] = month_data[month][:,day * 24 + hour : day * 24 + hour + 9].reshape(1,-1)
y[month * 471 + day * 24 + hour, 0] = month_data[month][9,day * 24 + hour + 9]
print(x)
print(y)
我们可以看一下运行结果，
[[14. 14. 14. ... 2. 2. 0.5]
[14. 14. 13. ... 2. 0.5 0.3]
[14. 13. 12. ... 0.5 0.3 0.8]
...
[17. 18. 19. ... 1.1 1.4 1.3]
[18. 19. 18. ... 1.4 1.3 1.6]
[19. 18. 17. ... 1.3 1.6 1.8]]
[[30.]
[41.]
[44.]
...
[17.]
[24.]
[29.]]
如下图所示，对比train.cxv数据可以看出data和label已经被构建出来
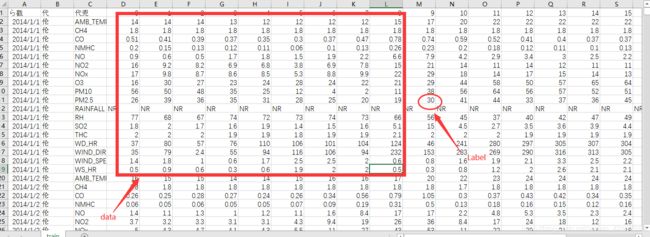对数据进行归一化处理
从训练集中取出一部分设立验证集，目的是为了对模型进行验证
#归一化
mean_x = np.mean(x,axis = 0)
std_x = np.std(x,axis = 0)
for i in range(len(x)):
for j in range(len(x[0])):
if std_x[j] != 0:
x[i][j] = (x[i][j] - mean_x[j]) / std_x[j]
#将训练集分成训练-验证集，用来最后检验我们的模型
x_train_set = x[: math.floor(len(x) * 0.8), :]
y_train_set = y[: math.floor(len(y) * 0.8), :]
x_validation = x[math.floor(len(x) * 0.8): , :]
y_validation = y[math.floor(len(y) * 0.8): , :]
print(x_train_set)
print(y_train_set)
print(x_validation)
print(y_validation)
print(len(x_train_set))
print(len(y_train_set))
print(len(x_validation))
print(len(y_validation))
运行结果
[[-1.35825331 -1.35883937 -1.359222 ... 0.26650729 0.2656797
-1.14082131]
[-1.35825331 -1.35883937 -1.51819928 ... 0.26650729 -1.13963133
-1.32832904]
[-1.35825331 -1.51789368 -1.67717656 ... -1.13923451 -1.32700613
-0.85955971]
...
[ 0.86929969 0.70886668 0.38952809 ... 1.39110073 0.2656797
-0.39079039]
[ 0.71018876 0.39075806 0.07157353 ... 0.26650729 -0.39013211
-0.39079039]
[ 0.3919669 0.07264944 0.07157353 ... -0.38950555 -0.39013211
-0.85955971]]
[[30.]
[41.]
[44.]
...
[ 7.]
[ 5.]
[14.]]
[[ 0.07374504 0.07264944 0.07157353 ... -0.38950555 -0.85856912
-0.57829812]
[ 0.07374504 0.07264944 0.23055081 ... -0.85808615 -0.57750692
0.54674825]
[ 0.07374504 0.23170375 0.23055081 ... -0.57693779 0.54674191
-0.1095288 ]
...
[-0.88092053 -0.72262212 -0.56433559 ... -0.57693779 -0.29644471
-0.39079039]
[-0.7218096 -0.56356781 -0.72331287 ... -0.29578943 -0.39013211
-0.1095288 ]
[-0.56269867 -0.72262212 -0.88229015 ... -0.38950555 -0.10906991
0.07797893]]
[[13.]
[24.]
[22.]
...
[17.]
[24.]
[29.]]
4521
4521
1131
1131
Training：
- 设置超参数：学习率，迭代次数等
- 计算损失L
- 计算梯度gradient
- 梯度下降
损失函数采用均方根误差公式
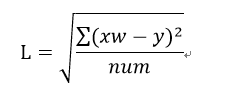
对参数W计算梯度值
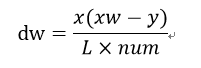
梯度下降，采用RMSprop(指数加权移动平均数)，不理解下面公式的同学百度一下
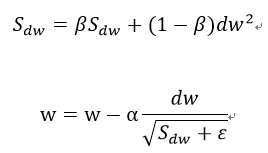
这里原文好像忽略了上一次迭代计算的梯度值（好像会出现梯度消失，不知道为啥），直接用本次迭代的梯度值平方来进行优化
这里就是adagrad方法，原理图在末尾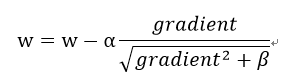 
代码实现如下：
#因为存在偏差bias，所以dim+1
dim = 18 * 9 + 1
# w维度为163*1
w = np.zeros([dim,1])
# x_train_set维度为 4521*163
x_train_set= np.concatenate((np.ones([len(x_train_set),1]),x_train_set),axis = 1).astype(float)
#设置学习率
learning_rate = 10
#设置迭代数
iter_time = 30000
#RMSprop参数初始化
adagrad = np.zeros([dim,1])
eps = 0.0000000001
#beta = 0.9
#迭代
for t in range(iter_time):
loss = np.sqrt(np.sum(np.power(np.dot(x_train_set,w)-y_train_set,2))/len(x_train_set))
if(t%100 == 0):
print("迭代的次数：%i ， 损失值：%f"%(t,loss))
#gradient = 2*np.dot(x.transpose(),np.dot(x,w)-y)
#计算梯度值
gradient = (np.dot(x_train_set.transpose(),np.dot(x_train_set,w)-y_train_set))/(loss*len(x_train_set))
adagrad += (gradient ** 2)
#更新参数w
w = w - learning_rate * gradient / np.sqrt(adagrad + eps)
#保存参数w
np.save('weight.npy',w)
我们看看运行结果，这里我只贴了部分打印值，迭代30000次损失值收敛到了19，epoch可以自己设置试试看
发现损失值出现波动，但好消息是逐渐在收敛，好像用RMSprop优化会出现这种情况
如果你用第一个gradient计算梯度好像没有波动出现，可以试试看
迭代的次数：0 ， 损失值：27.239592
迭代的次数：100 ， 损失值：598.991742
迭代的次数：200 ， 损失值：96.973083
迭代的次数：300 ， 损失值：240.807182
迭代的次数：400 ， 损失值：71.607934
迭代的次数：500 ， 损失值：212.116933
迭代的次数：600 ， 损失值：117.461546
迭代的次数：700 ， 损失值：189.660439
迭代的次数：800 ， 损失值：87.943008
迭代的次数：900 ， 损失值：158.851111
迭代的次数：1000 ， 损失值：74.318934
迭代的次数：1100 ， 损失值：138.784655
迭代的次数：1200 ， 损失值：67.418347
迭代的次数：1300 ， 损失值：124.302389
迭代的次数：1400 ， 损失值：63.235512
迭代的次数：1500 ， 损失值：113.160475
迭代的次数：1600 ， 损失值：60.299076
到这里为止，模型已经训练好了，我们在验证集上验证一下模型，并对测试集test.cxv进行预测
先对测试集test.csv进行预处理
testdata = pd.read_csv('E:/jupyter/data/hw1/test.csv',header = None ,encoding = 'big5')
test_data = testdata.iloc[:,2:]
test_data[test_data == 'NR'] = 0
test_data = test_data.to_numpy()
test_x = np.empty([240,18*9],dtype = float)
for i in range(240):
test_x[i,:] = test_data[18*i:18*(i+1),:].reshape(1,-1)
for i in range(len(test_x)):
for j in range(len(test_x[0])):
if std_x[j] != 0:
test_x[i][j] = (test_x[i][j] - mean_x[j]) / std_x[j]
test_x = np.concatenate((np.ones([240,1]),test_x),axis = 1).astype(float)
print(test_x)
看看运行结果
array([[ 1. , -0.24447681, -0.24545919, ..., -0.67065391,
-1.04594393, 0.07797893],
[ 1. , -1.35825331, -1.51789368, ..., 0.17279117,
-0.10906991, -0.48454426],
[ 1. , 1.5057434 , 1.34508393, ..., -1.32666675,
-1.04594393, -0.57829812],
...,
[ 1. , 0.3919669 , 0.54981237, ..., 0.26650729,
-0.20275731, 1.20302531],
[ 1. , -1.8355861 , -1.8360023 , ..., -1.04551839,
-1.13963133, -1.14082131],
[ 1. , -1.35825331, -1.35883937, ..., 2.98427476,
3.26367657, 1.76554849]])
验证模型并预测
#在验证集上进行验证
w = np.load('weight.npy')
x_validation= np.concatenate((np.ones([len(x_validation),1]),x_validation),axis = 1).astype(float)
for m in range(len(x_validation)):
Loss = np.sqrt(np.sum(np.power(np.dot(x_validation,w)-y_validation,2))/len(x_validation))
print ("the Loss on val data is %f" % (Loss))
#预测
ans_y = np.dot(test_x, w)
print('预测PM2.5值')
print(ans_y)
运行结果
the Loss on val data is 18.427185
预测PM2.5值
[[-15.78367116]
[ -2.32261409]
[ 59.74234153]
[ -2.69635112]
[ 39.23820506]
[ 13.8801302 ]
[ 22.58641017]
[ 31.11258594]
[ 41.92474119]
[ 68.36693984]
[ 17.54723298]
[ 42.69150518]
[ 85.92726242]
[ 64.53572169]
[ 26.60792925]
[ -7.59077676]
可以看出，在我们设立的验证集上，误差为18.4，并且在测试集上有些预测值为负值，所以模型还是存在较大误差，有待优化。
注：运行过程中出现维度不匹配情况时，从头运行一下程序便可。
有错误的地方希望大家批评指正，谢谢！
梯度下降的地方理解有误：刚看了Gradient Descent1的视频，adagrad方法如下图所示
