微积分由来详解
本文参考:https://www.zhihu.com/question/336322284/answer/918067537
1.求曲线面积
求图形面积这么多,不可能每次都记得公式,况且很多都还没有公式。
所以,人们想到一种穷竭法:用n个矩形去逼近这个图形。
2.初见积分
面积就是无穷小量dx(宽)×函数值(纵坐标/高)
3.直线和斜率
直线的斜率就是表明直接的倾斜程度的,纵坐标之差Δy和横坐标之差Δx的比值(Δy/Δx)来定义这条直线斜率。
4.曲线和切线
而曲线每个点的斜率都是不一样的,所以不同的点有者不同的倾斜程度。
而曲线每个点的倾斜程度就是该点切线的斜率。
切线就是一条经过曲线某个点且与曲线只有一个交点的直线。
5.初见微分
而切线是当曲线上A、B两点相隔无穷小时确定的直线,那么切线的斜率依然可以写成Δy/Δx,只不过这时Δx和Δy都无限趋近于0。莱布尼茨就给这两个趋近于0却又不等于0的Δx和Δy重新取了一个名字:dx和dy,并把它们称为“微分”。
6.导数
原函数微分就是导数。
曲线上的任何一点都有个斜率(切线对应的倾斜程度),所以一个点和一个斜率对应,而斜率通过微分求得,显然微分后也是一个函数,一一对应,这个就是导函数,简称导数。
7.导数的意义
这个就是微分学的核心了。
因为导数反映的是一个量变化快慢的程度,这其实就是一种广义的“速度”。
所以我们可以知道一个函数的增长快慢,当为0的时候就停止增长/减少,此时我们可以来求极大极小值。
8.互逆运算
积分与微分是一对互逆运算。
求面积(积分)和求导(微分)是一对互逆运算”的时候,那就是说如果有一个东西,我们对它进行积分操作(求面积)可以得到一个新东西,如果我们对这个新东西再进行微分操作(求导)又能得到原来的那个东西,这样才算互逆。
例子:物理中的速度曲线(速度与位移的关系):
处理曲线的时候,我们把时间切成很多块,用每一个小块的面积(位移)之和去逼近总面积(位移),这不就是积分的思想么?反过来,如果你把这个黄色的面积S,把这个整体的位移看作一个随时间t变化的函数,对它求导自然就能得到速度v。也就是说,我们对速度v做一次积分能得到位移s;反过来,对位移s求一次导数(微分)就能得到速度v。这样它们的互逆关系就非常清楚了
9.原函数(互逆运算的作用)
在前面我们看到:算积分(函数与x轴围成的面积的时候),我们用的是矩形穷竭法,很明显缺点很多(1.面对不同的曲线有着不同的公式(因为我们要按照n个矩形长×宽来算)2.要舍去后面的无穷小项)
这里拿物理中的速度v与位移s举例:
我们很明显知道s对t求导就是v,而我们现在问题是要通过v得到s,且v是由s对t求导而来的,那么就做对v做逆微分运算呗,当我们知道f(x)=2x的时候,我们肯定知道f(x)是由哪个原函数微分而来的:g(x)=x2,这就是我们一开始写的用积分符号对f(x)求积分其实就是在对f(x)求逆微分运算。
所以整个逻辑是这样的:
- 积分:v求s(但是只有缺点明显的穷竭法),微分:s求出v
- 发现积分和微分互为逆运算
- 那用穷竭的积分不行,我们就用微分,对v采取逆微分运算**,而这里的逆微分就是我们后来广义讨论的积分**。
10.微积分基本定理
既然要用反向微分的方法求面积,那我们就去找f(x)=x²的原函数g(x),而g(x)的意义是负无穷到x,函数f(x)围成的面积,所以f(x)从0~1围成的面积就是:g(1)-g(0)。
微积分基本定理(牛顿-莱布尼茨公式)就非常容易理解了:如果函数f(x)在区间a到b之间连续(简单理解就是曲线没有断),并且存在原函数F(x),那么就有:

微积分之所以能够简化求面积的逻辑,是因为微积分把这块逻辑都打包到求原函数里去了,而后者是一个可以程序化、一般化的操作,而不是用各种图形去竭尽,这样很麻烦。
-因为给f(x)直接求g(x)很麻烦,但g(x)->f(x)简单,那就逆过来操作。就像在鸡兔同笼里,告诉鸡兔的数量求头和脚数量easy,但反过来就麻烦,那么依然用前者思路,将鸡兔数量设出,表示成头和脚的数量。
11.被忽略的无穷小
前文说到的微积分,虽然积分是可以是逆微分,但是微分中也忽略了无穷小dx,只是直观地认为可以忽略且不为0。
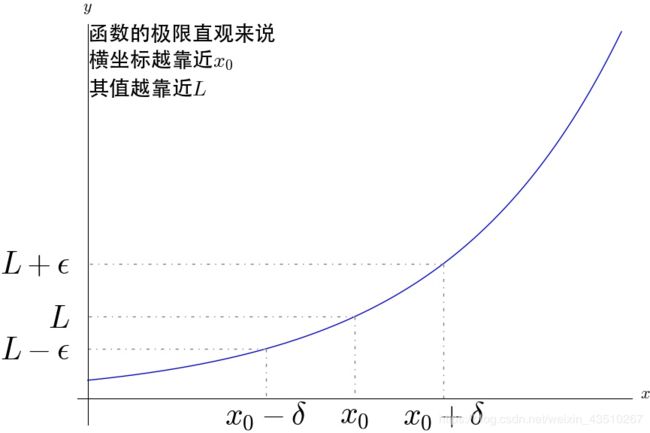
这里我把柯西对极限的新定义:当一个变量相继的值无限地趋近某个固定值的时候,如果它同这个固定值之间的差可以随意地小,那么这个固定值就被称为它的极限。
可以随意的小和你主动去无限逼近是完全不一样的。可以随意小的意思是:你让我多小我就可以多小。你让我小于0.1,我就能小于0.1;你让我小于0.01,我就能小于0.01;你让我小于0.00…001,我就可以小于0.00…001。只要你能说出一个确定的值,不管你说的值有多小,我都可以让它跟这个固定值的差比你更小。柯西说如果这样的话,那么这个固定值就是它的极限。
无穷小量:一个“只要你可以说出一个数,我肯定就可以让我和0之间的差比你给的数更小”的量。
12.魏尔斯特拉斯和ε-δ极限
根据柯西的思想,魏尔斯特拉斯说:你要判断某个函数f(x)在某个地方a的极限是不是某个值L,关键就要看如果我任意说一个数ε(比如0.00…001或者任意其它的,注意是任意取,这里用ε代替),你能不能找到一个x的取值范围(用δ来衡量),让这个范围里的函数值f(x)与那个值L之间的差(用套个绝对值的|f(x)-L|表示)小于ε。如果你总能找到这样的δ,那我就说函数f(x)在a点的极限为L。用精练的数学语言表述上面的话就是:当且仅当对于任意的ε,存在一个δ>0,使得只要0<|x-a|<δ,就有|f(x)-L|<ε,那么我们就说f(x)在a点的极限为L。记做:
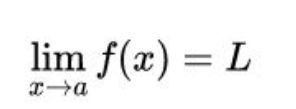
13.导数的重建
很显然,这个定义是依赖无穷小量的,我们现在要用ε-δ定义的极限来代替这个无穷小量。所以,切线就应该被理解为割线的极限,那么切线的斜率(也就是这点的导数)自然就是割线斜率的极限,所以导数f(x)’也自然而然地成了一个极限。
由于割线的斜率就是用这两点的纵坐标之差f(x+Δx)-f(x)除以这两点的横坐标之差(x+Δx-x=Δx),而导数f(x)’是割线斜率的极限。那么,我们在割线斜率的前面加一个极限符号就可以表示导数f(x)’了:

这才是导数的真正定义,它是一个极限,而不再是两个无穷小量dy与dx的商dy/dx。也就是说,按照极限的ε-δ定义,这个导数f(x)’的真正含义是:你任意给一个ε,我都能让割线的斜率与这个值的差比你给的ε更小。
14.微分的重建
我们今天仍然用dy/dx表示导数,但是大家一定要注意,dy/dx在现代语境里是一个极限,不再是两个无穷小量的商。
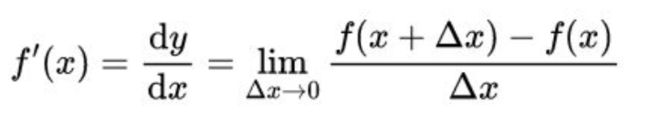
这个dx和dy还是有意义的,当然,有意义也肯定不可能再是以前无穷小量的意思了。那么,在ε-δ极限这种全新的语境下,dx和dy在新时代的意义又是什么呢?
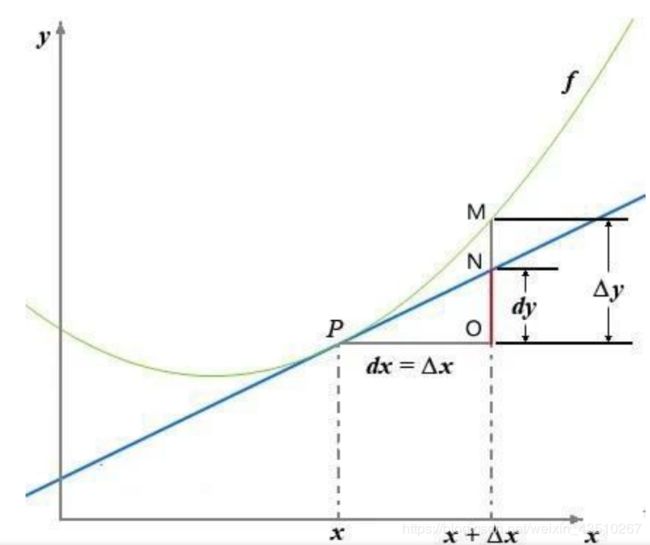
当自变量变化了Δx的时候,Δy表示实际的曲线的变化量,而微分dy则表示这条切线上的变化量,这就是新的语境下函数微分dy的含义。而自变量的微分dx,大家可以看到,就跟x轴的变化量Δx是一回事。
dy和Δx之间就存在这样一种线性关系:dy=A·Δx。
微分的严格定义是这样的:对于Δy是否存在着一个关于Δx为线性的无穷小A·Δx(A为常数),使它与Δy的差是较Δx更高阶的无穷小。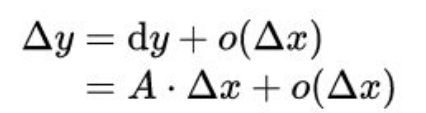
如果这个式子成立,我们就说函数y=f(x)在这点是可微的,dy=A·Δx就是函数的微分。因为这是一个线性函数,所以我们说微分dy是Δy的线性主部。