优化问题 | 约束优化问题的KKT条件、拉格朗日对偶法、内外点罚函数法
文章目录
- 1 KKT条件
- 1.1 什么是KKT条件
- 1.2 等式约束优化问题(Lagrange乘数法)
- 1.3 不等式约束优化问题
- 2 拉格朗日对偶法
- 2.1 原始问题
- 2.2 对偶问题
- 2.3 原始问题与对偶问题的关系
- 2.4 对偶上升法
- 2.5 对偶分解法
- 3 内外点罚函数法
- 3.1 外点罚函数法
- 3.2 内点罚函数法
- 4 参考资料
1 KKT条件
1.1 什么是KKT条件
对于具有等式和不等式约束的一般优化问题 m i n f ( x ) s . t . g j ( x ) ≤ 0 ( j = 1 , 2 , … , l ) h k ( x ) = 0 ( k = 1 , 2 , … , m ) \begin{aligned}&minf(\bold x) \\ &s.t.\;g_j(\bold x)\leq0(j=1,2,\dots ,l)\\&\;\;\;\;\;\;h_k(\bold x)=0(k=1,2,\dots ,m)\end{aligned} minf(x)s.t.gj(x)≤0(j=1,2,…,l)hk(x)=0(k=1,2,…,m)
KKT条件(Karush-Kuhn-Tucker conditions)给出了判断 x ∗ \bold x^* x∗是否为最优解的必要条件
∂ f ∂ x i + ∑ j = 1 m μ j ∂ g j ∂ x i + ∑ k = 1 l λ k ∂ h k ∂ x i = 0 ( i = 1 , 2 , … , n ) h k ( x ) = 0 ( k = 1 , 2 , … , l ) μ j g j ( x ) = 0 ( j = 1 , 2 , … , m ) μ j ≥ 0 \begin{aligned}&\frac{\partial f}{\partial x_i}+\sum_{j=1}^m\mu_j\frac{\partial g_j}{\partial x_i}+\sum_{k=1}^l\lambda_k\frac{\partial h_k}{\partial x_i}=0(i=1,2,\dots ,n)\\ &h_k(\bold x)=0(k=1,2,\dots ,l)\\&\mu_jg_j(\bold x)=0(j=1,2,\dots ,m)\\&\mu_j\geq 0\end{aligned} ∂xi∂f+j=1∑mμj∂xi∂gj+k=1∑lλk∂xi∂hk=0(i=1,2,…,n)hk(x)=0(k=1,2,…,l)μjgj(x)=0(j=1,2,…,m)μj≥0
1.2 等式约束优化问题(Lagrange乘数法)
等式约束优化问题 m i n f ( x 1 , x 2 , … , x n ) s . t . h k ( x 1 , x 2 , … , x n ) = 0 ( k = 1 , 2 , … , m ) \begin{aligned}&minf(x_1,x_2,\dots ,x_n) \\ &s.t.\;h_k(x_1,x_2,\dots ,x_n)=0(k=1,2,\dots ,m)\end{aligned} minf(x1,x2,…,xn)s.t.hk(x1,x2,…,xn)=0(k=1,2,…,m)Lagrange函数 L ( x , λ ) = f ( x ) + ∑ k = 1 k λ k h k ( x ) L(\bold x,\lambda)=f(\bold x)+\sum_{k=1}^k\lambda_kh_k(\bold x) L(x,λ)=f(x)+k=1∑kλkhk(x)其中 λ \lambda λ为Lagrange乘子
等式约束的极值必要条件: ∂ L ∂ x i = 0 ( i = 1 , 2 , … , n ) ∂ L ∂ λ k = 0 ( k = 1 , 2 , … , m ) \begin{aligned}&\frac{\partial L}{\partial x_i}=0(i=1,2,\dots ,n)\\ &\frac{\partial L}{\partial \lambda_k}=0(k=1,2,\dots ,m)\end{aligned} ∂xi∂L=0(i=1,2,…,n)∂λk∂L=0(k=1,2,…,m)
理解:
在无约束优化问题 m i n f ( x 1 , x 2 , … , x n ) minf(x_1,x_2,\dots ,x_n) minf(x1,x2,…,xn)中, x i x_i xi为优化变量,我们根据极值的必要条件 ∂ f ∂ x i = 0 \frac{\partial f}{\partial x_i}=0 ∂xi∂f=0求出可能的极值点;
在等式约束优化问题中,Lagrange乘数法引入了m个Lagrange乘子,我们可以把 λ k \lambda_k λk也看作优化变量,相当于优化变量个数从n增加到n+m个,均对它们求偏导。
1.3 不等式约束优化问题
- 主要思想:转化——将不等式约束条件变成等式约束条件
- 具体做法:引入松弛变量,松弛变量也是优化变量,也需要一视同仁求偏导
以一元函数为例, m i n f ( x ) s . t . g 1 ( x ) = a − x ≤ 0 g 2 ( x ) = x − b ≤ 0 \begin{aligned}&minf(x) \\ &s.t.\;g_1(x)=a-x\leq 0\\&\;\;\;\;\;\;g_2(x)=x-b\leq 0\end{aligned} minf(x)s.t.g1(x)=a−x≤0g2(x)=x−b≤0
对于约束 g 1 g_1 g1和 g 2 g_2 g2,我们引入两个松弛变量 a 1 2 a_1^2 a12和 b 1 2 b_1^2 b12,得到
h 1 ( x ) = g 1 ( x ) + a 1 2 = a − x + a 1 2 = 0 h 2 ( x ) = g 2 ( x ) + b 1 2 = x − b + a 1 2 = 0 \begin{aligned}&h_1(x)=g_1(x)+a_1^2=a-x+a_1^2=0\\ &h_2(x)=g_2(x)+b_1^2=x-b+a_1^2=0\end{aligned} h1(x)=g1(x)+a12=a−x+a12=0h2(x)=g2(x)+b12=x−b+a12=0取平方项而非 a 1 , b 1 a_1,b_1 a1,b1是因为 g 1 g_1 g1和 g 2 g_2 g2必须加上一个非负数才能变为等式,若取后者还需加限制条件 a 1 ≥ 0 , b 1 ≥ 0 a_1\geq 0,b_1\geq 0 a1≥0,b1≥0,使问题更复杂
由此我们将不等式约束转为等式约束,新的Lagrange函数为 L ( x , a 1 , b 1 , μ 1 , μ 2 ) = f ( x ) + μ 1 ( a − x + a 1 2 ) + μ 2 ( x − b + b 1 2 ) L(x,a_1,b_1,\mu_1,\mu_2)=f(x)+\mu_1(a-x+a_1^2)+\mu_2(x-b+b_1^2) L(x,a1,b1,μ1,μ2)=f(x)+μ1(a−x+a12)+μ2(x−b+b12)按照等式约束条件对其求解,得联立方程 ∂ L ∂ x = ∂ f ∂ x + μ 1 ∂ g 1 ∂ x + μ 2 ∂ g 2 ∂ x = 0 ∂ L ∂ μ 1 = g 1 + a 1 2 = 0 , ∂ L ∂ μ 2 = g 2 + b 1 2 = 0 ∂ L ∂ a 1 = 2 μ 1 a 1 = 0 , ∂ L ∂ b 1 = 2 μ 2 b 1 = 0 μ 1 ≥ 0 , μ 2 ≥ 0 \begin{aligned}&\frac{\partial L}{\partial x}=\frac{\partial f}{\partial x}+\mu_1\frac{\partial g_1}{\partial x}+\mu_2\frac{\partial g_2}{\partial x}=0\\&\frac{\partial L}{\partial \mu_1}=g_1+a_1^2=0,\frac{\partial L}{\partial \mu_2}=g_2+b_1^2=0\\&\frac{\partial L}{\partial a_1}=2\mu_1a_1=0,\frac{\partial L}{\partial b_1}=2\mu_2b_1=0\\&\mu_1\geq 0,\mu_2\geq 0\end{aligned} ∂x∂L=∂x∂f+μ1∂x∂g1+μ2∂x∂g2=0∂μ1∂L=g1+a12=0,∂μ2∂L=g2+b12=0∂a1∂L=2μ1a1=0,∂b1∂L=2μ2b1=0μ1≥0,μ2≥0
利用第二行和第三行的四个式子,针对 2 μ 1 a 1 = 0 2\mu_1a_1=0 2μ1a1=0,我们可得到如下两种情形:
- 情形一: a 1 ≠ 0 a_1\neq 0 a1=0,则有 μ 1 = 0 \mu_1=0 μ1=0,约束 g 1 g_1 g1不起作用,且有 g 1 < 0 g_1<0 g1<0
- 情形二: a 1 = 0 a_1=0 a1=0,则有 μ 1 ≥ 0 \mu_1\geq 0 μ1≥0,约束 g 1 g_1 g1起作用,且有 g 1 = 0 g_1=0 g1=0
合并两种情形,有 μ 1 g 1 = 0 \mu_1g_1=0 μ1g1=0,约束起作用时, μ 1 ≥ 0 \mu_1\geq 0 μ1≥0, g 1 = 0 g_1=0 g1=0,约束不起作用时, μ 1 = 0 \mu_1=0 μ1=0, g 1 < 0 g_1<0 g1<0;
2 μ 2 b 1 = 0 2\mu_2b_1=0 2μ2b1=0同理;
由此,必要条件转化为 ∂ f ∂ x + μ 1 ∂ g 1 ∂ x + μ 2 ∂ g 2 ∂ x = 0 μ 1 g 1 ( x ) = 0 , μ 2 g 2 ( x ) = 0 μ 1 ≥ 0 , μ 2 ≥ 0 \begin{aligned}&\frac{\partial f}{\partial x}+\mu_1\frac{\partial g_1}{\partial x}+\mu_2\frac{\partial g_2}{\partial x}=0\\&\mu_1g_1(x)=0,\mu_2g_2(x)=0\\&\mu_1\geq 0,\mu_2\geq 0\end{aligned} ∂x∂f+μ1∂x∂g1+μ2∂x∂g2=0μ1g1(x)=0,μ2g2(x)=0μ1≥0,μ2≥0
针对多元的情况,则有 ∂ f ( x ) ∂ x i + ∑ j = 1 m μ j ∂ g j ( x ) ∂ x = 0 ( i = 1 , 2 , … , n ) μ j g j ( x ) = 0 ( j = 1 , 2 , … , m ) μ j ≥ 0 ( j = 1 , 2 , … , m ) \begin{aligned}&\frac{\partial f(x)}{\partial x_i}+\sum_{j=1}^m\mu_j\frac{\partial g_j(x)}{\partial x}=0(i=1,2,\dots ,n)\\&\mu_jg_j(x)=0(j=1,2,\dots ,m)\\&\mu_j\geq 0(j=1,2,\dots ,m)\end{aligned} ∂xi∂f(x)+j=1∑mμj∂x∂gj(x)=0(i=1,2,…,n)μjgj(x)=0(j=1,2,…,m)μj≥0(j=1,2,…,m)上式即为不等式优化问题的KKT条件, μ j \mu_j μj为KKT乘子,约束起作用时, μ j ≥ 0 \mu_j\geq 0 μj≥0, g j = 0 g_j=0 gj=0,约束不起作用时, μ j = 0 \mu_j=0 μj=0, g j < 0 g_j<0 gj<0
KKT乘子必须大于等于0
由于 ∂ f ( x ) ∂ x i + ∑ j = 1 m μ j ∂ g j ( x ) ∂ x = 0 ( i = 1 , 2 , … , n ) \frac{\partial f(x)}{\partial x_i}+\sum_{j=1}^m\mu_j\frac{\partial g_j(x)}{\partial x}=0(i=1,2,\dots ,n) ∂xi∂f(x)+∑j=1mμj∂x∂gj(x)=0(i=1,2,…,n),写成梯度形式有 ∇ f ( x ) + ∑ j ∈ J μ j ∇ g j ( x ) = 0 \nabla f(x)+\sum_{j\in J}\mu_j\nabla g_j(x)=0 ∇f(x)+j∈J∑μj∇gj(x)=0J为起约束作用的集合,移项得 − ∇ f ( x ) = ∑ j ∈ J μ j ∇ g j ( x ) -\nabla f(x)=\sum_{j\in J}\mu_j\nabla g_j(x) −∇f(x)=j∈J∑μj∇gj(x)注意到梯度为向量,上式表明在约束极小值点处, f ( x ) f(x) f(x)的梯度一定可以表示成所有起作用的约束在该点的梯度的线性组合
假设只有两个起作用约束,且约束起作用时 g j ( x ) = 0 g_j(\bold x)=0 gj(x)=0,此时约束在几何上是一簇约束平面,我们假设在 x k x^k xk处取极小值,则 x k x^k xk一定在这两个平面的交线上,且 − ∇ f ( x k ) , ∇ g 1 ( x k ) , ∇ g 2 ( x k ) -\nabla f(x^k),\nabla g_1(x^k),\nabla g_2(x^k) −∇f(xk),∇g1(xk),∇g2(xk)共面
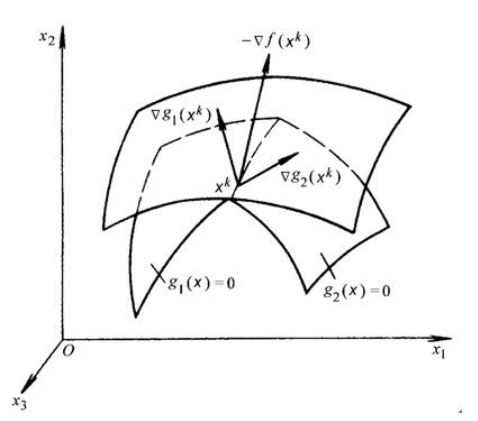
在点 x k x^k xk处沿 x 1 O x 2 x_1Ox_2 x1Ox2平面的截图如下,有两种情况:
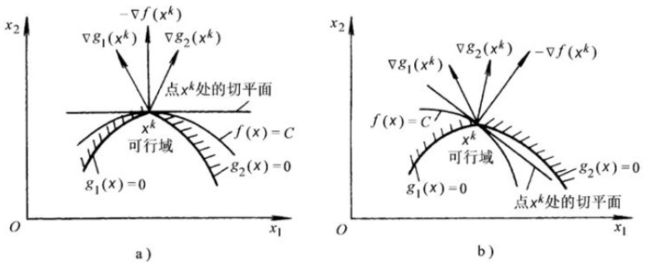
若 − ∇ f -\nabla f −∇f落在 ∇ g 1 \nabla g_1 ∇g1和 ∇ g 2 \nabla g_2 ∇g2所形成的的锥角区外的一侧,如情形b,作等值面 f ( x ) = C f(\bold x)=C f(x)=C在点 x k \bold x^k xk的切平面(与 − ∇ f -\nabla f −∇f垂直),我们发现,沿着与负梯度 − ∇ f -\nabla f −∇f成锐角的方向移动, f ( x ) f(\bold x) f(x)总能减小,因此 x k \bold x^k xk仍可沿约束曲面移动,既可减小目标函数值,又不破坏约束条件,所以 x k \bold x^k xk不是局部极值点
若 − ∇ f -\nabla f −∇f落在 ∇ g 1 \nabla g_1 ∇g1和 ∇ g 2 \nabla g_2 ∇g2所形成的的锥角内,如情形a,同样作等值面 f ( x ) = C f(\bold x)=C f(x)=C在点 x k \bold x^k xk的切平面(与 − ∇ f -\nabla f −∇f垂直),沿着与负梯度 − ∇ f -\nabla f −∇f成锐角的方向移动,虽然能使目标函数值减小,但此时任何一点都不在可行区域内,所以此时 x k \bold x^k xk就是局部极值点
由于 − ∇ f -\nabla f −∇f和 ∇ g 1 , ∇ g 2 \nabla g_1,\nabla g_2 ∇g1,∇g2在一个平面内,所以前者可以看成是后两者的线性组合,又 − ∇ f -\nabla f −∇f落在 ∇ g 1 \nabla g_1 ∇g1和 ∇ g 2 \nabla g_2 ∇g2所形成的的锥角内,所以线性组合的系数为正,有 − ∇ f ( x k ) = μ 1 ∇ g 1 ( x ∗ ) + μ 2 ∇ g 2 ( x ∗ ) , 且 μ 1 > 0 , μ 2 > 0 -\nabla f(\bold x^k)=\mu_1\nabla g_1(\bold x^*)+\mu_2\nabla g_2(\bold x^*),且\mu_1>0,\mu_2>0 −∇f(xk)=μ1∇g1(x∗)+μ2∇g2(x∗),且μ1>0,μ2>0
类似地,当有多个不等式约束起作用时,要求 − ∇ f -\nabla f −∇f落在 ∇ g j \nabla g_j ∇gj形成的超角锥内。
2 拉格朗日对偶法
在约束最优化问题中,常常利用拉格朗日对偶性(Lagrange duality)将原始问题转化为对偶问题,通过求解对偶问题得到原始问题的解。
2.1 原始问题
假设 f ( x ) , g i ( x ) , h j ( x ) f(x),g_i(x),h_j(x) f(x),gi(x),hj(x)为连续可微函数,以下约束最优化问题称为原始问题 m i n f ( x ) s . t . g j ( x ) ≤ 0 ( j = 1 , 2 , … , l ) h k ( x ) = 0 ( k = 1 , 2 , … , m ) \begin{aligned}&minf(x) \\ &s.t.\;g_j(x)\leq0(j=1,2,\dots ,l)\\&\;\;\;\;\;\;h_k(x)=0(k=1,2,\dots ,m)\end{aligned} minf(x)s.t.gj(x)≤0(j=1,2,…,l)hk(x)=0(k=1,2,…,m)引进广义拉格朗日函数(generalized Lagrange function) L ( x , μ , λ ) = f ( x ) + ∑ j = 1 l μ j g j ( x ) + ∑ k = 1 m λ k h k ( x ) L(x,\mu,\lambda)=f(x)+\sum_{j=1}^l\mu_jg_j(x)+\sum_{k=1}^m\lambda_kh_k(x) L(x,μ,λ)=f(x)+j=1∑lμjgj(x)+k=1∑mλkhk(x)考虑x的函数 θ P ( x ) = m a x μ , λ , μ i ≥ 0 L ( x , μ , λ ) \theta_P(x)=\underset{\mu,\lambda,\mu_i\geq0}{max}L(x,\mu,\lambda) θP(x)=μ,λ,μi≥0maxL(x,μ,λ)其中下标P表示原始问题
假设给定某个x,
- 如果x违反原始问题的约束条件,则 θ P ( x ) = + ∞ \theta_P(x)=+\infty θP(x)=+∞
- 若存在某个j使得 g j ( x ) > 0 g_j(x)>0 gj(x)>0,则可令 μ j → + ∞ \mu_j\rightarrow+\infty μj→+∞,其余 μ j , λ k \mu_j,\lambda_k μj,λk均为0
- 存在某个k使得 h k ( x ) ≠ 0 h_k(x)\neq 0 hk(x)=0,则可令 β j \beta_j βj满足 β j h j ( x ) → + ∞ \beta_jh_j(x)\rightarrow+\infty βjhj(x)→+∞,其余 μ j , λ k \mu_j,\lambda_k μj,λk均为0
- 如果x满足原始问题的约束条件,则 θ P ( x ) = f ( x ) \theta_P(x)=f(x) θP(x)=f(x)
因此 θ P ( x ) = { f ( x ) , x 满 足 原 始 问 题 约 束 + ∞ , 其 他 \theta_P(x)=\left\{\begin{array}{l}f(x),x\mathrm{满足原始问题约束}\\+\infty,\mathrm{其他}\end{array}\right. θP(x)={f(x),x满足原始问题约束+∞,其他
考虑极小化问题 m i n x θ P ( x ) = m i n x m a x μ , λ , μ i ≥ 0 L ( x , μ , λ ) \underset{x}{min}\theta_P(x)=\underset{x}{min}\underset{\mu,\lambda,\mu_i\geq0}{max}L(x,\mu,\lambda) xminθP(x)=xminμ,λ,μi≥0maxL(x,μ,λ)它与原始最优化问题等价,即它们有相同的解,问题 m i n x m a x μ , λ , μ i ≥ 0 L ( x , μ , λ ) \underset{x}{min}\underset{\mu,\lambda,\mu_i\geq0}{max}L(x,\mu,\lambda) xminμ,λ,μi≥0maxL(x,μ,λ)称为广义拉格朗日函数的极小极大问题。
定义原始问题的最优值为原始问题的解: p ∗ = m i n x θ P ( x ) p^*=\underset{x}{min}\theta_P(x) p∗=xminθP(x)
2.2 对偶问题
定义 θ D ( μ , λ ) = m i n x L ( x , μ , λ ) \theta_D(\mu,\lambda)=\underset{x}{min}L(x,\mu,\lambda) θD(μ,λ)=xminL(x,μ,λ)再考虑极大化 θ D ( μ , λ ) \theta_D(\mu,\lambda) θD(μ,λ) m a x μ , λ , μ i ≥ 0 θ D ( μ , λ ) = m a x μ , λ , μ i ≥ 0 m i n x L ( x , μ , λ ) \underset{\mu,\lambda,\mu_i\geq0}{max}\theta_D(\mu,\lambda)=\underset{\mu,\lambda,\mu_i\geq0}{max}\underset{x}{min}L(x,\mu,\lambda) μ,λ,μi≥0maxθD(μ,λ)=μ,λ,μi≥0maxxminL(x,μ,λ)问题 m a x μ , λ , μ i ≥ 0 m i n x L ( x , μ , λ ) \underset{\mu,\lambda,\mu_i\geq0}{max}\underset{x}{min}L(x,\mu,\lambda) μ,λ,μi≥0maxxminL(x,μ,λ)称为拉格朗日函数的极大极小问题
以下约束最优化问题称为原始问题的对偶问题 m a x μ , λ θ D ( μ , λ ) = m a x μ , λ m i n x L ( x , μ , λ ) s . t . μ i ≥ 0 , i = 1 , 2 , … , l \begin{aligned}&\underset{\mu,\lambda}{max}\theta_D(\mu,\lambda)=\underset{\mu,\lambda}{max}\;\underset{x}{min}L(x,\mu,\lambda)\\&s.t. \mu_i\geq0,i=1,2,\dots ,l\end{aligned} μ,λmaxθD(μ,λ)=μ,λmaxxminL(x,μ,λ)s.t.μi≥0,i=1,2,…,l定义对偶问题的最优值为对偶问题的值 d ∗ = m a x μ , λ , μ i ≥ 0 θ D ( μ , λ ) d^*=\underset{\mu,\lambda,\mu_i\geq0}{max}\theta_D(\mu,\lambda) d∗=μ,λ,μi≥0maxθD(μ,λ)
对偶函数与共轭函数
原 函 数 : f ( x ) : R n → R 共 轭 函 数 : f ∗ ( y ) : R n → R } → f ∗ ( y ) = sup x ∈ d o m f ( y T x − f ( x ) ) \left.\begin{array}{rl}原函数:&{f(x): R^{n} \rightarrow R} \\共轭函数:&{f^{*}(y): R^{n} \rightarrow R}\end{array}\right\} \rightarrow f^{*}(y)=\sup _{x \in \mathrm{dom} f}\left(y^{T} x-f(x)\right) 原函数:共轭函数:f(x):Rn→Rf∗(y):Rn→R}→f∗(y)=x∈domfsup(yTx−f(x))
其中, sup ( g ( x ) ) \sup (g(x)) sup(g(x))表示函数 g ( x ) g(x) g(x)在整个定义域 x ∈ d o m g x\in \mathrm{dom} g x∈domg中的最大值,y则取任意常数或常向量,对每一个y值, f ∗ ( y ) f^*(y) f∗(y)都会对应一个值,将y拓展到整个取值范围后即可得到关于y的函数 f ∗ ( y ) f^*(y) f∗(y),即函数 f ( x ) f(x) f(x)的共轭函数。
考虑线性约束下的最优化问题 min f ( x ) s . t . A x ≤ b , C x = d \begin{array}{l}{\min f(x)} \\ s.t.\;Ax\leq b,Cx=d\end{array} minf(x)s.t.Ax≤b,Cx=d
将其对偶函数凑出共轭函数形式: g ( λ , ν ) = inf x ( f ( x ) + λ T ( A x − b ) + ν T ( C x − d ) ) = − λ T b − ν T d + inf x ( f ( x ) + λ T A x + ν T C x ) = − λ T b − ν T d − sup x ( ( − A T λ − C T ν ) T x − f ( x ) ) = − λ T b − ν T d − f ∗ ( − A T λ − C T ν ) \begin{aligned}g(\lambda, \nu)&=\inf _{x}\left(f(x)+\lambda^{T}(A x-b)+\nu^{T}(C x-d)\right)\\&=-\lambda^{T} b-\nu^{T} d+\inf _{x}\left(f(x)+\lambda^{T} A x+\nu^{T} C x\right) \\&=-\lambda^{T} b-\nu^{T} d-\sup _{x}\left(\left(-A^{T} \lambda-C^{T} \nu\right)^{T} x-f(x)\right) \\&=-\lambda^{T} b-\nu^{T} d-f^{*}\left(-A^{T} \lambda-C^{T} \nu\right)\end{aligned} g(λ,ν)=xinf(f(x)+λT(Ax−b)+νT(Cx−d))=−λTb−νTd+xinf(f(x)+λTAx+νTCx)=−λTb−νTd−xsup((−ATλ−CTν)Tx−f(x))=−λTb−νTd−f∗(−ATλ−CTν)
即线性约束下的对偶函数可以用共轭函数表示,其自变量为拉格朗日乘子的线性组合。
2.3 原始问题与对偶问题的关系
定理1(弱对偶性: d ∗ ≤ p ∗ d^*\leq p^* d∗≤p∗)
若原始问题和对偶问题都有最优值,则 d ∗ = m a x μ , λ , μ i ≥ 0 m i n x L ( x , μ , λ ) ≤ m i n x m a x μ , λ , μ i ≥ 0 L ( x , μ , λ ) = p ∗ d^*=\underset{\mu,\lambda,\mu_i\geq0}{max}\underset{x}{min}L(x,\mu,\lambda)\leq \underset{x}{min}\underset{\mu,\lambda,\mu_i\geq0}{max}L(x,\mu,\lambda)=p^* d∗=μ,λ,μi≥0maxxminL(x,μ,λ)≤xminμ,λ,μi≥0maxL(x,μ,λ)=p∗
证明:对任意的 μ , λ , x \mu,\lambda,x μ,λ,x,有 θ D ( μ , λ ) = m i n x L ( x , μ , λ ) ≤ L ( x , μ , λ ) ≤ m a x μ , λ , μ i ≥ 0 L ( x , μ , λ ) = θ P ( x ) \theta_D(\mu,\lambda)=\underset{x}{min}L(x,\mu,\lambda)\leq L(x,\mu,\lambda)\leq \underset{\mu,\lambda,\mu_i\geq0}{max}L(x,\mu,\lambda)=\theta_P(x) θD(μ,λ)=xminL(x,μ,λ)≤L(x,μ,λ)≤μ,λ,μi≥0maxL(x,μ,λ)=θP(x)
由于原始问题和对偶问题均有最优值,所以 d ∗ = m a x μ , λ , μ i ≥ 0 θ D ( μ , λ ) ≤ m i n x θ P ( x ) = p ∗ d^*=\underset{\mu,\lambda,\mu_i\geq0}{max}\theta_D(\mu,\lambda)\leq \underset{x}{min}\theta_P(x)=p^* d∗=μ,λ,μi≥0maxθD(μ,λ)≤xminθP(x)=p∗
推论1(强对偶性: d ∗ = p ∗ d^*=p^* d∗=p∗)
设 x ∗ x^* x∗和 μ ∗ , λ ∗ \mu^*,\lambda^* μ∗,λ∗分别是原始问题和对偶问题的可行解,并且 d ∗ = p ∗ d^*=p^* d∗=p∗,则 x ∗ x^* x∗和 μ ∗ , λ ∗ \mu^*,\lambda^* μ∗,λ∗分别是原始问题和对偶问题的最优解
在某些条件下,原始问题和对偶问题的最优值相等,即 d ∗ = p ∗ d^*=p^* d∗=p∗,此时可以用解对偶问题替代解原始问题
定理2
假设 f ( x ) , g j ( x ) f(x),g_j(x) f(x),gj(x)是凸函数, h k ( x ) h_k(x) hk(x)是仿射函数(由一阶多项式构成的函数, h k ( x ) = A x + b h_k(x)=Ax+b hk(x)=Ax+b,A是矩阵,x、b是向量),并且假设不等式约束 g j ( x ) g_j(x) gj(x)是严格可行的,即存在x,对所有 j j j有 g j ( x ) < 0 g_j(x)<0 gj(x)<0,则存在 x ∗ , μ ∗ , λ ∗ x^*,\mu^*,\lambda^* x∗,μ∗,λ∗使 x ∗ x^* x∗是原始问题的解, μ ∗ , λ ∗ \mu^*,\lambda^* μ∗,λ∗是对偶问题的解,并且 d ∗ = p ∗ = L ( x ∗ , μ ∗ , λ ∗ ) d^*=p^*=L(x^*,\mu^*,\lambda^*) d∗=p∗=L(x∗,μ∗,λ∗)
定理3
假设 f ( x ) , g j ( x ) f(x),g_j(x) f(x),gj(x)是凸函数, h k ( x ) h_k(x) hk(x)是仿射函数,并且假设不等式约束 g j ( x ) g_j(x) gj(x)是严格可行的,则 x ∗ x^* x∗和 μ ∗ , λ ∗ \mu^*,\lambda^* μ∗,λ∗分别是原始问题和对偶问题的解的充要条件是 x ∗ , μ ∗ , λ ∗ x^*,\mu^*,\lambda^* x∗,μ∗,λ∗满足KKT条件
- 推论1、定理2、定理3的证明
2.4 对偶上升法
换个角度理解拉格朗日对偶函数
对优化问题 min f 0 ( x ) s.t. f i ( x ) ≤ 0 ( i = 1 , 2 , … , m ) h i ( x ) = 0 ( i = 1 , 2 , … , p ) \begin{array}{l}{\min f_0(x)} \\ {\text {s.t.} f_{i}(x) \leq 0(i=1,2, \ldots, m)} \\ {\;\;\;\;\;h_{i}(x)=0(i=1,2, \ldots, p)}\end{array} minf0(x)s.t.fi(x)≤0(i=1,2,…,m)hi(x)=0(i=1,2,…,p)
拉格朗日函数为 L ( x , λ , ν ) = f 0 ( x ) + ∑ i = 1 m λ i f i ( x ) + ∑ i = 1 p ν i h i ( x ) L(x, \lambda, \nu)=f_{0}(x)+\sum_{i=1}^{m} \lambda_{i} f_{i}(x)+\sum_{i=1}^{p} \nu_{i} h_{i}(x) L(x,λ,ν)=f0(x)+i=1∑mλifi(x)+i=1∑pνihi(x)
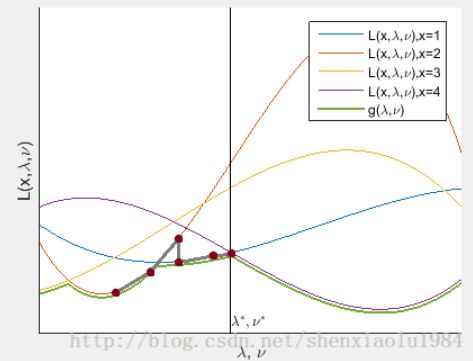
拉格朗日对偶函数为 g ( λ , ν ) = inf x ∈ D L ( x , λ , ν ) g(\lambda, \nu)=\inf _{x \in D} L(x, \lambda, \nu) g(λ,ν)=x∈DinfL(x,λ,ν)
可以将其看作是x取不同值时一簇曲线的下界(绿线)
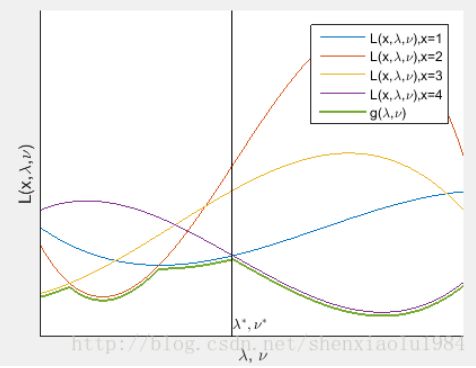
当 λ ≥ 0 \lambda\geq 0 λ≥0时,对于最优化问题的解 x ˉ \bar x xˉ,两个约束条件都非正: λ i f i ( x ˉ ) < = 0 , ν i h i ( x ˉ ) = 0 \lambda_{i} f_{i}(\bar{x})<=0, \nu_{i} h_{i}(\bar{x})=0 λifi(xˉ)<=0,νihi(xˉ)=0
于是,该解对应的曲线不超过原始问题最优解: L ( x ˉ , λ , ν ) ≤ f 0 ( x ˉ ) L(\bar{x}, \lambda, \nu) \leq f_{0}(\bar{x}) L(xˉ,λ,ν)≤f0(xˉ)
进一步,所有曲线的下界不超过原问题最优解: g ( λ , ν ) ≤ f 0 ( x ˉ ) g(\lambda, \nu) \leq f_{0}(\bar{x}) g(λ,ν)≤f0(xˉ)
换言之,拉格朗日对偶函数是最优化值的下界。又上图绿线上的最高点,是对最优值下界的最好估计,这个问题即为原始问题的拉格朗日对偶问题。如果强对偶条件成立,对偶问题存在最优解 λ ˉ , ν ˉ \bar \lambda,\bar \nu λˉ,νˉ,则原始问题 f 0 ( x ) f_0(x) f0(x)的最优解也是 L ( x , λ ˉ , ν ˉ ) L(x,\bar \lambda,\bar \nu) L(x,λˉ,νˉ)的最优解。 L ( x , λ ˉ , ν ˉ ) L(x,\bar \lambda,\bar \nu) L(x,λˉ,νˉ)是x的函数,相当于在图中 [ λ , ν ] = [ λ ˉ , ν ˉ ] [\lambda,\nu]=[\bar \lambda,\bar \nu] [λ,ν]=[λˉ,νˉ]对应的竖线上,查找值最小曲线对应的x。求解步骤归纳如下:
- 求解 max g ( λ , μ ) \max g(\lambda,\mu) maxg(λ,μ)得到 λ ˉ , ν ˉ \bar \lambda,\bar \nu λˉ,νˉ
- 求解 min L ( x , λ ˉ , ν ˉ ) \min L(x,\bar \lambda,\bar \nu) minL(x,λˉ,νˉ)得到 x ˉ \bar x xˉ
对偶上升法
设第k次迭代得到原始问题解为 x k x^k xk,对偶问题的解为 λ k , ν k \lambda^k,\nu^k λk,νk
- 假设 λ k , ν k \lambda^k,\nu^k λk,νk已为对偶问题的最优解,最小化 L ( x , λ k , ν k ) L(x,\lambda^k,\nu^k) L(x,λk,νk)得到原问题最优解 x k + 1 x^{k+1} xk+1 x k + 1 = arg min x L ( x , λ k , ν k ) x^{k+1}=\arg \min _{x} L\left(x, \lambda^{k}, \nu^{k}\right) xk+1=argxminL(x,λk,νk)
- 在该位置使用梯度上升法更新对偶问题的解: λ k + 1 = λ k + α ⋅ ∂ L ( x , λ , ν ) ∂ λ ∣ x = x k + 1 , λ = λ k , ν = ν k ν k + 1 = λ k + α ⋅ ∂ L ( x , λ , ν ) ∂ ν ∣ x = x k + 1 , λ = λ k , ν = ν k \begin{aligned} \lambda^{k+1} &=\lambda^{k}+\left.\alpha \cdot \frac{\partial L(x, \lambda, \nu)}{\partial \lambda}\right|_{x=x^{k+1}, \lambda=\lambda^{k}, \nu=\nu^{k}} \\ \nu^{k+1} &=\lambda^{k}+\left.\alpha \cdot \frac{\partial L(x, \lambda, \nu)}{\partial \nu}\right|_{x=x^{k+1}, \lambda=\lambda^{k}, \nu=\nu^{k}} \end{aligned} λk+1νk+1=λk+α⋅∂λ∂L(x,λ,ν)∣∣∣∣x=xk+1,λ=λk,ν=νk=λk+α⋅∂ν∂L(x,λ,ν)∣∣∣∣x=xk+1,λ=λk,ν=νk
2.5 对偶分解法
假设目标函数是可分解的: f ( x ) = ∑ i = 0 n f i ( x i ) s.t. A x = b , ∀ x = ( x 0 , x 1 , ⋯ , x n ) T \begin{array}{l}{f(x)=\sum_{i=0}^{n} f_{i}\left(x_{i}\right)} \\ {\text { s.t. } \quad A x=b, \forall x=\left(x_{0}, x_{1}, \cdots, x_{n}\right)^{T}}\end{array} f(x)=∑i=0nfi(xi) s.t. Ax=b,∀x=(x0,x1,⋯,xn)T
则拉格朗日函数是可分解的: L ( x , λ ) = ∑ i = 0 n L ( x i , λ ) = ∑ i = 0 n f i ( x i ) + λ A i x − λ b i \begin{aligned} L(x, \lambda) &=\sum_{i=0}^{n} L\left(x_{i}, \lambda\right) \\ &=\sum_{i=0}^{n} f_{i}\left(x_{i}\right)+\lambda A_{i} x-\lambda b_{i} \end{aligned} L(x,λ)=i=0∑nL(xi,λ)=i=0∑nfi(xi)+λAix−λbi
所以对偶上升法中的第一步可以修改为 x i k + 1 = arg min x i L i ( x i , λ k ) x_{i}^{k+1}=\arg \min _{x_{i}} L_{i}\left(x_{i}, \lambda^{k}\right) xik+1=argximinLi(xi,λk)即可并行计算 x k + 1 x^{k+1} xk+1的每个元素,从而快速得到 x k + 1 x^{k+1} xk+1
3 内外点罚函数法
罚函数的基本思想是构造辅助函数,把原来的约束问题转化为求极小化辅助函数的无约束问题,如何构造辅助函数是求解问题的首要问题。
3.1 外点罚函数法
构造辅助函数 F μ : R n → R ( μ > 0 ) F_\mu:\mathbb{R}^n\rightarrow\mathbb{R}(\mu>0) Fμ:Rn→R(μ>0),构造函数在可行域内部与原问题的取值相同,在可行域外部取值远远大于目标函数的取值
-
对于等式约束问题: m i n f ( x ) s . t . h k ( x ) = 0 ( k = 1 , 2 , … , m ) \begin{aligned}&minf(x) \\ &s.t.\;h_k(x)=0(k=1,2,\dots ,m)\end{aligned} minf(x)s.t.hk(x)=0(k=1,2,…,m)可定义辅助函数: F ( x , μ ) = f ( x ) + μ ∑ k = 1 m h k 2 ( x ) F(x,\mu)=f(x)+\mu\sum_{k=1}^mh_k^2(x) F(x,μ)=f(x)+μk=1∑mhk2(x)
-
对于不等式约束问题: m i n f ( x ) s . t . g j ( x ) ≤ 0 ( j = 1 , 2 , … , l ) \begin{aligned}&minf(x) \\ &s.t.\;g_j(x)\leq0(j=1,2,\dots ,l)\end{aligned} minf(x)s.t.gj(x)≤0(j=1,2,…,l)可定义辅助函数: F ( x , μ ) = f ( x ) + μ ∑ j = 1 l ( m a x { 0 , g j ( x ) } ) 2 F(x,\mu)=f(x)+\mu\sum_{j=1}^l(max\{0,g_j(x)\})^2 F(x,μ)=f(x)+μj=1∑l(max{0,gj(x)})2
-
对于一般问题,可定义辅助函数: F ( x , μ ) = f ( x ) + μ P ( x ) F(x,\mu)=f(x)+\mu P(x) F(x,μ)=f(x)+μP(x)其中 P ( x ) = ∑ j = 1 l ϕ ( g j ( x ) ) + ∑ k = 1 m ψ ( h k ( x ) ) P(x)=\sum_{j=1}^l\phi(g_j(x))+\sum_{k=1}^m\psi(h_k(x)) P(x)=j=1∑lϕ(gj(x))+k=1∑mψ(hk(x)) ϕ ( z ) { = 0 , z ≤ 0 > 0 , z > 0 , ψ ( z ) { = 0 , z = 0 > 0 , z ≠ 0 \phi(z)\left\{\begin{array}{l}=0,z\leq0\\>0,z>0\end{array}\right.,\psi(z)\left\{\begin{array}{l}=0,z=0\\>0,z\neq0\end{array}\right. ϕ(z){=0,z≤0>0,z>0,ψ(z){=0,z=0>0,z=0典型取法有 ϕ = ( m a x { 0 , g j ( x ) } ) α , ψ = ∣ h k ( x ) ∣ β , α ≥ 1 , β ≥ 1 \phi=(max\{0,g_j(x)\})^\alpha,\psi=\vert h_k(x)\vert^\beta,\alpha\geq1,\beta\geq1 ϕ=(max{0,gj(x)})α,ψ=∣hk(x)∣β,α≥1,β≥1
通过这些辅助函数,可以把约束问题转换为无约束问题 m i n F ( x , μ ) minF(x,\mu) minF(x,μ),其中 μ \mu μ是很大的数,通常取一个趋向于无穷大的严格递增正数列 { μ k } \{\mu_k\} {μk}
具体步骤:
- 给定初始点 x ( 0 ) x^{(0)} x(0),初始罚因子 μ 1 \mu_1 μ1,放大系数 c > 0 c>0 c>0,允许误差 ϵ > 0 \epsilon>0 ϵ>0,设 k = 1 k=1 k=1
- 以 x ( k − 1 ) x^{(k-1)} x(k−1)为初始点,求解无约束问题 m i n F ( x , μ ) = f ( x ) + μ k P ( x ) minF(x,\mu)=f(x)+\mu_kP(x) minF(x,μ)=f(x)+μkP(x),得极小点 x ( k ) x^{(k)} x(k)
- 若 μ k P ( x ( k ) ) < ϵ \mu_kP(x^{(k)})<\epsilon μkP(x(k))<ϵ,停止,得极小点 x ( k ) x^{(k)} x(k);否则,令 μ k + 1 = c μ k , k = k + 1 \mu_{k+1}=c\mu_k,k=k+1 μk+1=cμk,k=k+1,转步骤二
3.2 内点罚函数法
从可行域内部逼近问题的解,构造辅助函数,使得该函数在严格可行域外无穷大,当自变量趋于可行域边界时,函数值趋于无穷大。适用于不等式约束问题: m i n f ( x ) s . t . g j ( x ) ≤ 0 ( j = 1 , 2 , … , l ) \begin{aligned}&minf(x) \\ &s.t.\;g_j(x)\leq0(j=1,2,\dots ,l)\end{aligned} minf(x)s.t.gj(x)≤0(j=1,2,…,l)
可行域为 S = { x ∣ g j ( x ) ≤ 0 , j = 1 , 2 , … , l } S=\{x\vert g_j(x)\leq0,j=1,2,\dots ,l\} S={x∣gj(x)≤0,j=1,2,…,l}
定义障碍函数: F ( x , μ ) = f ( x ) + μ B ( x ) F(x,\mu)=f(x)+\mu B(x) F(x,μ)=f(x)+μB(x)当自变量趋于可行域边界时, B ( x ) → + ∞ B(x)\rightarrow +\infty B(x)→+∞,当 μ → 0 \mu\rightarrow0 μ→0时, m i n F μ minF_\mu minFμ的解趋于原始问题的解
常用辅助函数 B ( x ) = ∑ j = 1 l − 1 g j ( x ) B(x)=\sum_{j=1}^l-\frac1{g_j(x)} B(x)=j=1∑l−gj(x)1 B ( x ) = − ∑ j = 1 l ln ( − g j ( x ) ) B(x)=-\sum_{j=1}^l\ln (-g_j(x)) B(x)=−j=1∑lln(−gj(x))
具体步骤:
- 给定初始点 x ( 0 ) x^{(0)} x(0),初始罚因子 μ 1 \mu_1 μ1,缩小系数 β ∈ ( 0 , 1 ) \beta\in (0,1) β∈(0,1),允许误差 ϵ > 0 \epsilon>0 ϵ>0,设 k = 1 k=1 k=1
- 以 x ( k − 1 ) x^{(k-1)} x(k−1)为初始点,求解无约束问题 m i n F ( x , μ ) = f ( x ) + μ k B ( x ) minF(x,\mu)=f(x)+\mu_kB(x) minF(x,μ)=f(x)+μkB(x),得极小点 x ( k ) x^{(k)} x(k)
- 若 μ k B ( x ( k ) ) < ϵ \mu_kB(x^{(k)})<\epsilon μkB(x(k))<ϵ,停止,得极小点 x ( k ) x^{(k)} x(k);否则,令 μ k + 1 = β μ k , k = k + 1 \mu_{k+1}=\beta\mu_k,k=k+1 μk+1=βμk,k=k+1,转步骤二
4 参考资料
- 浅谈最优化问题的KKT条件
- 《统计学习方法》(李航)附录C
- 拉格朗日函数、对偶上升法、对偶分解法
- 【优化】对偶上升法(Dual Ascent)超简说明
- 罚函数法求解约束问题最优解