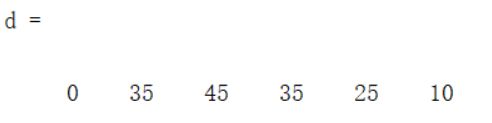美国数学建模大赛（matlab自学）之最短路问题

图与网络模型与方法

图与网络数据结构

邻接矩阵表示法

当G为赋权图时：

当G为无权图时：

稀疏矩阵表示法

指矩阵当中零元素很多，非零元素很少的矩阵
稀疏矩阵只是一种存储格式，Matlab中，普通矩阵使用sparse命令变成稀疏矩阵，稀疏矩阵使用full命令变成普通矩阵

最短路问题

Dijksyra算法

例题：

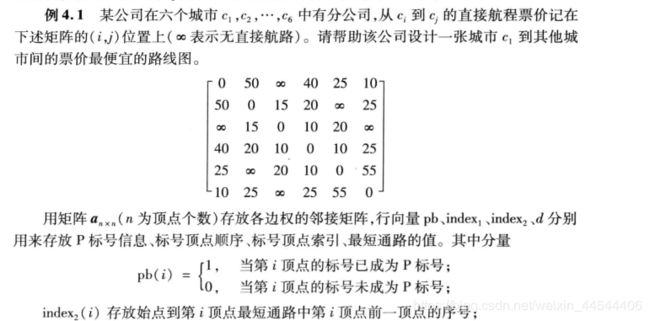
a=zeros(6);
a(1,2)=50;a(1,4)=40;a(1,5)=25;a(1,6)=10;               
a(2,3)=15;a(2,4)=20;a(2,6)=25;
a(3,4)=10;a(3,5)=20;
a(4,5)=10;a(4,6)=25;
a(5,6)=55;
a=a+a'                                                  
a(find(a==0))=inf              
pb(1:length(a))=0;pb(1)=1;  
index1=1; %存放存入S集合的顺序
index2=ones(1,length(a)); %全1矩阵，存放始点到第i点最短通路中第i顶点前一顶点的序号
d(1:length(a))=inf;d(1)=0;  %存放由始点到第i点最短通路的值
temp=1;  %最新P标号的顶点
while sum(pb)

结果：

模板

function [mydistance ,mypath] = mydijkstra(a,sb,db); 
%输入:a一邻接矩阵;a(i,j)-i到j之间的距离,可以是有向的
%sb起点的标号, db-终点的标号
%输出:mydistance-最短路的距离，mypath-最短路的路径
n=size(a,1); %获取矩阵a的行数
visited(1:n) = 0;%访问标记数组初始化为0
distance(1:n) = inf;%距离初始化为最大值
 distance(sb) = 0;
visited(sb) =1; u=sb; % u为最新的P标号顶点
parent(1:n) = 0;%前驱顶点的初始化
for i = 1:n-1
  id= find(visited= =0); %查找未标号的顶点
  for v=id:
       if a(u, v) + distance(u) < distance(v)
         distance(v) = distance(u) + a(u, v);号修改标号值
         parent(v) = u;%v的上一个顶点是u
       end
end
temp = distance;
temp(visited= =1) =inf;%已标号点的距离换成无穷
[t,u] = min(temp);%找标号值最小的顶点
visited(u) = 1;%标记已经标号的顶点
end
mypath = [];
if parent(ab)~= 0%如果存在路~=不等于
t = db; 
mypath = [db];
while t~= sb
P= parent(t);
mypath = [ P mypath]; 
t=p;
end
end
mydistance = distance( ab);

Floyd算法

求解每对顶点的最短路径

例题的代码：

clear;clc;

n=6; a= zeros(n) ;

a(1,2) =50;a(1,4) =40;a(1,5) =25;a(1,6) =10;

a(2,3) =15;a(2,4) =20;a(2,6) =25; 
a(3,4) =10;a(3,5) =20;
a(4,5) =10;a(4,6) =25; 
a(5,6) =55;a=a+a';
a(a==0) =inf;%把所有零元素替换成无穷
a([1:n+1:n^2])=0; %对角线元素替换成零,Matlab中数据是逐列存储的
path = zeros(n) ;
for k=1:n
  for i=1:n
     for j =1:n
       if a(i,j) >a(i,k) +a(k,j)
       a(i,j) =a(i,k) +a(k,j);
       path(i,j) =k;
      end
     end
   end
end
a, path

模板：

 function [dist ,mypath] = myfloyd(a,sb, db);
%输入:a邻接矩阵;元素a(i,j)——顶点i到j之间的直达距离,可以是有向的
%sb起点的标号;db终点的标号
%输出:dist-最短路的距离;
%mypath一最短路的路径 
n=size(a,1); path = zeros(n);
for k=1:n
   for i=1:n
     for j=1:n
        if a(i,j) >a(i,k) +a(k,j)
          a(i,j) =a(i,k) +a(k,j);
          path(i,j) =k;
        end
      end
    end
end
dist =a(sb,ab);
parent =path(sb,:);%从起点sb到终点ab的最短路上各顶点的前驱顶点
parent(parent==0) =sb;%path中的分量为0,表示该顶点的前驱是起点
mypath=ab; t = ab;
while t~=sb
	P = parent(t); 
	mypath=[p,mypath];
	t =P;
end