数据结构随笔——图的基本概念及最小生成树
一、图的基本概念及术语
图( Graph )是由顶点的有穷非空集合和顶点之间边的集合组成,通常表示为: G(V,E),其中,G表示一个图,V是图G中顶点的集合,E是图G中边的集合。
无向边:若顶点v到Vj之间的边没有方向,则称这条边为无向边(Edge), 用无序偶对(Vi,Vj) 来表示。
如果图中任意两个顶点之间的边都是无向边,则称该图为无向图。
有向边 :若从顶点w到v的边有方向,则称这条边为有向边,也称为弧。用有序偶
在无向图中,如果任意两个顶点之间都存在边,则称该图为无向完全图。含有n个顶点的无向完全图有n(n-1)/2条边。在有向图中,如果任意两个顶点之间都存在方向互为相反的两条弧,则称该图为有向完全图。含有n个顶点的有向完全图有n (n-1)条边。
有些图的边或弧具有与它相关的数字,这种与图的边或弧相关的数叫做权(Weight)。这些权可以表示从一个顶点到另一个顶点的距离或耗费。这种带权的图通常称为网(Network)。
对于无向图G= (V,{E}), 如果边(v,v’) ∈E,则称顶点v和v’互为邻接点(Adjacent),即v和v’相邻接。边(v,v’) 依附(incident) 于顶点v和v’,或者说(v,v’)与顶点v和v’相关联。顶点v的度(Degree) 是和v相关联的边的数目。
对于有向图G= (V,{E}), 如果弧顶点v的度为TD (v) =ID (v) +OD (v)
在无向图G中,如果从顶点v到顶点v’有路径,则称v和v’是连通的。如果对于图中任意两个顶点vi、 vj∈E, vi和vj都是连通的,则称G是连通图(Connected Graph)。
在有向图G中,如果对于每一对 vi、vj∈V、vi≠vj,从vi到vj和从vj到vi 都存在路径,则称G是强连通图。有向图中的极大强连通子图称做有向图的强连通分量。
二、图的存储结构
1.邻接矩阵
#define MAXVEX 100 //最大顶点数
#define INF 65535 //代表无穷大
typedef struct
{
int vexs[MAXVEX];//顶点表
int arc[MAXVEX][MAXVEX];
int num_vertexes, num_edges;//顶点数,边数
}mgraph;
void create_mgraph(mgraph* G)
{
cin >> G->num_vertexes >> G->num_edges;
//输顶点数,边数
for (int i = 0; i < G->num_vertexes; i++)
cin >> G->vexs[i];
//邻接矩阵初始化:
for (int i = 0; i < MAXVEX; i++)
{
for (int j = 0; j < MAXVEX; j++)
G->arc[i][j] = INF;
}
int vi, vj, w;
for (int i = 0; i < G->num_vertexes; i++)
{
cin >> vi >> vj >> w;
G->arc[vi][vj] = G->arc[vj][vi] = w;
}
}
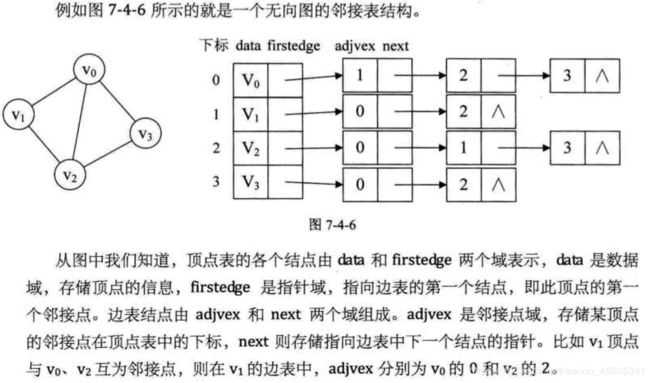
2.邻接表
#define MAXVEX 100
typedef char vertex_type; //顶点类型
typedef int edge_type; //权值类型
typedef struct edge_node
{
int adjvex; //邻接点域,存储该点下标
edge_type weight; //权值
struct edge_node* next; //指向下一个邻接点
}edgenode;
typedef struct vertex_node //顶点表节点
{
edge_type data;
edge_node* first_edge; //边表头指针
}vertexnode,AdjList[MAXVEX];
typedef struct
{
AdjList adjlist;
int num_vertexes, num_edges;//顶点数,边数
}graphadjlist;
void create_graphadjlist(graphadjlist* G)
{
edge_node* e;
cin >> G->num_vertexes >> G->num_edges;
for (int i = 0; i < G->num_vertexes; i++)
{
cin >> G->adjlist[i].data;
G->adjlist[i].first_edge = NULL;//将边表置为空表
}
//建立边表,对于无向图要插入两次
for (int i = 0; i < G->num_edges; i++)
{
int vi, vj;
cin >> vi >> vj;
e = (edge_node *)malloc(sizeof(edge_node));
e->adjvex = vj;
e->next = G->adjlist[vi].first_edge;
G->adjlist[vi].first_edge = e;
e = (edge_node*)malloc(sizeof(edge_node));
e->adjvex = vi;
e->next = G->adjlist[vj].first_edge;
G->adjlist[vj].first_edge = e;
}
}
无向图中顶点vi的度为第i个单链表中的结点数
有向图中顶点vi的出度为第i个单链表中的结点个数,顶点vi的入度为整个单链表中邻接点域值是i的结点个数(以vi为弧头)
邻接矩阵多用于稠密图的存储(e接近n(n-1)/2)。而邻接表多用于稀疏图的存储( e<
三、图的遍历
深度优先遍历(Depth, First Search),也有称为深度优先搜索,简称为DFS。深度优先遍历其实就是一个递归的过程,就像是一-棵树的前序遍历。
它从图中某个顶点v出发,访问此顶点,然后从v的未被访问的邻接点出发深度优先遍历图,直至图中所有和v有路径相通的顶点都被访问到。
#define MAXVEX 100 //最大顶点数
#define INF 65535 //代表无穷大
typedef struct
{
int vexs[MAXVEX];//顶点表
int arc[MAXVEX][MAXVEX];
int num_vertexes, num_edges;//顶点数,边数
}mgraph;
bool visited[MAXVEX];
//邻接矩阵的DFS
void dfs(mgraph G, int i)
{
visited[i] = true;
cout << i << endl;//打印顶点
for (int j = 0; j < G.num_vertexes; j++)
{
if (G.arc[i][j] == 1 && !visited[j])
dfs(G, j);
}
}
void dfs_traverse(mgraph G)
{
for (int i = 0; i < G.num_vertexes; i++)
visited[i] = false;
for (int i = 0; i < G.num_vertexes; i++)
if (!visited[i])
dfs(G, i);//每个顶点搜索,如果是连通图只会执行一次
}
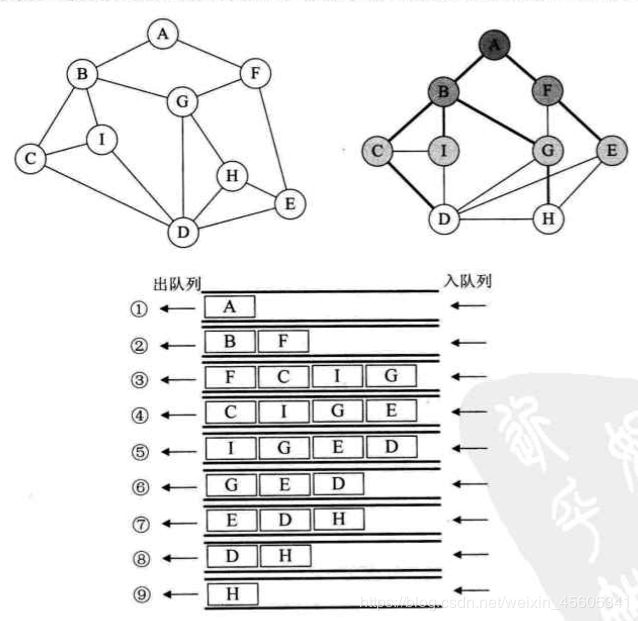
广度优先遍历(Breadth First Search),又称为广度优先搜索,简称BFS。如果说图的深度优先遍历类似树的前序遍历,那么图的广度优先遍历就类似于树的层序遍历了。
void bfs(mgraph G)
{
queue < int > q;
for (int i = 0; i < G.num_vertexes; i++)
visited[i] = false;
for (int i = 0; i < G.num_vertexes; i++)
{
if (!visited[i])
{
visited[i] = true;
cout << G.arc[i] << endl;//打印顶点
q.push(G.vexs[i]);
while (!q.empty())
{
q.pop();//出队列
for (int j = 0; j < G.num_vertexes; j++)
{
if (G.arc[i][j] == 1 && !visited[j])
//有边且该顶点未被访问
{
visited[j] = true;
cout << G.vexs[j] << endl;
q.push(G.vexs[j]);
}
}
}
}
}
}
四、最小生成树
推荐教程,王道考研-数据结构-最小生成树
1.Prim算法
简单来说就是:将顶点分成两个部分,U(选中的部分),V(未选中的部分)。每次从两个部分中找出权值最小的边相连的顶点划入U中。重复上述步骤,直到顶点全部划入U中
复杂度在O(n^2)
我们需要建立两个数组,lowcost,保存顶点权值,和adjvex,保存顶点。首先要初始化,令一个点为第一个点,lowcost初始化为与其相连的点的边权值,adjvex值初始化为改点。而后循环:在lowcost中找到最小且不能为0(因为为0代表改点已经加入生成树),保存该权值及下标,将这个位置的lowcost值置为0,这就是生成树的一个边。更新lowcost数组,如果遇到与刚刚添加的点有边的且权值小于lowcost该位置的权值,则赋值给lowcost,同时把该位置的adjvex赋值为下标。结束循环,adjvex的数组下标与值的关系就是最小生成树。
#include2.Kruskal算法
简单描述:转化为边集数组,从小到大排序,然后循环每一条边,依次加入(如果形成一个环则不可以加入)。
复杂度:O(nlogn) n为边数
#define MAXVEX 100
#define MAXEDGE 200
typedef struct node
{
int weight; //长度
int begin; //边的起点
int end; //边的终点
}Edge;
typedef struct
{
int vexs[MAXVEX];//顶点表
int arc[MAXVEX][MAXVEX];
int num_vertexes, num_edges;//顶点数,边数
}mgraph;
int find(int* parent, int f)
{
while (parent[f]>0)
f = parent[f];
return f;
}
void kruskal(mgraph g)
{
int n, m;
Edge edges[MAXEDGE];//定义边集数组
int parent[MAXEDGE];//判断是否形成回路
//!!!将邻接矩阵变为边集数组再按照权值从小到达排序(此处省略)
for (int i = 0; i <= MAXEDGE; i++)
parent[i] = 0;
for (int i = 0; i < g.num_edges; i++)//循环每一条边
{
n = find(parent, edges[i].begin);
m = find(parent, edges[i].end);
if (n != m)
{
parent[n] = m;
//将结尾点放置在下标为开始点的位置上,表示已经加入生成树
cout << edges[i].begin << edges[i].end << edges[i].weight << endl;
}
}
}