- 视频学习心得及问题总结
- 1.1 深度学习的数学基础
- 1.2 卷积神经网络
- 1.3 ResNet
- 代码练习
- 2.1 MNIST 数据集分类
- 2.2 CIFAR10 数据集分类
- 2.3 使用VGG16 对 CIFAR10分类
- 2.4 使用VGG模型迁移学习进行猫狗大战
- 展望学习
- 3.1 googLeNet Inception V1
- 3.2 googLeNet Inception V2
- 3.3 googLeNet Inception V3
- 3.4 googLeNet Inception V4
- 3.5 mobileNet
- 3.6 HybridSN
视频学习心得及问题总结
1.1 深度学习的数学基础
-
深层网络的局部极小值问题主要是由于隐层复合导致的。凸的激活函数在多层复合的情况下一般不是凸的。在深度学习训练过程中经常会陷入鞍点这类的驻点,这一般是由于参数维度过高导致的。
-
机器学习需要的数学一般有线性代数,概率论和最优化问题
-
线性变换
\[T(x)=Ax \]如果矩阵A存在某个特征值λ,存在特定的向量x不为0,使得
\[Ax=λx \]那么矩阵A对该特定的向量x的效果仅仅是进行一个与x同方向(或反方向)的伸缩。
若存在任意向量x不为矩阵A的特征向量,做变换
\[T(x)=A^nx \]那么在n足够大的情况下,该变换结果会无限趋近于矩阵A的最大特征值对应的特征向量的方向(正反两个方向)
-
矩阵对向量的作用是进行旋转和伸缩
-
矩阵的秩的含义是表示这个矩阵需要的最小的基的数量,秩越小,需要的基越小
-
若矩阵表达的为结构化的信息,各行存在一定相关性,那么秩一般比较低
-
对矩阵A做奇异值分解
\[A_{n×d}=U_{n×r}\Sigma_{r×r}V_{r×d}^T \]可以对矩阵A进行降维,A的前r个较大的特征之可以包含A的足够信息。该模式可以用于图像去噪
-
梯度下降是神经网络的重要数学基础
-
机器学习三要素包括模型(问题模型)、策略(目标函数)和算法(求解参数)
-
无免费午餐定理
当考虑在所有问题上的平均性能时,任意两个模型都是相同的
-
奥卡姆剃刀原理
形式简单的答案往往是正确的。过于接近训练集会导致过拟合
-
过拟合的解决方案有:增大训练集,降低模型复杂度
1.2 卷积神经网络
-
深度学习三部曲:搭建神经网络结构,找到一个合适的损失函数,找到一个合适的优化函数,更新参数
-
softmax函数用以归一化概率
-
传统神经网络之所以不适合直接用于计算机视觉是因为这会导致参数量过多。参数过多将会导致过拟合
-
卷积神经网络中卷积核的参数是共享的,这会大大降低需要计算的参数量
-
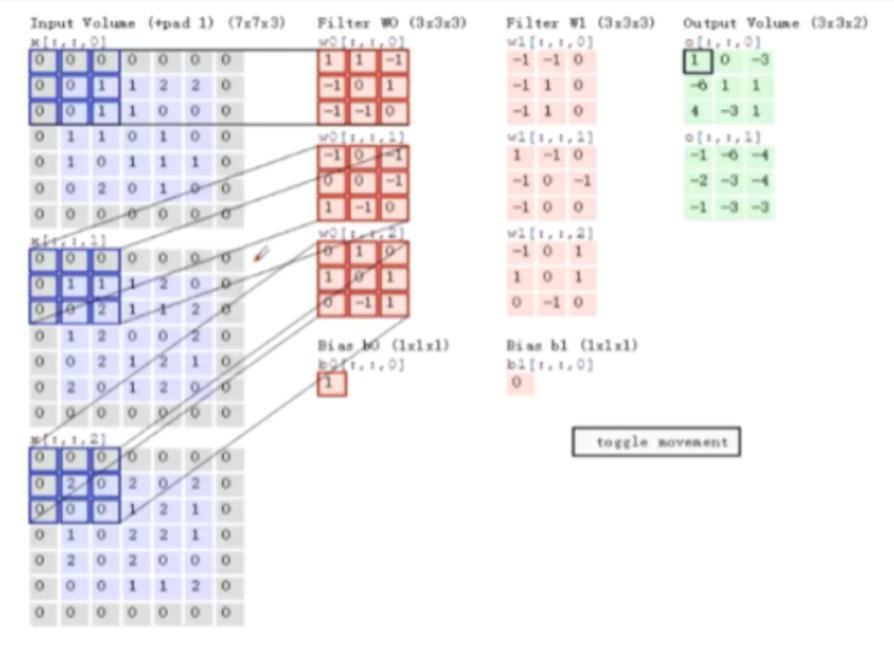
卷积的计算方式
-
卷积后输出特征图的大小为:
\[dim_{map}=(N-F)/stride+1 \](不加padding时) 其中N为输入维度,F为卷积核维度,stride为步长,带有padding时的计算公式为
\[dim_{map}=(N+2padding-F)/stride+1 \] -
池化可以保留主要特征的同时减少参数和计算量,防止过拟合。池化往往处于卷积层和卷积层和全连接层和全连接层之间
-
池化操作为
-
池化分为最大值池化和平均池化。分类任务中使用最大值池化可以取得相对较好的效果
-
在神经网络最后往往会增加一个全连接层
-
ReLU函数的优点
- 很好的改善了梯度消失问题
- 计算速度很快,仅需要判断输入是否大于0
- 收敛速度很快
-
dropout(随机失活)就是训练的时候随机部分神经元(这可以减少参数量,防止过拟合),测试时整合所有神经元
-
神经网络中参数是由卷积层贡献的,激活函数和池化操作不存在参数
-
AlexNet的结构为
(卷积->ReLU->池化)->(卷积->ReLU->池化)->(卷积->ReLU)->(卷积->ReLU)->
(卷积->ReLU->池化)->(全连接->ReLU->DropOut)->(全连接->ReLU->DropOut)->
(全连接->SoftMax)
-
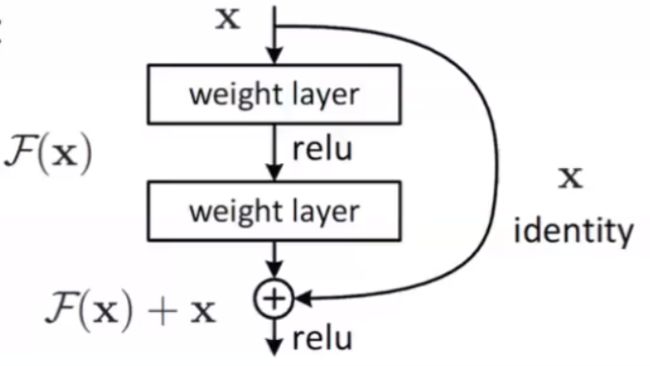
Res残差网络的特性
- 解决梯度消失
- 由于输出总会加入有全部的输入,导致输出大于输入,减缓梯度消失
- 灵活
- 由于输出含有输入的部分,如果本层的输出与输入相同,可以认为本层不起作用,所以网络可以根据自己的需要调整网络的深度
- 解决梯度消失
1.3 ResNet
-
代码练习
2.1 MNIST数据分类
-
本分类任务是进行手写数字的识别,类别共有10类(0~9)。分别用两种不同的模型
第一种是全连接网络,其结构为
self.network = nn.Sequential( nn.Linear(input_size, n_hidden), nn.ReLU(), nn.Linear(n_hidden, n_hidden), nn.ReLU(), nn.Linear(n_hidden, output_size), nn.LogSoftmax(dim=1) )三个线性模型之后接上一个softmax函数以归一概率。
\[→linear→8→ReLU→8→linear→8→ReLU→8→linear→ \],数字代表神经元个数
第二种是卷积神经网络模型,其结构为
x = self.conv1(x) x = F.relu(x) x = F.max_pool2d(x, kernel_size=2) x = self.conv2(x) x = F.relu(x) x = F.max_pool2d(x, kernel_size=2) x = x.view(-1, self.n_feature*4*4) x = self.fc1(x) x = F.relu(x) x = self.fc2(x) x = F.log_softmax(x, dim=1) CNN( (conv1): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1)) (conv2): Conv2d(6, 6, kernel_size=(5, 5), stride=(1, 1)) (fc1): Linear(in_features=96, out_features=50, bias=True) (fc2): Linear(in_features=50, out_features=10, bias=True) )\[ 28×28×1→conv1(5×5)→24×24×6→ReLU→pooling(2×2)→12×12×6→\\ conv2(5×5)→8×8×6→ReLU→pooling(2×2)→4×4×6(96)→\\fc1→50→ReLU→fc2→10→softmax \]卷积层参数数量计算公式为:
\[ 卷积层参数数量=(核长×核宽×输入通道数+单个卷积核偏置项数量(1))×核数 \]线性层参数数量计算公式为:
\[ 线性层参数数量=输入参数数量×输出参数数量+偏置项数量(输出参数数量) \]\[ Q_{conv1}=(5×5×1+1)×6×1=156\\Q_{conv2}=(5×5×6+1)×6=906\\ Q_{linear1}=96×50+50=4850\\Q_{linear2}=50×10+10=510 \]conv1参数个数为(5×5×1+1)×6×1=156, conv2:(5×5×6+1)×6, linear1:96×50+50,linear2:50*10+10
我们查看一下给出的结构以做对比
与结果一致
-
有关a = a[:,p]
p = torch.randperm(10) print(p) a = torch.tensor([0,1,2,3,4,5,6,2,8,9]) print(a) a = a.view(-1,10) print(a) a = a[:,p] print(a)输出结果为:
tensor([8, 6, 3, 7, 5, 0, 2, 1, 4, 9]) tensor([0, 1, 2, 3, 4, 5, 6, 2, 8, 9]) tensor([[0, 1, 2, 3, 4, 5, 6, 2, 8, 9]]) tensor([[8, 6, 3, 2, 5, 0, 2, 1, 4, 9]])a[:,p]会按照p中的数值,将原来a中的第p[i]个数放在p[i]当前所属的a[j]的位置
-
图像识别问题中,卷积神经网络要优于全连接神经网络
-
由于卷积神经网络利用卷积进行计算,所以在打乱像素顺序后,准确率下降很快。
2.2 CIFAR10 数据集分类
-
本模型与上一个模型相比增加了一个线性层,具体代码结构与上一个基本一致
\[→conv1→ReLU→pooling→conv2→ReLU→pooling→\\fc1→ReLU→fc2→ReLU→f3→ \] -
在训练中有几个固定的操作需要实现
#根据当前模型的参数计算输出值 outputs = model(inputs) #梯度清零 optimizer.zero_grad() #计算损失 loss = criterion(outputs, labels) #反向传播 loss.backward() #更新参数 optimizer.step()
2.3 使用VGG16对CIFAR10分类
-
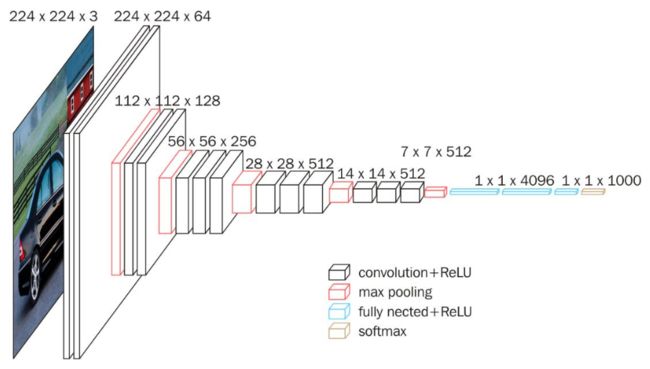
下图可以很好的说明VGG16的模型结构
16层网络的结节信息如下:
- 01:Convolution using 64 filters
- 02: Convolution using 64 filters + Max pooling
- 03: Convolution using 128 filters
- 04: Convolution using 128 filters + Max pooling
- 05: Convolution using 256 filters
- 06: Convolution using 256 filters
- 07: Convolution using 256 filters + Max pooling
- 08: Convolution using 512 filters
- 09: Convolution using 512 filters
- 10: Convolution using 512 filters + Max pooling
- 11: Convolution using 512 filters
- 12: Convolution using 512 filters
- 13: Convolution using 512 filters + Max pooling
- 14: Fully connected with 4096 nodes
- 15: Fully connected with 4096 nodes
- 16: Softmax
-
本模型训练时会报错如下
--------------------------------------------------------------------------- RuntimeError Traceback (most recent call last)in () 6 optimizer.zero_grad() 7 # 正向传播 + 反向传播 + 优化 ----> 8 outputs = net(inputs) 9 loss = criterion(outputs, labels) 10 loss.backward() 4 frames /usr/local/lib/python3.6/dist-packages/torch/nn/functional.py in linear(input, weight, bias) 1608 if input.dim() == 2 and bias is not None: 1609 # fused op is marginally faster -> 1610 ret = torch.addmm(bias, input, weight.t()) 1611 else: 1612 output = input.matmul(weight.t()) RuntimeError: size mismatch, m1: [128 x 512], m2: [2048 x 10] at /pytorch/aten/src/THC/generic/THCTensorMathBlas.cu:283 其中
m1: [128 x 512], m2: [2048 x 10]容易引起误解,乘号不是表达矩阵行列的分割,而是输入输出的分隔,现在前面一层输入128,输出512,后面一层输入2048,输出10,512与2048不匹配,导致问题出现。
仅需把最后一层的输入修改为512即可解决该问题。
若采用与猫狗大战相同的模型进行训练测试,损失函数使用交叉熵,batch size改为128,那么准确率如下:
并不比该模型优秀。具体原因还在探索之中。
2.4 使用VGG模型迁移学习进行猫狗大战
import torch import torch.nn as nn from torchvision import models,transforms,datasets device = torch.device("cuda" if torch.cuda.is_available() else "cpu") print('Using GPU: %s' % torch.cuda.is_available())#下载数据并解压 ! wget http://fenggao-image.stor.sinaapp.com/dogscats.zip ! unzip dogscats.zip#创建训练集文件夹,其中./表示content文件夹,注意该文件夹下需要有特定的格式,必须在train或者valid文件 #夹下存有分类,在本任务中为两个文件夹cat和dog,文件夹内放入的是各自类别的图片 train_set = datasets.ImageFolder('./dogscats/train', transforms.Compose([ transforms.CenterCrop(224), transforms.ToTensor(), transforms.Normalize(mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225]), ])) #创建测试集文件夹 test_set = datasets.ImageFolder('./dogscats/valid', transforms.Compose([ transforms.CenterCrop(224), transforms.ToTensor(), transforms.Normalize(mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225]), ]))#创建loader以分批操作数据,batch size会影响最终的性能,需要仔细分析调节测试 train_loader = torch.utils.data.DataLoader(train_set, batch_size=40, shuffle=True, num_workers=6) test_loader = torch.utils.data.DataLoader(test_set, batch_size=5, shuffle=True, num_workers=6)#选择VGG16模型 VGG_model_SGD = models.vgg16(pretrained=True) VGG_model_Adam = models.vgg16(pretrained=True) #由于下载的VGG模型已经预训练好,所以我们需要将前面的参数更新操作停止,仅需要更新最后一层的参数就可以达到很好的效果。这是迁移学习的特点。 for p in VGG_model_SGD.parameters(): p.requires_grad = False #还需要将下载下来的模型调整一下网络结果,以适用于本次的学习任务。将最后一层的输出改为2即可.通过查看该网络的结构,知道最后一层在classifier的第六层 VGG_model_SGD.classifier._modules['6'] = nn.Linear(4096, 2) #使用softmax函数来避免负值,把他添加在最后一层来激活,dim参数为0表示对列进行归一,为1表示对行进行归一 VGG_model_SGD.classifier._modules['7'] = nn.LogSoftmax(dim=1) #用同样的方法训练第二个模型以进行比较 for p in VGG_model_Adam.parameters(): p.requires_grad = False VGG_model_Adam.classifier._modules['6'] = nn.Linear(4096,2) VGG_model_Adam.classifier._modules['7'] = nn.LogSoftmax(dim=1) #将模型放到GPU上 VGG_model_SGD = VGG_model_SGD.to(device) VGG_model_Adam = VGG_model_Adam.to(device)#选择代价函数 costFunc = nn.NLLLoss() #选择优化器,注意只更改模型的最后一层的参数,激活函数没有参数 #这里选用了两个优化器SGD和Adam,以测试不同优化器的准确性 optim_SGD = torch.optim.SGD(VGG_model_SGD.classifier[6].parameters(), lr=0.001) optim_Adam = torch.optim.Adam(VGG_model_Adam.classifier[6].parameters(), lr=0.001) #训练部分 def train(model, loader, size, optimizer=None): #启用 BatchNormalization 和 Dropout model.train() corrects = 0 for inputs, labels in loader: #将数据放在GPU上,以后的计算都在GPU上以加快训练速度 inputs = inputs.to(device) labels = labels.to(device) #利用当前模型的参数对输入进行预测,得到当前预测的输出outputs outputs = model(inputs) #计算当前预测的结果与真实结果的误差,使用某种损失函数 loss = costFunc(outputs, labels) #将梯度清零 optimizer.zero_grad() #误差反向传播 loss.backward() #更新模型权值 optimizer.step() #计算正确率,用以与测试集数据做比较 index, predicts = torch.max(outputs.data,1) corrects += torch.sum(predicts == labels.data) acc = corrects.data.item()/size print('acc:', acc) print('SGD:') train(VGG_model_SGD, train_loader, size=len(train_set), optimizer=optim_SGD) print('Adam:') train(VGG_model_Adam, train_loader, size=len(train_set), optimizer=optim_Adam)#测试部分 def test_model(model, loader, size): #该句用以暂停参数更新,不然即使不进行训练,模型的参数也会更新 model.eval() correct_num = 0 #测试主要思想就是不断从loader中读取一batch(本程序中大小为40)的数据,然后使用该数据的输入通过模型得到输出, #然后使用该输出与数据的真实类别做比较,将预测正确的数据数量累加到某个变量中,最后用该变量除以数据集的大小, #就得到了预测的正确率 for inputs, labels in loader: inputs = inputs.to(device) labels = labels.to(device) outputs = model(inputs) indexs, predicts = torch.max(outputs.data, 1) correct_num += torch.sum(predicts == labels.data) #不加.data.item()会出现除法错误 acc = correct_num.data.item()/size #注意写法,与其他语言不同,字符串内{:.4f},不要忘记:,另外字符串结束后用的是.而不是, #还需要接一个format函数,该函数内可以写多个参数这些参数的数量与字符串内标记的将要输 #出的变量个数一致 print('acc:{:.4f}'.format(acc)) print('SGD:') #第二个参数传入的是loader,不是数据集set test_model(VGG_model_SGD, test_loader, len(test_set)) print('Adam:') test_model(VGG_model_Adam, test_loader, len(test_set))#测试数据为 SGD: acc:0.9760 Adam: acc:0.9805对不同的batch size训练数据进行统计,得到了如下的结果。
x = [5,10,20,30,40,50,60,70,80,90,100] y_SGD = [97.80,97.50,96.90,97.40,96.25,95.85,96.05,96.50,96.45,94.30,93.90] y_Adam = [97.45,97.70,98.00,98.15,98.35,97.85,97.65,97.85,98.05,97.65,97.50] plt.subplot(121) plt.plot(x,y_SGD) plt.xlabel('batch size') plt.ylabel('test acc') plt.title('SGD') plt.subplot(122) plt.plot(x,y_Adam) plt.xlabel('batch size') plt.title('Adam')下面我们对猫狗大战进行代码编写,这次使用比赛需要的训练集与测试集合。
由于所给的数据集没有结构化,我们将其中的cat,dog分类后重新上传到colab,而后解压缩。
! unzip "/content/drive/My Drive/lesson2/datasets/cat_dog.zip"接下来创建train_set和test_set
#创建训练集文件夹 train_set = datasets.ImageFolder('./cat_dog/train', transforms.Compose([ transforms.CenterCrop(224), transforms.ToTensor(), transforms.Normalize(mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225]), ])) #创建测试集文件夹 test_set = datasets.ImageFolder('./cat_dog/val', transforms.Compose([ transforms.CenterCrop(224), transforms.ToTensor(), transforms.Normalize(mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225]), ]))后面的代码与之前完全一致,最后我们可以得到结果。
-
-
展望学习
3.1 googLeNet Inception V1
-
googLeNet采用多层并联的方式,一层进行卷积、池化多种操作,对输出的几类通道归并为一个,当然,这要求输出图像的分辨率应该是一致的。
-
网络结构中添加了几个辅助的分类器以解决梯度消失问题
-
该网络没有多余的全连接层,参数量也并不多
-
主要指导思想为,不同的卷积核可以提供不同的信息,如果采用多种卷积核并行对图像进行处理,就可以保留足够多的信息特征描述图像,所以一层采用多种尺寸的卷积核(1×1,3×3,5×5),由于池化的存在,模型的通道数量会越来越大
-
增加1*1的卷积核对数据进行降维。由于参数量的计算公式为:
\[卷积层参数数量=(核长×核宽×输入通道数+单个卷积核偏置项数量(1))×核数 \] 简化则有:
\[卷积层参数数量=(核维度^2×输入通道数+1)×核数 \] 所以,如果减少输入通道数,那么就必然会降低卷积层参数数量,1*1的卷积核的参数数量为
\[Q=(1×1×输入通道数+1)×核数=(输入通道数+1)×核数 \] 对比通过1×1×较小的通道数的特征图来说,这种方式可以大大降低参数的数量
比如,如果某特征图输入为28×28×256,通过3×3×192的卷积核,padding为0,步长为1,那么参数数量为
\[Q=(3×3×256+1)×192=442560 \] 如果首先通过1×1×64的卷积核降维,而后再通过3×3×192的卷积核,那么参数减少为
\[Q_1=(1×1×256+1)×64=16448\\Map_{out}=((28-1)/1+1)^2×64=28×28×64\\Q_2=(3×3×64+1)×192=110784 \\Q_{all}=Q_1+Q_2=16448+110784=127232 \] 可见参数的减少是十分可观的。这样也加深了模型的深度,进而增加了激活函数的个数,提高了模型的非线性表达能力。
3.2 googLeNet Inception V2
-
Inception V3的主要改进是利用两个3×3的卷积核代替一个5×5的卷积核,如图所示
这样可以进一步降低参数数量,防止过拟合。另外,这样加深了模型的深度,进而增加了激活函数的个数,提高了模型的非线性表达能力。
假如输入为28×28×256,卷积核为5×5×192,改为两个3×3×192串联,padding为0,步长为1
\[Q_{5×5}=(5×5×256+1)×192=1228992\\ Q_{1_{3×3}}=(3×3×256+1)×192=442560\\ Map_{out}=((28-5)/1+1)^2×192=24×24×192\\ Q_{2_{3×3}}=(3×3×192+1)×192=331968\\ Q_{all_{3×3}}=442560+331968=774528 \]也可以大幅减少参数数量。
经过大量实践证明,两个3×3的卷积核串联和一个5×5的卷积核提取的特征效果大体一致
-
一般来说,缩小图像有两种方法,分别是池化→卷积和卷积→池化。前者会造成特征缺失,后者计算两比较大。所以googLeNet采用了并行方式进行处理。
3.3 googLeNet Inception V3
还进行了另外一种卷积分解,将3×3的卷积核用1×3和3×1两个卷积核来代替
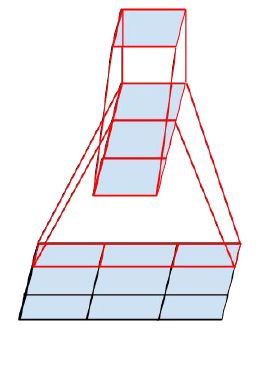
这种分解仅在中等大小的特征图上使用效果才比较好。(特征图大小12~20之间)
3.4 googLeNet Inception V4
- 引入了残差连接的方式。大大改善了梯度消失问题,大大加深了网络深度。还提升了训练速度和灵活性。
3.5 mobileNet
-
mobileNet的引入主要是为了在手机等小型终端进行学习任务,由于机能限制,必须降低模型的计算量和参数量。
-
该网络使用了depthwise separable convolution进行构建模型,depthwise separable convolution将标准卷积分解为了depthwise convolution和pointwise convolution,降低了模型计算复杂度
原来的计算复杂度模型为
\[D_K·D_K·M·N·D_F·D_F \]其中\(D_K×D_K\)为卷积核大小,\(M\)为输入通道数,\(N\)为输出通道数,\(D_F×D_F\)为特征图大小
经过分解后的计算复杂模型为
\[D_K·D_K·M·D_F·D_F \]这可以成倍降低模型计算复杂度
-
标准卷积可以表达为
\[G_{k,l,n}=\sum_{i,j,m}K_{i,j,m,n}·F_{k+i-1,l+j-1,m} \]其中\(i,j\)表示以\(k,l\)点临近的领域的点,在计算中要对这些点进行类似点积的操作(即乘权值后累加)
令\(i=0,j=0\),有\(k+i-1=k-1,l+j-1=l-1\) 。这也就是\((k,l)\)点左上角的像素点。
\(M\)为一个卷积核的层数,也是输入图像的通道数,\(m\)则是对\(M\)进行遍历的指示变量。\(N\)则是输出通道数。该式子的计算结果是一个通道的特征图。对\(N\)进行遍历,则得到所有的特征图。
进行分解后的depthwise convolution则为
\[\hat{G}_{k,l,m}=\sum_{i,j}\hat{K}_{i,j,m}·F_{k+i-1,l+j-1,m} \]与标准卷积相比,仅仅是去掉了对 \(m\) 的累加,取消了n的表示而已。也就是一个卷积核仅用于一个通道卷积的计算,标准卷积中,一个卷积核由多个卷积层构成,计算一次输出一个结果,该结果是分别计算卷积层之后的累加,还会增加偏置项。但depthwise convolution一个卷积核仅由一层卷积层构成,n个通道的图像通过n个卷积核计算之后输出n个特征图。
最后就是point convolution,他仅仅是将刚才输出的n个特征图进行卷积生成一个特征图而已。
-
这种分解后,复杂度仅为原来的
\[\frac{1}{N}+\frac{1}{D_K^2} \]参数含义同上所示
-
分解后还在两层都加入了BN层和ReLU函数,增加了模型的非线性表示能力
-
论文的第二个要点则是width multiplier和resolution multiplier,分别是用来成比例的减少通道数和分辨率所用
3.5 HybridSN
-
该模型的引入是为了解决高光谱图像HSI的特征提取问题,它不仅需要提取某个光谱内部的图像像素信息,还需要跨光谱进行特征提取。这方面的技术是3D卷积
-
2D卷积可以表示为
\[v_{i,j}^{x,y}=\phi(b_{i,j}+\sum_{\tau=1}^{d_{l-1}}\sum_{\rho=-\gamma}^{\gamma}\sum_{\sigma=-\delta}^{\delta}w_{i,j,\tau}^{\sigma,\rho}×v_{i-1,\tau}^{x+\sigma,y+\rho}) \]其中\(\sigma,\rho\)对\((x,y)\)点周围的像素点进行遍历以进行求和,卷积核的大小定义为\(2\gamma+1,2\delta+1\)。\(w\)为卷积核某点对应的权重。
\(\tau\) 的含义为输入图像的通道数和卷积核的层数,\(b_{i,j}\)为偏置项
这个公式还有几个点需要注意,第一点,\(i\) 应该代表的是输入层和输出层的关系,\(i-1\)应该表示的是当前所处的模型的层数(通俗的讲,也就是第几个卷积层), \(i\)指的是通过\(i-1\)层的输出作为第 \(i\) 层的输入,而后第\(i\)层应该产生什么样的输出。
这也就是论文中layer的含义。\(w\)下的 \(i\) 表示的是用第 \(i\) 层的卷积核进行计算。
第二点,应该明确输入应该是四维的,也就是
\[长×宽×通道数×特征图个数 \]这四个指标在公式中分别用 \(x,y,\tau,j\) 来表示,\(j\) 表示的应该是第几个特征图。
-
类似地,可以定义3D卷积
\[v_{i,j}^{x,y,z}=\phi(b_{i,j}+\sum_{\tau=1}^{d_{l-1}}\sum_{\lambda=-\eta}^{\eta}\sum_{\rho=-\gamma}^{\gamma}\sum_{\sigma=-\delta}^{\delta}w_{i,j,\tau}^{\sigma,\rho,\lambda}×v_{i-1,\tau}^{x+\sigma,y+\rho,z+\lambda}) \]理解了2D卷积,3D卷积仅仅是增加了一个新维度而已,\(2\eta+1\) 表征的是增加的第三个维度的卷积核的大小。在这里,第三个维度是光谱,其他应用中也可以是视频等。
-