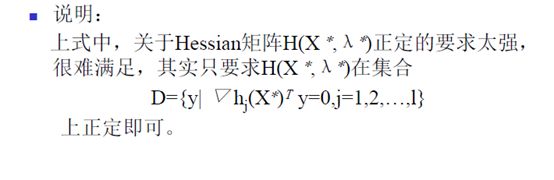优化理论基础

算是读书笔记，记录一下。没有证明，只有定理。

一、最优化数学基础

1正定矩阵

1 正定矩阵定义

对应着半正定矩阵，负定矩阵，半负定矩阵和不定矩阵，这里只以正定矩阵为例。

 

则A为正定矩阵。

定义是一种常用的，用来判定某个对称矩阵是否是正定矩阵的方法。

2 正定矩阵的判定方法

（1）根据定义判断

（2）根据矩阵的顺序主子式判断

（3）根据矩阵的特征值判断

 

3 扩充知识点

（1）判定正定矩阵的第一种方法，定义。需要计算行向量乘矩阵乘列向量，了解矩阵的乘法，理清维度和最终返回的结果的维度。

（2）计算顺序主子式，就是计算不同阶数的行列式值。了解行列式的有关概念和性质；高阶行列式展开计算的方法，某一行或者某一列的元素乘以对应的代数余子式之和。

（3）矩阵的特征值。特征值的计算，根据定义，求解特征多项式的解。一个解就是一个特征值。根据特征值计算对应的特征向量，每个特征值都拥有基础解系，一重特征值在求解特征多项式过程中对应的维数为一，基础解系维度为一，三者一一对应。

（4）实对称矩阵。常用的，特殊的，很重要的一个矩阵。拥有很多优良性质。不同的特征值对应的特征向量相互正交，同一个特征值对应的解系里的特征向量不一定正交，可以通过施密特正交化转换成正交的。实对称矩阵A，存在正交矩阵Q，使得Q-1AQ=QTAQ为对角型矩阵，对角线上的元素即为特征值。Q特征值对应的特征向量正交化，归一化后，合并在一起的矩阵。

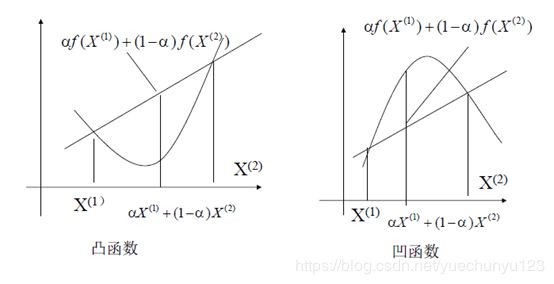
2 函数的凹凸性

1 区分凹函数和凸函数。求最小值是凸，最大值是凹。以凸函数为例。

 

2 凸函数的判定

（1）性质来判定

自变量线性组合对应的函数值小于等于自变量函数值对应的线性组合。

 

（2）一阶充要条件

 

（3）二阶充要条件

 

需要判定海瑟矩阵是否为半正定，用到第一部分的判定方法。

3 极值的性质

极值有极大值和极小值，此处以极小值为例

1 极值点的一阶必要条件

极值点处的梯度为0，必要条件，反过来不成立。

 

2 极值点的二阶必要条件

极值点处的梯度（各向偏导）为0，海瑟矩阵半正定。

是必要条件，反过来不成立。

 

反过来不成立的例子：

 

 

3 极值点的二阶充分条件

用来判定是否为极值点

 

先求出驻点，然后判断驻点处的海瑟矩阵是否为正定。

当驻点出的海瑟矩阵半正定时，通过放松后的条件判断。

放松后的二阶充分条件：局部区域内半正定（局部凸函数）

 

举例：

 

4 极值的二阶充要条件

凸函数的驻点为全局极值点

 

总结：

 

二、无约束优化

此处以求极小值为例，极大值情况相同。某些情况（现实中大多数情况）

1 一阶导数（梯度下降法）

如果梯度存在，梯度方向是函数值上升最快的方向，反方向是下降最快的方向，使用梯度反方向作迭代的方向，并使用一维搜索求解步长，进行迭代。

 

2 二阶导数（牛顿法）

1 牛顿法

最简单的牛顿法，利用极值的一阶必要条件（驻点，梯度，各向导数为0），将函数表达式在Xn出泰勒展开到二阶，求出Xn+1的迭代公式。

 

 

如果原函数为正定二次函数，则通过牛顿法，在牛顿方向，以步长为一，迭代一次便可到达极小值点。

缺点一：牛顿方向可能不是下降的方向，步长选的不好，可能不会收敛。

 

缺点二：牛顿方向需要求海瑟矩阵的逆，占用内存，对于不可逆的情况，算法不能进行。

 

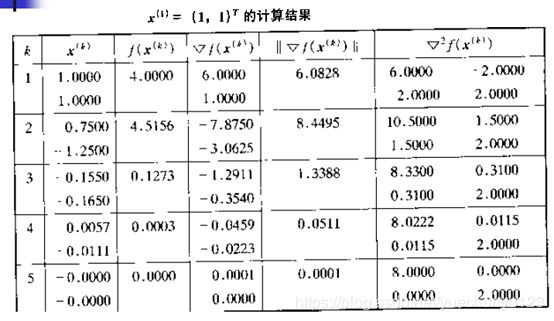
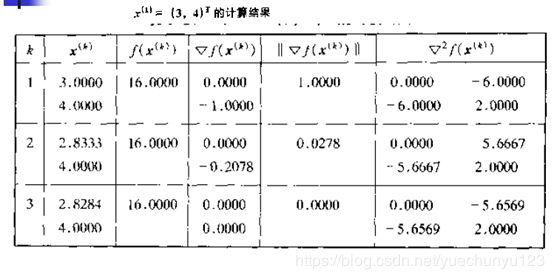
牛顿法缺点的例子：

第一个点，函数值慢慢减小；第二个点，函数值不变，体现缺点一；第三个点，海瑟矩阵奇异，不可求逆，体现缺点二。

2 阻尼牛顿法

针对缺点一，阻尼牛顿法在牛顿方向上，使用一维搜索，寻找一个使函数值下降最快的步长。

3 拟牛顿法

针对缺点二，构造一个正定矩阵（正定矩阵可以求逆，并保持较快的下降速度），代替海瑟矩阵，再求出拟牛顿方向，进行迭代。每次迭代中，使用当前点的信息，迭代正定矩阵，计算拟牛顿方向，一维搜索确定步长。

DFP拟牛顿算法，每次更新的是海瑟矩阵的逆，BFGS更新的是海瑟矩阵。

 

三、有约束优化

1 只有等式约束

1 一阶必要条件，拉格朗日定理

最优解处的函数的梯度可以由每个约束的梯度线性表示。拉格朗日函数对各个方向的偏导为0，加上原来的等式约束，可以写出所有的等式，求解出X和λ。

2 二阶充分条件，用来判断是否为极值点

通过约束驻点的海瑟矩阵来判断。

二阶充分条件的放松条件：

在约束的梯度垂直面上正定即可。

例子：

2 只有不等式约束

1 KKT必要条件

最优解在不等式表面时，最优解处的梯度可以由不等式的梯度线性表示，且在不等梯度的正方向上。

相对于等式，多了个系数u大于等于0和乘积等于0的式子，再加上越来不等式的约束，由以上所有的式子解出可能的约束驻点。

2 KKT充分条件，判断是否为极值点

目标和约束都为凸函数，满足KKT条件，则为全局最优解。

3 混合约束

1 KKT必要条件

局部最优解处的梯度可以由等式和不等式约束的梯度线性表示，且不等式为梯度的正方向，不等式和系数乘积为0。

2 KKT充要条件

3 拉格朗日对偶

如果满足KKT充要条件（两凸加上仿射函数，就是线性函数），则最优解处满足KKT条件，且原问题和对偶问题符合强对偶性。