拉格朗日乘子法（Lagrange multiplier）

问题提出

已知函数 z=f(x,y) (本文假设它是凸函数，三维空间想象成抛物体，局部极值就是全域唯一极值)，现在要求

minf(x,y) 只需求解方程组：

⎧⎩⎨⎪⎪⎪⎪∂f∂x=0∂f∂y=0

上述为无约束问题。但实际存在一个或多个约束条件，如 g(x,y)=0 ，这时应该怎么办呢？

拉格朗日乘子法

思路与直观

约束条件

g(x,y)=0 或者 g(x,y)=C ，考虑三维空间，h是一个曲面，投影到二维是一条曲线，为了直观表达我们考虑h是x和y的线性组合即h是一个平面，和xoy相交与一条直线
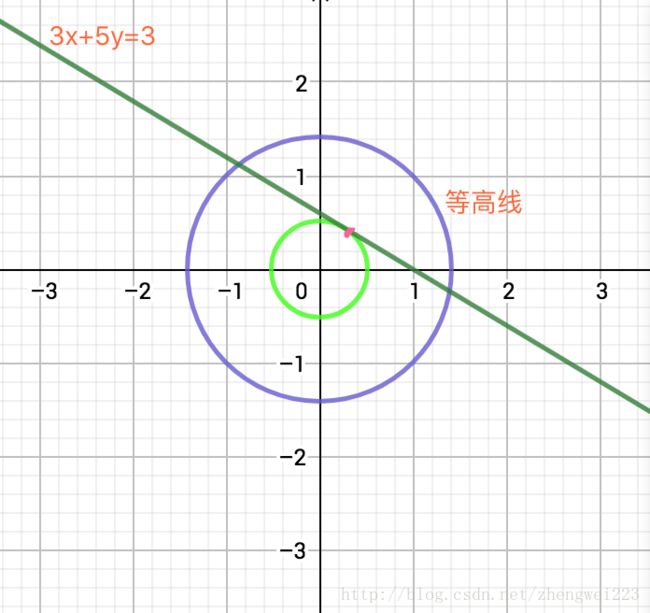
g(x,y):3x+5y=3

目标函数
考虑目标函数 f=x2+y2 即抛物面，它们的三维图像：

现在我们做 f(x,y) 的等高线，可以在平面上作出无限个同心圆，显然，等高线与h在平面上的投影的相交点都是二函数联立的解，但现在我们求的是极值，那么只有一种特殊的交点是唯一解：

维基百科上是这张图：

虚线是等高线，红线是约束线，交点就是同时满足等式约束条件和目标函数的可行域的值，但肯定不是最优值，因为相交意味着肯定还存在其它的等高线在该条等高线的内部或者外部，使得新的等高线与目标函数的交点的值更大或者更小，只有到等高线与目标函数的曲线相切的时候，可能取得最优值。

回到我们的例子，我们当然可以用几何解法求出同心圆（绿色）和直线（深绿）切点的坐标（9/34，15/34），但是怎么推广为一般形式的解法呢？

形式化

如图所示，等高线和目标函数的曲线在该点（极值点）的法向量必须有相同方向，最优值求解即寻找 λ ,使得 ▽x,yf=−λ▽x,yg ， λ 是常数。

拉格朗日函数也就写作： Lp=f(x,y)+λg(x,y) ， λ 称为拉格朗日算子。
此式分别对自变量和 λ 求导，联立解方程得极值点。

根据这个方法，我们验算一下一开始的例子：
1、首先写出拉格朗日函数： L=x2+y2+λ(3x+5y−3)
2、偏微分方程组

⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪∂L∂x=2x+3λ=0∂L∂y=2x+5λ=0∂L∂λ=3x+5y−3=0

3、求解 λ=−6/34,x=9/34,y=15/34
与我们作图几何求解结果一致。

其他情况

1.多变量单约束（等值）

我们可通过解下式获得最优解:
∇x1,...,xn,λL(x1,...,xn,λ)=0

2.多约束

L(x1,...,xn,λ1,...,λM)=f(x1,..,xn)−∑k=1Mλkgk(x1,...,xn)

解：

∇x1,...,xn,λ1,...,λML(x1,...,xn,λ1,...,λM)=0

拉格朗日对偶性、不等式约束与KKT

摘自《统计学习方法》

在约束最优化问题中，常常利用拉格朗日对偶性将原始问题转化为对偶问题。通过解对偶问题而得到原始问题的解.

1. 原始问题(primal problem)

假设 f(x),ci(x),hj(x) 是定义在 Rn 上的连续可微函数。考虑如下最优化问题：

minf(x) ………………………………………… (1)

s.t.ci(x)≤0,i=1,2,...,k …………………… (2)

hj(x)=0,j=1,2,...,l …………………………(3)

称此约束最优化问题为原始最优化问题或原始问题.
引入广义拉格朗日函数 ：
L(x,α,β)=f(x)+∑ki=1αici(x)+∑lj=1βjhj(x) …… (4)
这里, αi,βj 是拉格朗日乘子，特别要求 αi≥0 . 如果把 L(x,α,β) 看做是α,β的函数（把x看做常数），然后求最大值，可以证明这个最大值（实际是一个函数）它与f(x)等价。
经过我们优化（不要管什么方法），就是求α,β的值使得 L(x,α,β) 取得最大值（此过程中把x看做常量），一旦求出， maxL(x,α,β) 就是只和x有关的函数，定义这个函数为：

θP(x)=maxα,β;αi>0L(x,α,β)=maxα,β;αi>0[f(x)+∑i=1kαici(x)+∑j=1lβjhj(x)](5)

这里下标P表示原始问题.
一定记住，求极值之前max里面是α,β的函数，求极值后max外面是关于x的函数。
下面我们以x是否满足约束条件两方面来分析这个函数:
A.确定一个x违反约束即c(x)>0或者h(x)≠0，这时极大值是正无穷
θP(x)=+∞(6) ，f(x)是常量,c(x)是大于0的常量，h(x)是不为0的常量，要求α,β使得三项相加最大，这是没有顶的
B.x满足原始的约束，则 θP(x)=f(x) ，f(x)就是个常量，c(x)是小于等于0的常量，最大值就是f(x)了.

ΘP(x)={=f(x)=+∞x满足约束条件其他(7)

所以在约束条件下，
minxf(x)=minxθP(x)=minxmaxα,β;αi≥0L(x,α,β)(8)
它与原始问题（1）~（3）是等价的，它们有同样的解。
问题（8）称为广义拉格朗日函数的极小极大问题.

这样一来，就把原始最优化问题表示为广义拉格朗日函数的极小极大问题。为了方便，定义原始问题的最优值
p∗=minxf(x)=minxθP(x)(9)
称为原始问题的值（值不是解，值是函数极值，解是未知数的取值）.

2. 对偶问题(dual problem)

定义

θD(α,β)=minxL(x,α,β)(10)
这次把α,β看做常量，求x使得L(x,α,β)最小后，它是α,β的函数。
再考虑极大化上式，即求解α,β使式(10)最大
maxα,β;αi≥0θD(α,β)=maxα,β;αi≥0minxL(x,α,β)(11)

称为原使问题的对偶问题.
形式上可以看出很对称，只不过原始问题是先固定L(x,α,β)中的x，优化出参数α,β，再优化最优x，而对偶问题是先固定α,β，优化出最优x，然后再确定参数α,β.——得到最大最小值其实不是重点，解出x,α,β才是重点。
定义对偶问题的最优值
d∗=maxα,β;αi≥0θD(α,β) ……………………………………………… (12)

称为对偶问题的值.

3. 原始问题和对偶问题的关系

这里直接列出《统计学习方法》中的几个定理和推论.
定理1 若原始问题和对偶问题都有最优值，则

d∗=maxα,β;αi≥0minxL(x,α,β)≤minxmaxα,β;αi≥0L(x,α,β)=p∗(13)

推论1 设x∗和α∗,β∗分别是原始问题(公式1~3)和对偶问题(公式11)的可行解，并且d∗=p∗，则 x∗和α∗,β∗分别是原始问题和对偶问题的最优解.
——极值相同，解共享
反过来说——如果你可以证明这两个问题的解是一致的，那么任何一种解法解出的xαβ都是可以的。但是到底满足什么样的条件才能使d∗=p∗呢？

定理2 考虑原始问题(公式1~3)和对偶问题(式11). 假设函数f(x)和 ci(x) 是凸函数, hj(x) 是仿射函数(即由一阶多项式构成的函数，f(x)=Ax + b, A是矩阵，x，b是向量); 并且假设不等式约束 ci(x) 是严格可行的, 即存在x, 对所有i有 ci(x) <0, 则**存在**x∗,α∗,β∗，使x∗是原始问题的解, α∗,β∗是对偶问题的解，并且：

p∗=d∗=L(x∗,α∗,β∗)

——一句话（实际上很多条件：f，c是凸的，h是仿的，c是严格的）这样的解是存在的
——解存在，什么样的解是这个存在的解呢？

定理3 对原始问题(公式1~3)和对偶问题(公式11), 假设函数f(x)和 ci(x) 是凸函数， hj(x) 是仿射函数；并且假设不等式约束 ci(x) 是严格可行的, 则x∗和α∗,β∗分别是原始问题和对偶问题的解的充分必要条件是x∗,α∗,β∗满足下面的KKT（Karush-Kuhn-Tucker卡罗需-库恩-塔克）条件：
——一句话，下面的方程组解出来的x∗,α∗,β∗就是原始问题和对偶问题的解

∇xL(x∗,α∗,β∗)=0

∇αL(x∗,α∗,β∗)=0

∇βL(x∗,α∗,β∗)=0

-###################三偏导为0，好理解#####################-

α∗ici(x∗)=0,i=1,2,...,k……………………（对偶互补条件）

ci(x∗)≤0,i=1,2,...,k(原始约束)

α∗i≥0,i=1,2,...,k(原始约束)

hj(x∗)=0,j=1,2,...,l(原始约束)

前面三个条件是由解析函数的知识，对于各个变量的偏导数为0（这就解释了一开始为什么假设三个函数连续可微，如果不连续可微的话，这里的偏导数存不存在就不能保证）
第四个条件，对偶互补条件是一种严格的条件，满足它，对偶就是强对偶。
也就是说，只有强对偶，它们的解才是等价的。

特别注意，若 α∗i>0 ，则必有 ci(x∗)=0 ，这个知识点会在 SVM 的推导中用到.

理解与帮助

拉格朗日乘子法的基本形式可以帮助我们找出约束条件下的极值点；
其扩展形式可以帮助我们在多约束条件下找到极值点；

一个比较棘手的问题是，约束条件可能是不等式，在这种情况下我们先考虑原问题的等价形式——广义拉格朗日极小极大问题。

但是这个等价形式没什么用，原问题在原地踏步，让我们看到希望的是，可以写出广义拉格朗日极小极大问题的对偶问题——拉格朗日极大极小问题（这名字多写几次感觉高大上）

这是一个新问题，它的解表示为 d∗ ，当然它和原问题不是等价的，有 d∗≤p∗ 。这在直观上也不难理解，所有最大值中最小的一个（min max L） 也要大于或等于 最小值中最大的那个（max min L）！

这个式子

maxα,β;αi≥0minxL(x,α,β)=maxα,β;αi≥0minx⎧⎩⎨⎪⎪f(x)+∑i=1kαici(x)+∑j=1lβjhj(x)⎫⎭⎬⎪⎪

据说，这个式子比原问题更好解。在满足某些条件的情况下，解对偶问题就解出了原问题。

某些条件指的就是，KKT条件。KKT宣称满足KKT条件，原问题和对偶问题同解，反过来要想二问题同解必须满足KKT条件。意义：它是一个非线性规划（Nonlinear Programming）问题能有最优化解法的必要和充分条件。
说它是条件，也可以说它是方程组，解出这个方程组就同时解出了原始问题与对偶问题。

KKT的直观理解

请参考非线性优化中的KKT条件该如何理解？ - 知乎

What is an intuitive explanation of the KKT conditions?