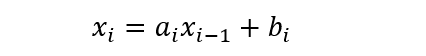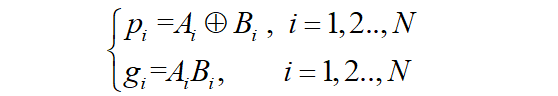【HDL系列】Kogge-Stone加法器原理与设计
目录
一、Kogge-Stone并行算法
二、Kogge-Stone加法器
三、Verilog设计
Kogge-Stone加法器是利用Peter M. Kogge和Harold S.Stone于1972年提出的一种并行算法生成的一种树形加法器。
一、Kogge-Stone并行算法
Kogge和Stone根据一般m阶递归问题提出一种并行算法。本文介绍其一阶递归问题的并行结构，详细请阅读其论文。
对于序列X1,X2,X3,…,Xn，其中Xi是其之前m个数的函数，也就是:
以上是一个常见的问题，如线性时变系统，对于i时刻的Xi，可由下式计算而来：
其中Ai和Bi表示系统内部动态系数，可为实数或者复数，常量，时变矩阵等。
使用简化的并行算法解决以下一阶递归问题，给定X1=b1,则
为解决如上问题，论文中定义了下式：
其中对ar系数使用的是连乘符合，之后与bj相乘后使用的是累积和符号。
所以，
上式又可以重新写成如下形式：
其一般形式为：
Q(i,1)和 Q(2i,i+1)可以独立计算，Q(i,1)和Q(2i,i+1)又可以单独分解独立计算，每个层级都可以独立计算，因此加快了运算速度。以下是x8的计算图例。
x8计算示意图
X1至X8的计算步骤、系数与公式，来源Kogge-Stone论文
上图为x1-x8的计算步骤，系数和公式，分三个时间步骤完成：
T=0：输入系数b1-b7
T=1：根据其对应的a1-a8系数计算相邻两项
T=2：再次根据算式合并Q值
根据以上x1至x8的计算方式，画出其图例如下，如果看过本号之前的文章，相信你对此结构已经非常熟悉：
X1至X8的计算图示
二、Kogge-Stone加法器
基于以上介绍的Kogge-Stone的一阶递归问题的并行结构，如何应用到加法器中呢？我们先回顾下超前进位加法器中进位链的计算。
对于N比特的A和B两数，结果为N比特S和1比特进位Cout，超前进位加法器的进位链与和公式的计算公式如下：
其中：
重点关注进位链ci的生成算式，发现其属于Kogge-Stone概括的一阶递归问题：
所以ci算式写成Kogge-Stone形式：
所以，如对于C1-C4等的生成，其算式如下：
根据以上原理，8比特的加法器进位链并行计算的Kogge-Stone形式的树形结构如下图所示：
8位加法器进位链Ci生成树形图
三、Verilog设计
设计一个16比特的Kogge-Stone加法器，分三部分：
（1）生成g，p信号，由半加器模块组成；
（2）每个节点处理单元实现，即每个节点中的系数生成和每个独立的Q值计算；
（3）生成输出进位Cout和S信号。
该16比特Kogge-Stone位加法器进位链的树形结构如下图所示：
16位加法器进位链生成树形图
从图中足以见Kogge-Stone结构加法器布线尤其拥塞，但其好处在于进位链生成的延迟单位少。在verilog中根据其规律使用generate和endgenerate语句生成各级信号如下。
16比特Kogge-Stone加法器PG生成逻辑
16比特Kogge-Stone加法器level1生成逻辑
16比特Kogge-Stone加法器level2生成逻辑
16比特Kogge-Stone加法器level3生成逻辑
16比特Kogge-Stone加法器level4生成逻辑
16比特Kogge-Stone加法器和S生成逻辑
欢迎批评指正，更多阅读，关注“纸上谈芯”，不定期更新，共同学习:
