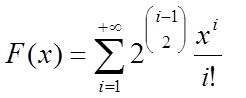2019 HL暑假集训 Day2
本次考试未参加,因而没有心路历程
题目按难度从简到难手动排序————题记
T1. 小刚传说 (legendary.cpp/c/pas)
【 问题描述】:
众所周知, 刘小刚是海亮中学的金牌教练, 然而世人并不知道他的传奇经历, 以及那个曾经轰动世界的名字 sharpland.
2003 年, 美国研究团队在量子计算机的研制上取得了重大突破, 一旦美国成功研发出量子计算机, 一切加密手段都将形同虚设。 当此之时, 国内第一黑客 sharpland 秘密潜入美国中央情报局, 得知关于量子计算机的研究成果封存于五角大楼计算机群之中。 经过一周的0Day 挖掘, sharpland 成功侵入计算机群, 却发现这里的文件保护机制非同寻常。
五角大楼计算机群的文件形成了树结构, 且树的形态随时间变化。 已知初始时刻树上仅有一个根节点 1, 当成功拷贝结点 i 上的文件时, 树上会新增结点 i+1, 它的父亲为一个已存在的结点。 树的大小增加为 n 时便会停止。
sharpland 通过之前挖掘的 0Day 成功推算出了所有新增结点的父亲, 为了破解文件保护系统, 他需要在每次新增结点后新增的结点 i 和上一次新增的结点 i-1 的路径长度。
【 输入格式】:
第一行, 一个整数 n n n 表示最终树的大小。
接下来 n − 1 n-1 n−1 行, 每行一个整数表示新增节点的父亲。
【 输出格式】:
共 n − 1 n-1 n−1 行, 每行一个整数表示答案。
【 输入输出样例 1】:
I n p u t Input Input:
6
1
2
2
1
5
O u t p u t Output Output:
1
1
2
3
1
【 时空限制】:
时间限制: 2 s 2s 2s
空间限制: 256 M B 256MB 256MB
【 数据范围】
对于 30%的数据, n < = 100 n <= 100 n<=100
对于 60%的数据, n < = 2000 n <= 2000 n<=2000
对于 100%的数据, 2 < = n < = 200000 2 <= n <= 200000 2<=n<=200000
【 后记】:
sharpland 成功窃取数据的那一刻, 中央情报局察觉到了数据失窃并发布全球通缉令,sharpland 隐姓埋名逃会国内, 以刘小刚为化名, 以高中竞赛教练为掩护, 生活至今。 然而第一黑客 sharpland 之名早已响彻世界。
正解:
树上两点 A , B A,B A,B的距离就是
![]()
每次求出 LCA 就可以了
正解代码:
#include
if (l==fa[0][x]) continue;
fa[0][l]=x;
dfs(l,y+1);
}
}
void init()
{
dfs(root,0);
for (int i=1;(1<<i)<n;i++)
for (int j=1;j<=n;j++)
if (fa[i-1][j] < 0) fa[i][j]=-1;
else fa[i][j]=fa[i-1][fa[i-1][j]];
}
inline int lca(int u,int v)
{
if (dep[u]>dep[v]) swap(u,v);
for (int i=0,d=dep[v]-dep[u];d;i++,d>>=1)
if (d&1) v=fa[i][v];
if (u==v) return u;
for (int i=25;i>=0;i--)
if (fa[i][v]!=fa[i][u])
{
v=fa[i][v];
u=fa[i][u];
}
return fa[0][u];
}
int main()
{
freopen("legendary.in","r",stdin);
freopen("legendary.out","w",stdout);
memset(vis,0,sizeof(vis));
memset(fa,0,sizeof(fa));
memset(a,0,sizeof(a));
memset(dep,0,sizeof(dep));
memset(head,0,sizeof(head));
tot = 0;
scanf("%d",&n);
s[0] = 1;
for (int i=1;i<n;i++) {
int x;
scanf("%d",&x);
s[i] = s[i-1] + 1;
insert(s[i], x), insert(x, s[i]);
}
fa[0][root] = -1;
init();
for (int i=1;i<n;i++)
printf("%d\n", dep[s[i]]+dep[s[i-1]]-2*dep[lca(s[i], s[i-1])]);
return 0;
}
/*
6 1 2 2 1 5
*/
T2. 中珂院的难题(kotori.cpp/c/pas)
【 问题描述】:
“ 我已经无法获得幸福了, 因为我发觉, 我早已是幸福的人了。 ” ——珂朵莉
近日, 中国珂学院的研究员们遇到了一个难题, 他们手上有一个数列 a n a_n an , 现在有 m m m 次操作, 每次操作有三个参数 l , r , k l, r, k l,r,k ,表示选取一个区间 [ l , r ] [l,r] [l,r], 对于区间中的每个元素 a n a_n an 把它加上一个组合数 , 求 m 次操作后得到的数列, 答案对 1 0 9 + 7 10^9+7 109+7 取模。
“ 要是我们中有 OI 选手在就好了” 一位研究员如是说, 于是他们找到了身为 OI 选手
的你, 希望你能帮助他们解决这个问题。
【 输入格式】:
第一行, 两个整数 n , m n,m n,m。
接下来 m m m 行, 每行 3 个整数 l , r , k l,r,k l,r,k 表示一次操作。
【 输出格式】:
一行 n 个整数表示操作结束后的数列, 答案对 1 e 9 + 7 1e9 + 7 1e9+7 取模。
【 输入输出样例 1】:
I n p u t 1 Input1 Input1:
5 1
0 0 0 0 0
1 5 0
O u t p u t 1 Output1 Output1:
1 1 1 1 1
【 输入输出样例 2】:
I n p u t 2 Input2 Input2:
10 2
1 2 3 4 5 0 0 0 0 0
1 6 1
6 10 2
O u p u t 2 Ouput2 Ouput2:
2 4 6 8 10 7 3 6 10 15
【 数据范围】:
对于 50%的数据, n , m < = 2000 , k < = 100 n, m <=2000, k <= 100 n,m<=2000,k<=100
对于 100%的数据, n , m < = 105 , k < = 100 n, m <= 105, k <= 100 n,m<=105,k<=100
【 时空限制】:
时间限制: 2 s 2s 2s
空间限制: 256 M B 256MB 256MB
正解:
我们知道这样的组合数序列进行 k + 1 k+1 k+1阶差分之后全部变为 0 0 0
按照差分模板,我们每次在第 k + 1 k+1 k+1 层差分的 l l l 位置加上 1 1 1
然后处理一下 1 1 1~ ( k + 1 ) (k+1) (k+1) 的 r + 1 r+1 r+1 位置,消去前缀和对后面的影响 c h ch ch
也就是在第 j j j 层差分的 r + 1 r+1 r+1 位置减去前面的前缀和
求出这个前缀和的值需要一些观察—— c y q cyq cyq
正解代码:
#includeT3. 欧拉图(euler.cpp/c/pas)
【 问题描述】:
递推树上递推果, 递推树下你和我。 递推树前做游戏, 递推树后做交易。
欧拉图指的是拥有欧拉回路的图, 也就是说一个图是欧拉图需要满足图是连通的, 且所有点的度数为偶数。 图中不能有重边和自环。
求 n n n 个点的有标号欧拉图有多少个, 两个欧拉图不同, 当且仅当存在边集不同。
答案对 998244353 998244353 998244353 取模。
【 输入格式】:
一个整数 n n n。
【 输出格式】:
一个整数表示答案, 答案对 998244353 998244353 998244353 取模。
【 输入输出样例 1】:
I n p u t 1 Input1 Input1:
5
O u t p u t 1 Output1 Output1:
46050276
【 输入输出样例 2】:
I n p u t 2 Input2 Input2:
506
O u t p u t 2 Output2 Output2:
38
【 数据范围】:
对于 20% 的数据, n ≤ 10 n≤10 n≤10
对于 60% 的数据, n ≤ 2000 n≤2000 n≤2000
对于 100% 的数据, n ≤ 1 0 5 n≤10^5 n≤105
数据纯手工构造, 有梯度
【 时空限制】:
时间限制: 2 s 2s 2s
空间限制: 512 M B 512MB 512MB
然后利用有标号集合计数的方法写出欧拉图的生成函数: G ( x ) G(x) G(x) = = = I n In In F ( x ) F(x) F(x)
维护一波多项式操作就可以了
正解代码:
//代码 by syq, 反正我是没看懂
#include