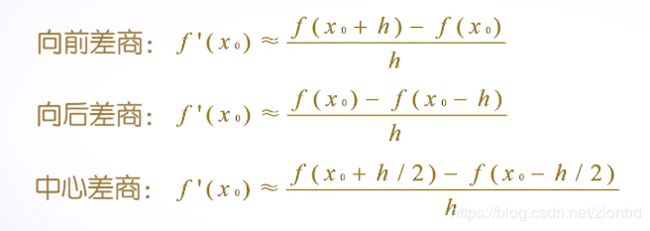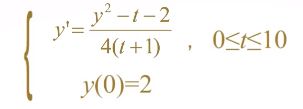六、数值微积分与方程求解(MATLAB学习笔记)
六、数值微积分与方程求解
6.1 数值微分与数值积分★
高等数学是解析解,MATLAB求数值解。
6.1.1 数值差分与差商:
6.1.2 数值微分的实现:
向前差分函数diff(),计算向量元素间差分。调用方法:
diff(x,n):计算向量x的n阶向前差分。(一阶:dx(i)=x(i+1)-x(i))diff(A,n,dim):计算矩阵A的n阶差分,(默认)dim=1,按列计算。
6.1.3 数值积分
可用牛顿-莱布尼茨公式计算。若无法求原函数,可用MATLAB实现:
- 基于自适应的辛普森方法:
[l,n]=quad(filename,a,b,tol,trace) - 基于自适应Gauss-Labatto方法:
[l,n]=quadl(filename,a,b,tol,trace) - 基于全局自适应积分方法:
I=intergral(filename,a,b)(可求无穷积分) - 基于高斯-克朗罗德方法:
[l,err]=quadgk(filename,a,b)(求震荡函数积分,上下限可为无穷,可复数)
其中filename为被积函数名,被积函数可用函数句柄形式,a,b为定积分上下限,tol控制积分精度默认为e-6。trace控制是否展现积分过程,默认trace-0不展现。返回参数I为定积分的值,n为被积函数的调用次数。
基于梯形积分法:I=trapz(x,y),y=f(x).x和y为向量。
6.2 线性方程组求解★
直接法:以矩阵初等变换为基础,可以求得方程组的精确解,占用的内存空间大,一般适合求解低阶稠密线性方程组。
-
利用左除运算符‘\’,
x=A\b. -
LU分解提高运算速度,MATLABLU分解函数
[L,U]=lu(A),[L,U,P]=lu(A)[L,U,P]=lu(A); //PAx==Pb,PA==LU x=U\(L\P*b)
迭代解法:给定初值,逐步逼近,占用空间小,程序设计简单,适用于大型稀疏矩阵线性方程组,要考虑算法收敛性。
-
雅可比迭代法,Jacobi.m:
function[y,n]=jacobi(A,b,x0,ep)//系数矩阵,右端项,初值,精度 D=diag(diag(A)) L=-tril(A,-1); U=-trilu(A,1); B=D\(L+U); f=D\b; y=B*x0+f; n=1; while norm(y-x0)>=ep xo=y; y=B*x0+f; n=n+1; end
6.4 非线性方程求解与函数极值计算
单变量非线性方程求解:x=fzero(filename,x0),x0为迭代初始值。需作图检验。
非线性方程组求解:x=fsolve(filename,x0,option)
无约束最优化问题:x1,x2为左右区间,x0为初值
[xmin,fmin]=fminbnd(filename,x1,x2,option)[xmin,fmin]=fminsearch(filename,x0,option)
有约束最优化问题:变量在满足某约束条件下的最优化,约束条件有线性\非线性不等式\等式约束,x的上下界。求解函数:
[xmin,fmin]=fmincon(filename,x0,A,b,Aeq,beq,Lbnd,Ubnd,NonF,option)
Aeq,beq,Lbnd,Ubnd分别为线性不等式、线性等式、上下界约束,不存在用空矩阵表示。
6.5 常微分方程数值求解
凡含有参数,未知函数和未知函数导数 (或微分) 的方程,称为微分方程,有时简称为方程,未知函数是一元函数的微分方程称作常微分方程,未知函数是多元函数的微分方程称作偏微分方程。微分方程中出现的未知函数最高阶导数的阶数,称为微分方程的阶。数学理论参考:CSDN: 常微分方程 笔记

dsolve('eqn1','eqn2',...,'cond1','cond2',...,'var')函数:dsolve函数用于求常微分方程组的精确解,也称为常微分方程的符号解。如果没有初始条件或边界条件,则求出通解;如果有,则求出特解。eqni表示方程,condi表示初值,var表示微分方程中的自变量,系统默认为t。D为微分符号,D2表示二阶微分,D3表示三阶微分。使用参考:matlab求解常微分方程(组)—dsolve、ode系列函数详解(含例程)、matlab中微分方程的求解
常微分方程数值求解一般函数调用格式为[t,y]=solver(filename,tspan,y0,option)。t和y分别为列向量时间点和相应的数值解,filename为定义为f(t,y)且返回列向量的函数名,tspan为[t0,tf]表示求解区间,y0是初始状态向量,option为可选参数(相对误差、绝对误差等)。
常微分方程数值求解函数的统一命名格式:odennxx。ode是Ordinary Differential Equation缩写,nn是阶数数字,xx是算法的专门特征。
f=@(t,y)(y^2-t-2)/(4*(t+1));
[t,y]=ode23(f,[0,10],2);
y = deval(sol,x) 和 y = deval(x,sol) 可以计算 x 中包含的点处的微分方程结构体sol问题的解。
对于高阶方程需要转化为一阶常微分方程组,即状态方程。参考matlab求解常微分方程(组)—dsolve、ode系列函数详解(含例程)
系统的时间响应曲线是个啥???看不懂
相平面图:对于如下形式的二阶系统: 式中x是状态变量,可以是输出量,也可以不是输出量;它的解析函数,可以是线性的,也可以是非线性。若以 x(t)为横坐标,x’(t) 为纵坐标的直角坐标平面,由所有相轨迹组成的曲线族构成的图称为相平面图。
刚性问题:有一类常微分方程,其解的分量有的变化很快,有的变化很慢,且相差悬殊,这就是刚性问题(Stiff),非刚性方法计算较慢。选择以s结尾的函数,如ode15s。
| 求解器solver | 功能 | 说明 |
|---|---|---|
| ode45 | 一步算法:4、5阶龙格库塔方程:累计截断误差(Δx)^5 | 大部分尝试的首选算法 |
| ode23 | 一步算法:2、3阶龙格库塔方程:累计截断误差(Δx)^3 | 适用于精度较低的情形 |
| ode23t | 梯形算法 | 适度刚性情形 |
| ode15s | 多步法:Gear’s反向数值微分:精度中等 | 若ode45失效时,可以尝试使用 |
6.6 常微分方程应用举例
lamda=0.01;
f=@(t,x)[2*x(1)-lamda*x(1)*x(2);-x(2)+lamda*x(1)*x(2)];
[T,y]=ode23(f,[0,30],[300,150]);
plot(T,y(:,1),'-r',T,y(:,2),'-k')
plot(y(:,1),y(:,2))%相平面图