【鲁棒优化论文学习】Scarf上界的一个推广(Distribution-free Inventory Risk Pooling in a Multi-location Newsvendor)

1. Scarf上界的一个推广

这里worst-case分布之所以是“6点分布”，就在于每个 $(\cdot {)}^{+}$ 可以拆成两种情况，一共3个 $(\cdot {)}^{+}$，进而给出六点分布。

2. 证明技巧

首先，通过简单的对偶，问题可以写为：（均值 $m_1,m_2$、方差 ${\sigma }_1,{\sigma }_2$为已知，其它为变量）

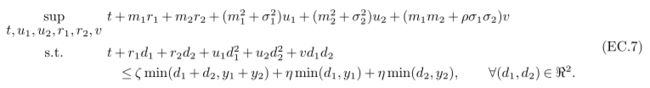
将每个 $\min$ 拆分下来，可以组装成6种情形：

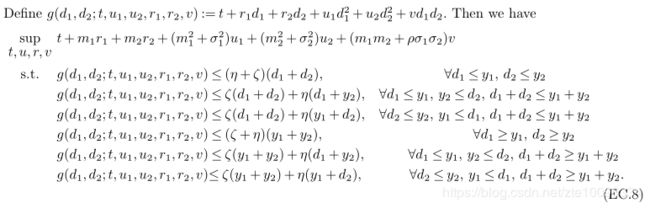
将函数 $g$ 记为 $g(d_1,d_2)$ (忽略对偶变量$t,u_1,u_2,r_1,r_2,v$)，它的上界是一个带有六个平面(six facets)的分段线性函数，假设$q_i(d_1,d_2)$代表每个平面的线性函数。

考虑这种情形： $g(d_1,d_2)$和分段线性函数正好相交于6个点，每个点都在各自一个平面上。如何计算这些点呢？

(1) 对每个 $i$，计算 $▽g(d_1,d_2)=▽q_i(d_1,d_2)$，求得 $(d_1^{\ast },d_2^{\ast })$，将它们表示为对偶变量$t,u_1,u_2,r_1,r_2,v$的一个函数；
(2) 令 $g(d_1^{\ast },d_2^{\ast })=q_i(d_1^{\ast },d_2^{\ast })$，它给出了两个函数刚好相交于一点的条件。

由此方法，可以得到

3. 参考文献

A. Govindarajan, A. Sinha, J. Uichanco. Distribution-free Inventory Risk Pooling in a Multi-location Newsvendor.