AtCoder Beginner Contest 174 C Repsept

Repsept

题目：

Takahashi loves the number 7 and multiples of K.Where is the first occurrence of a multiple of K in the sequence 7,77,777,…? (Also see Output and Sample Input/Output below.)
If the sequence contains no multiples of K, print -1 instead.

Input
Input is given from Standard Input in the following format:
K
Output
Print an integer representing the position of the first occurrence of a multiple of K, (For example, if the first occurrence is the fourth element of the sequence, print 4.)

输入样例1 (Sample Input 1)
101
输出样例1 (Sample Output 1)
4
输入样例2 (Sample Input 2)
2
输出样例2 (Sample Output 2)
-1
输入样例3 (Sample Input 3)
999982
输出样例3 (Sample Output 3)
999983

题目连接：

https://atcoder.jp/contests/abc174/tasks/abc174_c

题意分析：

给你一个整数K，再给你一个序列 7,77,777,…， 这个序列中，第一个是 K 的倍数的数是序列中的第几个？
如果该序列中不存在任何是 K 的倍数的数，请输出 -1。

算法分析：

本蒟蒻首先想到的是暴力的O(K)算法，看到大犇写的有O(K−−√logK)算法，等我学会了再补充 。
首先，我们不难发现这是一道推公式的初等数论题， 7,77,777,…这种超长字符串不好处理，我们先进行转换：

不难发现，左边是一个等比数列求和的形式。
于是，问题转化为了：
我们要找到一个最小的i使得

也就是

于是，我们开始化简：
设d=gcd(9K,7),
因为gcd(9,7)=1，
所以d=gcd(k,7);
我们将式子两边同时除以d，得到

左边的K/d和右边的7/d是互质的，所以可以把7/d直接删去。
所以式子变成了：

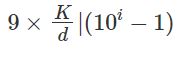
我们发现K/d是一个常数，则设c=9K/d。
最后式子变成了：

我们这时一拍大腿惊奇的发现这是欧拉函数！

在数论中，欧拉定理,（也称费马-欧拉定理）是一个关于同余的性质。欧拉定理表明，若n,a为正整数，且n,a互质，则:

φ(n)代表的含义是：小或等于n的正整数中与n互质的数的数目。
（因为10的公因数有1,2，5,10，而K想要有解必须尾数为1,3，7,9，所以10和c肯定是互质的）
于是φ©代表的是我们所要求的一个解，但并不是正确答案，因为所求的的i要求最小。
于是我们枚举1~φ©中所有的数。

时间复杂度证明：

因为枚举φ©还要多写一个函数，所以可以直接枚举到9K，φ© 这样的话复杂度就是O(K)。（可能这题数据有点水，我比赛的时候枚举K也过了。。。）

比赛时AC的代码

#pragma GCC optimize(2)
#include
using namespace std;
#define IOS ios::sync_with_stdio(0)
#define ull unsigned ll
#define uint unsigned
#define pai pair
#define pal pair
#define IT iterator
#define pb push_back
#define fi first
#define se second
#define For(i,j,k) for (int i=(int)(j);i<=(int)(k);++i)
#define Rep(i,j,k) for (int i=(int)(j);i>=(int)(k);--i)
#define endl '\n'
typedef long long ll;//头文件
int main()
{
    int k;
    cin>>k;
    int target=7%k;//枚举的数%K的结果
    int cnt=1;//统计枚举次数
    while(cnt<=k)
    {
        if(target==0)
        {
            cout<<cnt<<endl;
            return 0;
        }
        target=(target*10+7)%k;
        cnt++;
    }
    cout<<-1<<endl;
}

这是我写的第一篇博客，有很多地方还不会使用，如有侵权或者不足的地方，请联系我。