并查集-算法详解及例题(最小生成树问题)
一、并查集的概念:
并查集(Union-find Sets)是一种非常精巧而实用的数据结构,它主要用于处理一些不相交集合的合并问题。一些常见的用途有求连通子图、求最小生成树的 Kruskal 算法和求最近公共祖先(Least Common Ancestors, LCA)等。
使用并查集时,首先会存在一组不相交的动态集合 S={S1,S2,⋯,Sk}S={S1,S2,⋯,Sk},一般都会使用一个整数表示集合中的一个元素。每个集合可能包含一个或多个元素,并选出集合中的某个元素作为代表。每个集合中具体包含了哪些元素是不关心的,具体选择哪个元素作为代表一般也是不关心的。我们关心的是,对于给定的元素,可以很快的找到这个元素所在的集合(的代表),以及合并两个元素所在的集合,而且这些操作的时间复杂度都是常数级的。
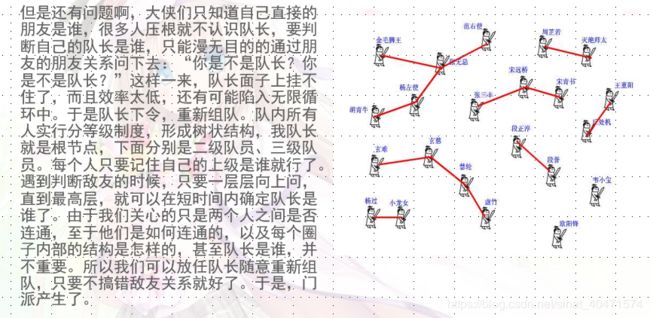
关于并查集的介绍,有一套非常生动形象的解说
二、例题分析:
结合一道例题简单对ppt中的代码进行一下补充。有些功能我没有写成函数,因为要实现的功能比较简单而且代码耦合度不高。
题目:畅通工程:http://acm.nefu.edu.cn/problemShow.php?problem_id=210
说一下思路:首先开一个数组a,表示每一条路的老大,我们让它的老大都是自己,即每一条路现在都不与其它路相连。每输入一组数据,我们分别找到它们的老大,如果它们的老大不一样,那么我们就让其中一个的老大变成另一个老大的小弟。最后就会形成一种树状结构,在树里的路都已连接,而不在树里的路就没有连接,按数组来说,就是a[i]不等于自己的说明被连接。那么遍历数组,计算a[i]=i的个数即得到答案。
看代码(不进行路径压缩):
#include
using namespace std;
int a[1005];
int main()
{
int n,m,i,num;
int city1,city2;
while(scanf("%d",&n)!=-1)
{
if(n==0) break;
scanf("%d",&m);
for(i=1;i<=n;i++) a[i]=i; //让每条路的老大都是自己
for(i=1;i<=m;i++)
{
scanf("%d %d",&city1,&city2);
while(a[city1]!=city1) //找第一条路的老大
city1=a[city1];
while(a[city2]!=city2) //找第二条路的老大
city2=a[city2];
if(city1!=city2) //此时的city1与city2已经分别是它们的老大,看它们是否相等,否则就让一个成为其中一个的小弟
a[city1]=city2;
}
num=-1; //因为连通的树的老大也等于自己
for(i=1;i<=n;i++)
if(a[i]==i) num++;
printf("%d\n",num);
}
} while部分就相当于ppt中的find()函数,if部分就相当于join()函数。
代码(路径压缩):
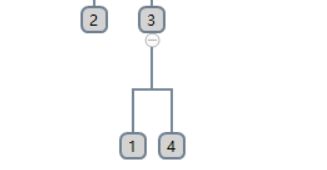
以题中样例一为例,最后生成的树状结构如图一,我们假设再生成如图2所示的路径,然后让2和3相连,就形成如图3的样子,发现这种写法是没有进行路径压缩的。
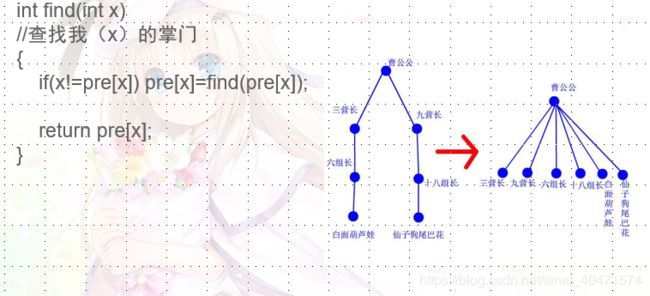
那么如何进行路径压缩呢?一种是如ppt中的递归写法,另一种是while循环写法。
先看while循环写法:直接让两棵树归到一棵上。
#include
using namespace std;
int main()
{
int a[1005];
int n,m;
int city1,city2,father,tmp1,tmp2;
while(scanf("%d",&n)!=-1)
{
if(n==0) break;
scanf("%d",&m);
for(int i=1;i<=n;i++) a[i]=i;
for(int i=1;i<=m;i++)
{
scanf("%d%d",&city1,&city2);
tmp1=city1;
while(a[city1]!=city1)
city1=a[city1];
father=city1; //也可以是city2
city1=tmp1;
while(a[city1]!=father)
{
int tmp=a[city1];
a[city1]=father;
city1=tmp;
}
while(a[city2]!=father)
{
int tmp=a[city2];
a[city2]=father;
city2=tmp;
}
}
int num=-1;
for(int i=1;i<=n;i++) if(a[i]==i) num++;
printf("%d\n",num);
}
}
递归写法:分别压缩两棵树,然后让一棵树接到另一棵树下。
#include
using namespace std;
int a[1005];
int findn(int x) //递归的神奇之处,找完以后可以倒回来改变
{
if(a[x]!=x) return a[x]=findn(a[x]);
return a[x];
}
void join(int x,int y)
{
int father1=findn(x);
int father2=findn(y);
if(father1!=father2) a[father1]=father2;
}
int main()
{
int n,m;
int city1,city2,father,tmp1,tmp2;
while(scanf("%d",&n)!=-1)
{
if(n==0) break;
scanf("%d",&m);
for(int i=1;i<=n;i++) a[i]=i;
for(int i=1;i<=m;i++)
{
scanf("%d%d",&city1,&city2);
join(city1,city2);
}
int num=-1;
for(int i=1;i<=n;i++) if(a[i]==i) num++;
printf("%d\n",num);
}
}
两种方法可以根据实际情况组合使用。
三、实战(最小生成树问题):
1. P3366 【模板】最小生成树:https://www.luogu.org/problemnew/show/P3366
最小生成树问题的概念和解题思路离散上已经讲过了,我就不重复了,我们直接看一下代码上如何利用并查集实现。
#include
using namespace std;
int a[5005];
struct node{ //节点,用于记录边和权值
int from;
int to;
int value;
}b[200005];
bool cmp(node x,node y) //按权值从小到大对b进行排序
{
return x.value>b[i].from>>b[i].to>>b[i].value;
}
sort(b,b+m,cmp); //按权值从小到大排序
ans=0;
cnt=0;
for(int i=0;i 2. P2820 局域网:https://www.luogu.org/problemnew/show/P2820
也是最小生成树问题,不过这回记的是多余边的权值,注意不能if(cnt==n-1)然后break,因为我们要遍历完所有边。
#include
using namespace std;
int a[105];
struct node{
int from;
int to;
int value;
}b[2000005];
bool cmp(node x,node y)
{
return x.value>b[i].from>>b[i].to>>b[i].value;
sort(b,b+k,cmp);
ans=0;
for(int i=0;i 3. P1195 口袋的天空:https://www.luogu.org/problemnew/show/P1195
这题题目说得不清不楚的,总的意思来说就是给你n个节点,怎么让这n个节点通过边的连接分成k个树(包括单个节点)。
要想连出k棵树,就需要连n-k条边,且不能有环和平行边。
#include
using namespace std;
int a[1005];
struct node{
int from;
int to;
int value;
}b[10005];
bool cmp(node x,node y)
{
return x.value>n>>m>>k;
for(int i=1;i<=n;i++) a[i]=i;
for(int i=0;i>b[i].from>>b[i].to>>b[i].value;
sort(b,b+m,cmp);
ans=cnt=0;
for(int i=0;i 4. P1547 Out of Hay:https://www.luogu.org/problemnew/show/P1547
模板题了,练练手。
#include
using namespace std;
int a[2005];
struct node{
int from;
int to;
int value;
}b[10005];
bool cmp(node x,node y)
{
return x.value>n>>m;
int maxn,cnt;
for(int i=1;i<=n;i++) a[i]=i;
for(int i=0;i>b[i].from>>b[i].to>>b[i].value;
sort(b,b+m,cmp);
maxn=-1;
cnt=0;
for(int i=0;i