Σ-Δ型模数转换器（ADC）
前言
越来越多的应用，例如过程控制、称重等，都需要高分辨率、高集成度的ADC。新型Σ-Δ转换技术恰好可以满足这些要求。Σ-Δ型模数转换器正以其分辨率高、线性度好、成本低等特点得到越来越广泛的应用。然而，很多设计者对于这种转换技术并不十分了解，因而更愿意选用传统的逐次比较ADC。Σ-Δ转换器中的模拟部分非常简单（类似于一个1bit ADC），而数字部分要复杂得多，按照功能可划分为数字滤波和抽取单元。由于更接近于一个数字器件，Σ-ΔADC的制造成本非常低廉。目前，Σ-Δ型模数转换器主要用于高分辨率的中、低频(低至直流)测量和数字音频电路。目前已经出现了高速Σ-Δ型模数转换器产品。例如AD7723(1.2MSPS)，AD9260(2.5MSPS)等。
工作原理
与一般的ADC不同，∑–△型ADC不是直接根据抽样数据的每一个样值的大小进行量化编码，而是根据前一量值与后一量值的差值即所谓的增量的大小来进行 量化编码。从某种意义上讲，它是根据信号波形的包络线进行量化编码的。∑–△型ADC由两部分组成，第一部分为模拟∑–△调制器，第二部分为数字抽取滤波器，如下图所示。 
∑–△调制器以极高的抽样频率对输入模拟信号进行抽样，并对两个抽样之间的差值进行低位量化，从而得到用低位数码表示的数字信号即∑–△码；然后将这种∑–△码送给第二部分的数字抽取滤波器进行抽取滤波，从而得到高分辨率的线性脉冲编码调制的数字信号。因此抽取滤波器实际上相当于一个码型变换器。由于∑–△调制器具有极高的抽样速率， 通常比奈奎斯特抽样频率高出许多倍，因此∑–△调制器又称为过抽样ADC转换器。
这种类型的ADC采用了极低位的量化器， 从而避免了制造高位转换器和高精度电阻网络的困难；另一方面，因为它采用了∑–△调制技术和数字抽取滤波，可以获得极高的分辨率；同时由于采用了低位量化输出的∑–△码，不会对抽样值幅度变化敏感，而且由于码位低，抽样与量化编码可以同时完成，几乎不花时间，因此不需要采样保持电路，这就使得采样系统的构成大为简化。这种增量调制型ADC实际上是以高速抽样率来换取高位量化，即以速度来换精度。
从调制编码理论的角度看，多数传统的ADC，例如并行比较，逐次逼近型等，均属于线性脉冲编码调制(LPCM，Linear Pulse Code Modulation)类型。这类ADC根据信号的幅度大小进行量化编码，一个分辨率位n的ADC其满刻度电平被分为2n个不同的量化等级，为了能区分这2n个不同的量化等级需要相当复杂的电阻(或电容)网络和高精度的模拟电子器件。当位数n较高时，比较网络的实现是比较困难的，因而限制了转换器分辨率的提高。同时，由于高精度的模似电子器件受集成度，温度变比等因素的影响，进一步限制了转换器分辨率的提高。
∑–△型ADC与传统的LPCM型ADC不同，它不是直接根据信号的幅度进行量化编码，而是根据前一采样值与后一采样值之差(即所谓增量)进量化编码，从某种意义上来说它是根据信号的包络形状进行量化编码的。从这一点上看，它与跟踪计数型ADC有一点类似。
△表示增量，∑表示积分或求和。在下面可以看到，∑–△型ADC采用了极低位的量化器(通常是1位)，从而避免了LPCM型ADC在制造时面临的很多困难，非常适合用MOS技术实现。另一方面，又因为它采用了极高的采样速率和∑–△调制技术，可以获得极高的分辨率。同时，由于它采用低位量化，不会像LPCM型ADC那样对输入信号的幅度变化过于敏感。
与传统LPCM型ADC相比，∑–△型ADC实际上是一种用高采样速率来换取高位量化，即以速率换分辨率的方案。
过采样技术
是改善模数转换器总体性能诸多技术中的一种。∑—△结构的ADC是一种内在的过采样转换器。∑—△型ADC以很低的采样分辨率(1位)和很高的采样速率将模拟信号数字化，通过使用过采样技术，噪声整形和数字滤波技术增加有效分辨率，然后对ADC输出进行抽取(Decimation)处理，以降低ADC的有效采样速率，去除多余信息，减轻数据处理的负担。由于∑—△型ADC所使用的1位量化器(即1位比较器)和1位数模转换器(为一开关)具有良好的线性，所以∑—△型ADC表现出的微分线性和积分线性性能是非常优秀的，并且，不像其它类型的ADC那样，它无需任何的修调。
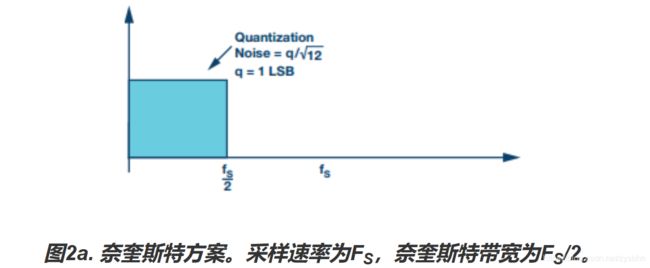
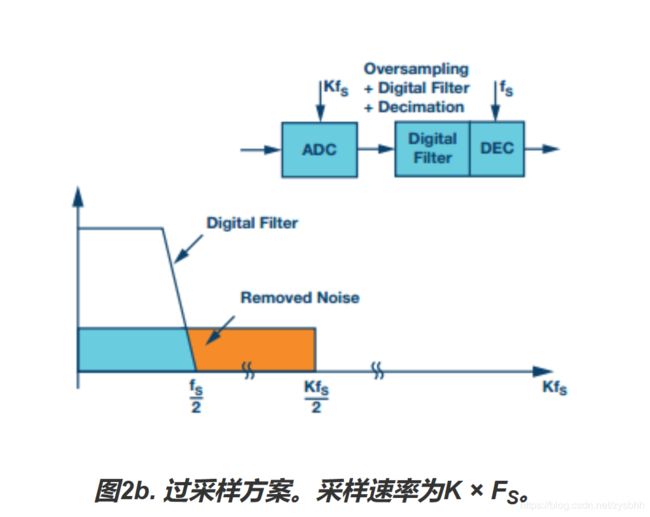
图2a显示了ADC以标准奈奎斯特方式运行时的量化噪声。这种情况下，量化噪声由ADC的LSB大小决定。FS为ADC的采样速率，FS/2为奈奎斯特频率。图2b显示的是同一转换器，不过现在它以过采样方式运行，采样速率更快。采样速率提高K倍，量化噪声扩展到K × FS/2的带宽上（好像是因为采样数目多，噪声平均功率降低了）。低通数字滤波器(通常带抽取功能)可消除蓝色区域之外的量化噪声。
Σ-Δ调制器多了一个特性，那就是噪声整形，如图2c所示。模数转换的量化噪声被调制整形，从低频移动到较高频率(通常如此)，低通数字滤波器可将其从转换结果中消除。Σ-Δ型ADC的噪底由热噪声决定，而不受量化噪声的限制。
采样、调制、滤波
Σ-Δ型ADC使用内部或外部采样时钟。ADC的主时钟(MCLK)常常要先分频，再交由调制器使用；阅读ADC数据手册时应注意这点，并了解调制器频率。传送到调制器的时钟设置采样频率FMOD。调制器以该速率将数据输出到数字滤波器，进而数字滤波器(通常为低通，带抽取功能)以输出数据速率(ODR)提供数据。图3显示了这一过程。
一阶∑–△型ADC的基本原理
Σ-Δ调制器是一种负反馈系统，与闭环放大器相似。环路包含低分辨率ADC和DAC，以及一个环路滤波器。输出和反馈被粗略量化，常常只有一比特表示高电平或低电平的输出。ADC的模拟系统实现了这种基本结构，量化器就是完成采样的模块。如果存在保证环路稳定的条件，那么输出就是输入的粗略表示。数字滤波器获得该粗略输出并重构模拟输入的精确数字转换结果。
图4显示了响应一个正弦波输入的1密度输出。调制器输出从低电平到高电平的变化率取决于输入的变化率。当正弦波输入为正满量程时，调制器输出开关速率会降低，输出以+1状态为主。同样，当正弦波输入为负满量程时，+1和–1之间的转换会减少，输出以–1为主。当正弦波输入处于最大变化率时，调制器输出发生最高密度的+1和–1切换。（输入信号的斜率越大+1、-1之间的切块越快，联想一下积分的过程）输出变化率与输入变化率同步。因此，模拟输入由Σ-Δ调制器输出的转换率来描述。
若使用线性模型来描述这种1位调制器(Mod 1)，则可将该系统表示为一个带负反馈（Δ）的控制系统。量化噪声为量化器的输入与输出之差。输入偏差节点之后是一个低通滤波器。在图5b中，量化噪声用N来表示。
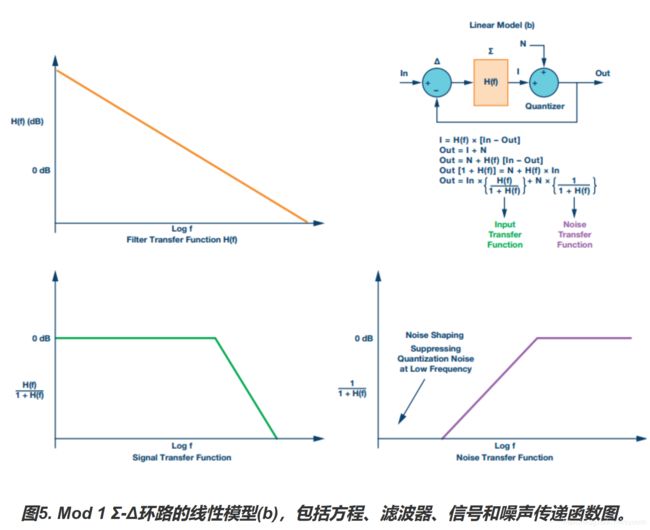H(f)是环路滤波器的函数，定义噪声和信号的传递函数。H(f)是一个低通滤波器函数，在低频(目标带宽内)时具有非常高的增益，可衰减高频信号。环路滤波器可实现为简单的积分器或积分器级联。实践中常常把一个DAC放在反馈路径中，以便获取数字输出信号并将其转换为模拟信号反馈到模拟输入偏差节点。
解出图5所示方程便可得到信号和噪声传递函数。信号传递函数用作一个低通滤波器，在目标带宽内的增益为1。噪声传递函数是一个高通滤波器函数，提供噪声整形，在DC附近的较低频率，对量化噪声有很强的抑制。在超出目标带宽的较高频率看到的量化噪声会增加。对于一阶调制器(Mod 1)，噪声以大约20 dB/十倍频程的速率提高。
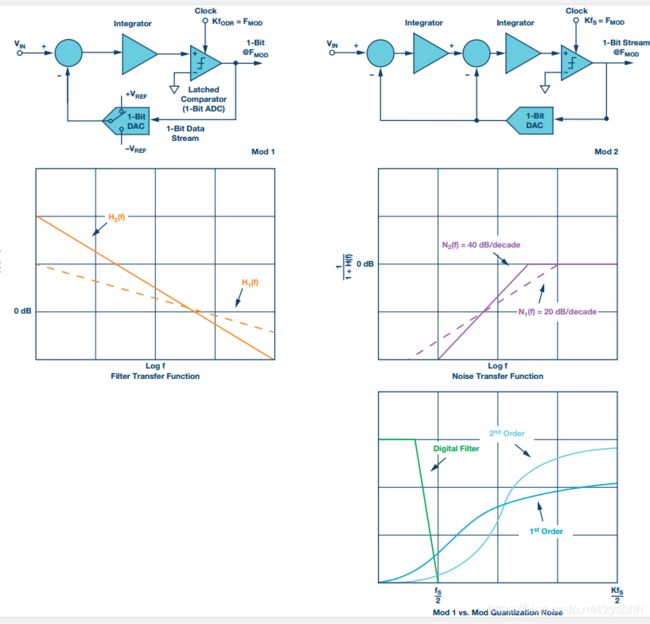
为了提高系统分辨率，常见方法是将两个环路滤波器级联起来以增加环路滤波器阶数。现在，总环路滤波器的H(f)具有更大的滚降，Mod 2型的噪声传递函数具有40 dB/十倍频程的上升速率。噪声所处的频率越低，噪声整形就越厉害。图6比较了Mod 1型和Mod 2型Σ-Δ ADC。Σ-Δ调制器的变化和样式非常多。 规避了高阶1位环路稳定性问题的架构称为多级噪声整形调制器(MASH)架构。多级(MASH型)架构支持通过具有内在稳定性的低阶环路组合来设计稳定的高阶Σ-Δ调制器。
消除Σ-Δ ADC量化噪声：噪声和带宽考虑因素
图4显示了调制器原始噪声来源与AD7175器件从DC到FMOD/2 (或4 MHz)的频率对数的关系。AD7175调制器以8 MHz (FMOD)的有效速率采样。调制器为MASH型，对调制器噪声提供80 dB/十倍频程的衰减速率。电路的热噪声决定了调制器噪声开始以斜坡变化之前频带内的噪底。从显示低噪底的曲线可以看出该ADC对低 带宽信号的高动态范围能力。此动态范围以及AD7175降低噪底的能力可用来改善应用的灵敏度，这在采集低幅度信号时特别有用。
ADC的最低过采样比、数字滤波器阶数和转折频率都有助于确保量化噪声不是ADC噪声的限制因素。为了滤除噪声，滤波器的包络必须能够以足够大的滚降速率进行衰减，从而应对幅度量化噪声的增速。
AD7175的最低过采样比为×32，在8 MHz FMOD条件下，最大输出数据速率为250 kHz。
AD7175提供了多种不同类型的滤波器，可供用户选择。数字滤波器的工作原理是通过比较不同情况下的sinc5 + sinc1和sinc3滤波器来说明的。
在250 kHz ODR时，AD7175 sinc5 + sinc1可直接配置为sinc5，其−3 dB频率为~0.2 × ODR (50 kHz)。sinc5滤波器的衰减包络为−100 dB/十倍频程。这意味着sinc5滤波器的衰减和滚降速率足以消除调制器噪声，如图3所示。
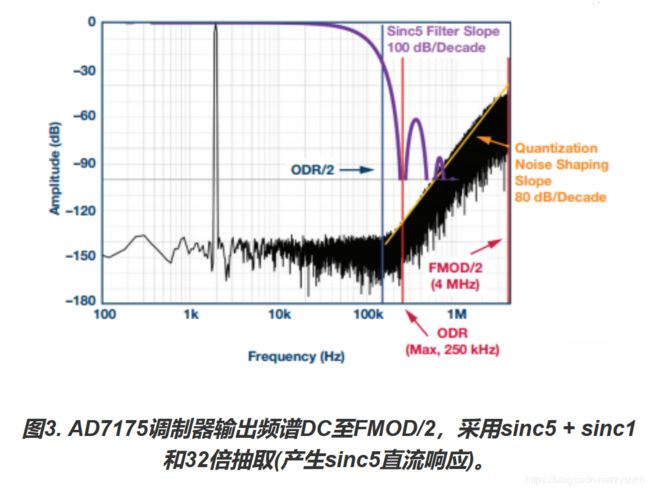
相比之下，若更改为250 kHz ODR的sinc3，衰减和滚降速率将不足以消除调制器噪声。数据手册中的250 kHz和125 kHz ODR时的噪声数值说明了这一情况。只有将数据速率设置为62.5 kHz或更低，sinc3响应才能完全滤除ADC结果中的量化噪声。
除了滤除量化噪声以外，数字滤波器还能通过调整输入带宽来降低噪声。这是通过提高抽取率实现的。对于sinc5 + sinc1滤波器，提高过采样比意味着初始五阶sinc滤波器要进行均值计算。利用初始结果的均值，用户可以选择不同的输出数据速率、速度和带宽来改善噪声性能(如图5所示)，即先由sinc5再由sinc5 + sinc1求均值来改善噪声性能。对sinc5结果求均值会引入频率为输出数据速率及其倍数的一阶陷波，这些陷波会与sinc5总包络复合。sinc型滤波器中的陷波频率传统上是用来抑制已知频率的干扰信号，即通过把数据速率策略性地设置为与干扰频率重合。一个经典例子是50 Hz和60 Hz的工频抑制。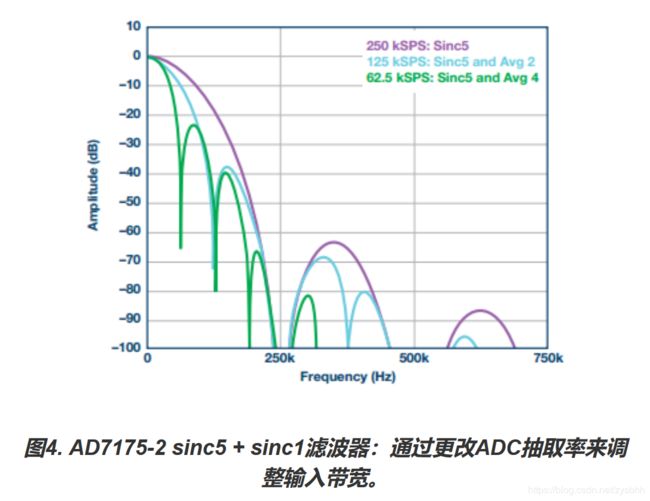
sinc型滤波器是具有sin(x)/x剖面的移动平均滤波器，因此一般称其为sinc滤波器。该滤波器由一系列积分器、一个用作抽取率的开关和一系列微分器组成。它是一种有限脉冲响应(FIR)型滤波器。对于输入的阶跃变化，它表现出已知且有限的线性相位响应。深陷波发生在输出数据速率及其整数倍处，陷波内的信号会被衰减。
图6比较了AD7175的三阶和五阶sinc滤波器，二者均以32倍抽取率运行。这种情况下，两个滤波器均以250 kHz的输出速率提供转换数据。滤波器的阶数决定滚降速率和−3 dB频率。sincP滤波器位于–P × 20 dB/十倍频程的频率响应包络之下。滚降越陡，−3 dB频率越低。不同阶数滤波器之间的主要区别在于滤波器建立时 间，根据情况不同，其对终端测量应用的影响也不同。
滤波器建立时间
当数字滤波器处理来自Σ-Δ调制器的数据流的移动平均值时，存在一个相关的建立时间。该延迟对所有FIR滤波器是固定的，**但对不同阶数的sinc滤波器，该延迟是不同的。通常用两项来描述该延迟：群延迟和建立时间。群延迟描述从输入端存在模拟信号到在数字输出端看到它的延迟时间。**例如，对于单音正弦 波，群延迟就是从模拟输入端存在该正弦波电压峰值到该峰值出现在数字输出端的时间差。
**建立时间是指数字滤波器的全部均值时间。如果模拟输入端有一个阶跃，那么需要经过滤波器的完全建立时间，ADC的数据输出才与阶跃之前的输入无关。**还可能存在其他延迟，如滤波器的计算时间等。对于AD7175系列，第一次转换会有较长的建立时间；由于初始计算周期为1/ODR，离开待机状态后的建立也可 能引起延迟。除滤波器建立时间之外的延迟可能依选择的转换器不同而异，因此，阅读ADC数据手册时应留心。
通过比较单一Σ-Δ ADC与多路复用Σ-Δ ADC，可以更好地说明滤波器建立时间影响。数字滤波器的建立时间会严重影响多个输入通道循环转换的速率，因为要保持各通道的结果独立。
为什么要等待完全建立时间之后才能给出独立结果？让我们看看采用单一输入源的单通道ADC的数字滤波。来自Σ-Δ ADC调制器的数据以FMOD的速率传送到数字滤波器(如图5所示)，每个样本都通过移动平均滤波器。根据阶数和类型不同，滤波器在转换期间(由滤波器抽取率设置)内以不同方式衡量各样本，如图 7所示。输入样本0和随后的样本是调制器在其每个时钟周期的离散输出结果。y轴表示数字滤波器衡量各样本而给出的权重比例。此权重的形状就是低通数字滤波器的时域表示。这种情况下的输出数据速率为250 kHz (8 MHz/32 = FMOD/抽取率)。数据就绪信号(各种颜色的竖直虚线)之间的时间为4 μs。ADC采用sinc5 + sinc1滤波器和32倍抽取率运行。在定义滤波器输出为调制器的模拟输入时，所有五个转换输出都有一定的重叠，因此，没有输出是各自独立的。对于单一ADC输入，各转换结果共享调制器模拟输入，但滤波器以不同权重衡量各调制器输出。
**对于多路复用输入情况，调制器产生的每个转换数据对各通道必须是独立的。必须经过滤波器的完全建立时间之后，多路复用器才能从一个模拟输入通道切换到另一个模拟输入通道。**以sinc3型滤波器为例，使用32倍抽取率，一次转换的滤波器建立时间如图8(a)所示。一旦滤波器完全建立，数据输出便是先前96 个调制器输出的加权平均值。这相当于12 μs或三个周期的ADC输出数据速率。
图8(b)显示了多路复用情况的前三个样本，ADC输出的各样本均已完全建立。在任何样本之间，调制器输出都没有重叠。DRDY(竖直线)之间的时间所指示的复用速率由滤波器的建立时间决定。此速率在数据手册和性能曲线中常常是作为完全建立数据速率来描述。
对于sincP滤波器，滤波器的建立时间为滤波器阶数P乘以1/ODR。对于以250 kHz ODR运行的sinc3滤波器，其建立时间为3 ×1/250 kHz = 12 μs。作为比较，若使用sinc5滤波器，ODR同为250 kHz，则建立时间为5 × (1/2 50 kHz) = 20 μs。
近似的通道切换速率为ODR除以滤波器阶数，也就是ODR/3 (对于sinc3滤波器)或ODR/5 (对于sinc5滤波器)。对于直接sinc滤波器，这是很显然的。对于sinc5 + sinc1型滤波器，需要增加一个步骤。AD7175系列ADC允许选择不同类型的滤波器。下一部分将介绍不同类型滤波器之间的区别，并提供一个例子来说明如何 计算各种情况下的建立时间。
现在看看多路复用情况下的建立时间。在过程控制和工厂自动化中，典型的模拟输入模块会有一个前端调理，用以将±10 V输入调整到AD7175-8的输入范围内。然后，AD7175-8会复用各通道，按顺序转换各输入或输入对。完成所有通道转换的时间取决于所用的滤波器和通道数目。
下例对使用sinc3滤波器和使用sinc5 + sinc1滤波器进行了比较，二者配置为相同的输出数据速率，我们会看到建立时间计算的对比和方法。用户可以选择AD7175-8的这两个滤波器选项。
a. 使用sinc3滤波器，62.5 kHz ODR 计算建立时间。
AD7175 sinc3: ODR = 62.5 kHzz
建立时间 = 3 × (1/62.5 kHz) = 48 μs。
通道开关速率 = 1/48 μs = 20.833 kHz
b. 使用sinc5 + sinc1滤波器，62.5 kHz ODR 计算建立时间。
AD7175 sinc5 + sinc1: ODR = 62.5 kHz
注意有两个部分。sinc5滤波器在4 μs窗口上求均值(FMOD = 8 MHz)，因此它以250 kHz的速率将数据传送到均值模块。
-
sinc5的建立时间 = 5 × 1/250 kHz = 20 μs。
这提供均值计算的第一个样本。 -
sinc1的建立，均值滤波器。
对于ODR = 62.5 kHz，250 kHz数据流四次求均值。
用于均值计算的剩余三个样本的建立
时间为3 × 1/250 kHz = 12 μs。
总建立时间 = 20 μs + 12 μs = 32 μs，
通道开关速率 = 1/32 μs = 31.25 kHz。
注意：对于sinc5 + sinc1滤波器，当数据速率为10 kSPS及以下时，ADC具有单周期建立特性。这意味着ADC的建立时间为1/ODR。
表2显示了采用设置(a)和(b)的4通道多路复用测量的比较。使用sinc5 + sinc1滤波器可提高每通道采样速率，说明较短建立时间有优势。注意：这个经验法则仅适用于转换器，若各路输入之前有模拟预调理电路，并且其时间常数比ADC要长，那么起主导作用的将是最差情况建立时间。
一阶∑—△型ADC
含有非常简单的模拟电路和十分复杂的数字信号处理电路：
Σ-Δ转换器具有相对简单的结构，又称为过采样转换器。这种转换器由Σ-Δ调制器（虚线框内）及连接于其后的数字滤波器构成。调制器的结构非常近似于双斜率ADC，包括一个积分器和一个比较器，以及含有一个1位ADC的反馈环。这个内置的DAC仅仅是一个开关，它将积分器输入切换到一个正或负的参考电压。Σ-ΔADC还包括一个时钟单元，为调制器和数字滤波器提供适当的定时。
下图是输入Vin＝0和Vin＝＋Vref/4两种情况下，电路中各点的电压波形示意图。可以看出两种情况下，C点输出的码流中"0"和"1"的个数是不一样的。
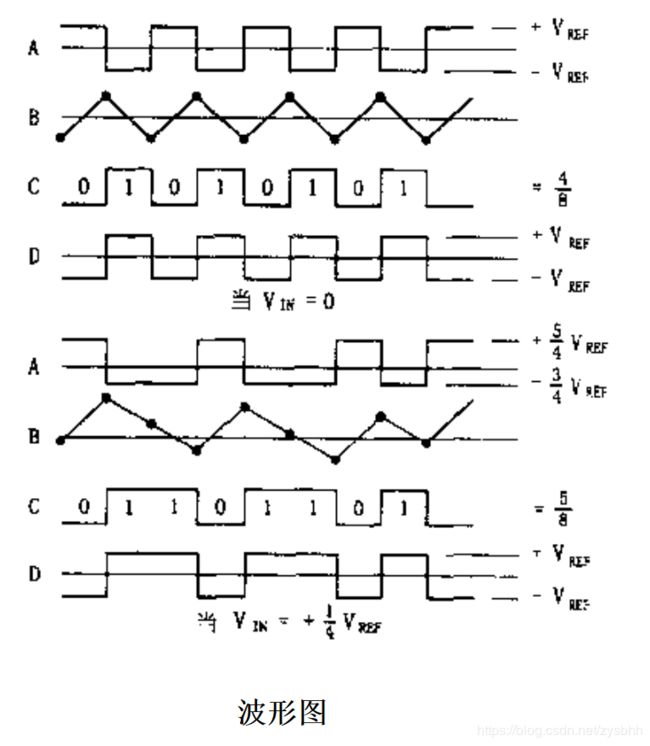窄带信号送入Σ-ΔADC后被以非常低的分辨率（1位）进行量化，但采样频率却非常高，如2MHz或更高。经过数字滤波处理后，这种过采样被降低到一个比较低的采样率，如8KHz左右，同时ADC的分辨率（即动态范围）被提高到16位或更高，尽管比流水线ADC要慢且限于比较低的输入带宽，这种Σ-Δ技术在模数转换器市场上仍占据了很重要的位置。它具有三个主要优势：
低价格、高性能(最高可到24位)
集成化的数字滤波
与DSP技术的兼容性便于实现系统集成
主要应用在：音频和测量
发展状况
近年来，采用高分辨率的Σ-Δ型ADC颇为流行，它的一个突出优点是在一片混合信号CMOS大规模集成电路上实现了ADC与数字信号处理技术的结合。这一技术的其它优点：分辨率高达24位；比积分型及压频变换型ADC的转换速率高； 采用混合信号CMOS工艺，可实现低价格、高分辨率的数据采集和数字信号处理；由于采用高倍频过采样技术，降低了对传感器信号进行滤波的要求，实际上取消了信号调理。缺点：当高速转换时，需要高阶调制器；在转换速率相同的条件下，比积分型和逐次逼近型ADC的功耗高。
目前，Σ-Δ型ADC分为四类：（1）高速类ADC；（2）调制解调器类ADC；（3）编码器类ADC；（4）传感器低频测量ADC。其中每一类Σ-Δ型ADC又分为许多型号，给用户带来极大方便。
总结
通常包括两个模块：Σ-Δ调制器和数字信号处理模块，后者通常是数字滤波器。Σ-Δ调制器是一种过采样架构。因为想通过超高的采样速度从而通过Δ能将包络描述出来，又由于Σ-Δ调制器阶段高频率会产生较高的量化噪声（量化噪声是高通），因此再设计一个数字滤波器进行滤波。