基于匹配点集对单应性矩阵进行估计

基于匹配点集对单应性矩阵进行估计

2020/4/28 FesianXu

前言

在立体视觉中，对单应性矩阵进行估计是一个很重要的任务，我们在之前的博文[1,2,3]中的讨论中都或多或少地涉及到了单应性矩阵，我们知道它是在投影变换中保持共线性的一种性质。在本文中，我们将讨论如何通过匹配点的关系，对单应性矩阵进行估计。如有谬误，请联系指出，转载请联系作者并注明出处，谢谢。

注：本文参考[7]的内容。

$\nabla$ 联系方式：
e-mail: [email protected]
QQ: 973926198
github: https://github.com/FesianXu

---

估计问题

估计（estimation）是什么？这个词我们在统计学中经常听到，估计指的是基于观测数据的基础上，对一个模型的参数进行估计，在立体视觉中，一般有以下几种估计问题：

1. 2D 单应性(2D homography)： 给定一系列点${\mathbf{x}}_i\in {\mathbb{P}}^2$，并且给定其对应的匹配点${\mathbf{x}}_i^{\prime }\in {\mathbb{P}}^2$，我们的估计的目标是根据这些对应点，估计出能够将$f:{\mathbf{x}}_i\to {\mathbf{x}}_i^{\prime }$的投影变换。在实际中，${\mathbf{x}}_i$和${\mathbf{x}}_i^{\prime }$通常是两张不同的图片上的对应/匹配点(match points)，每个图片都可以看成是投影空间${\mathbb{P}}^2$。在本路问题中，其实就是根据2D匹配点进行单应性矩阵$H\in {\mathbb{R}}^{3\times 3}$的估计。
2. 3D到2D的相机投影(3D to 2D camera projection)：给定在三维空间中的点${\mathbf{X}}_i$，并且给定这些3D点在平面图像上的对应的2D点${\mathbf{x}}_i$。在这里的估计指的就是估计这里的3D到2D的投影变换$f:{\mathbf{X}}_i\to {\mathbf{x}}_i$，这里的投影通常是由投影相机模型得到的，参考[4]的讨论内容。
3. 基础矩阵的计算(Fundamental matrix computation)：给定在一张图像上的一系列点${\mathbf{x}}_i$和其在另一张图像上的对应点集${\mathbf{x}}_i^{\prime }$，计算根据这些对应关系计算出来的基础矩阵，我们在[5]中介绍过本征矩阵和基础矩阵，我们知道基础矩阵$\mathcal{F}$是一个对所有的$i$都满足${{\mathbf{x}}_i^{\prime }}^{\mathrm{T}}\mathcal{F}{\mathbf{x}}_i=0$的$3\times 3$的矩阵。
4. 三焦张量计算(Trifocal tensor computation)： 给定三张图片中的对应关系：${\mathbf{x}}_i\leftrightarrow {\mathbf{x}}_i^{\prime }\leftrightarrow {\mathbf{x}}_i^{\prime \prime }$ ，计算其三焦张量(Trifocal tensor)， 三焦张量对三张图像的对应点或者对应线进行了关系联系。

这些问题都是考虑到了“对应性”（correspondance），或者说是“匹配性”，然后对某种变换进行参数估计，因此这四个问题或多或少有着关联。在此，我们仅讨论第一种问题，其中提出的解法，能对其他三种问题的解决提供思路。

估计单应性矩阵

重申下问题：

我们考虑两个图像之间的匹配点集${\mathbf{x}}_i\leftrightarrow {\mathbf{x}}_i^{\prime }$，我们需要估计出单应性矩阵$H$，使得对于所有的 $i$都有${\mathbf{x}}_i^{\prime }=H{\mathbf{x}}_i$。

首先我们需要确定至少需要多少对匹配点集才足以确定一个单应性矩阵，我们知道单应性矩阵有9个元素，但是其可以进行尺度归一化[6]，因此2D的单应性矩阵只有8个自由度（同理，3D的单应性矩阵为15的自由度）。每一对匹配点集提供了两个自由度的约束（也就是x和y），因此最少需要四对匹配点集才足以确定一个单应性矩阵。

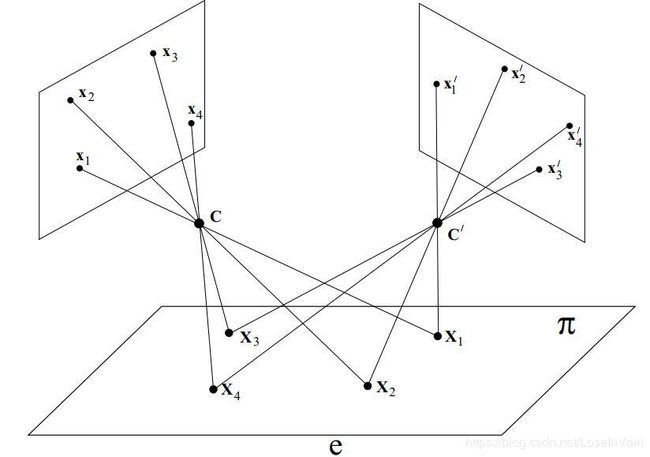
自然地，给定了4对匹配点集（其中不能是三点共线的，我们后续讨论），我们可以确定一个单应性矩阵，这个是最小解。然而在实际中，我们通常能得到两张图片的很多对匹配点集，如Fig 1.1所示，而通常在这很多的匹配点集中，存在有误匹配的情况，这些误匹配称之为噪声（noise），通常我们会采用类似于RANSAC的鲁棒估计减少噪声的干扰（我们将在以后的博文中讨论RANSAC鲁棒估计）。除了鲁棒估计，我们也可以通过设置一个损失函数（cost function），尝试最小化损失函数，我们能找到一个最佳的单应性矩阵估计。一般来说，有两大类的损失函数：

1. 基于代数损失的（algebraic error），也就是不考虑图像的几何上的因素，只考虑代数形式上的损失。
2. 基于几何损失（geometric error）或统计上的图像距离的（statistical image distance），这种损失函数通常带有图像几何上的意义。

Fig 1.1 在实际中，通常会有很多对的匹配点集，其中会存在有误匹配的点对，称之为噪声，可以通过例如RANSAC的鲁棒估计以减少噪声干扰。

通常在对同一个平面上的点进行多视角摄像时，如Fig 1.2，图像中的像素点可以视为是投影变换的，可以用单应性矩阵对应，在进行弱透视摄像时[9]，同样也可以这样认为。

Fig 1.2 在对现实中平面的物体进行成像时（或者弱透视情况下），可以视为是投影变换，用单应性矩阵进行对应。

DLT算法

我们首先考虑一个简单的线性算法。在给定了4对2D到2D的匹配点集时${\mathbf{x}}_i\leftrightarrow {\mathbf{x}}_i^{\prime }$，我们有${\mathbf{x}}_i^{\prime }=H{\mathbf{x}}_i$ （我们在齐次坐标系下进行处理[8]）。因为我们在齐次坐标系下，因此严格上说${\mathbf{x}}_i^{\prime }$和$H{\mathbf{x}}_i$在尺度（scale）上并不相同，而是有着同样的方向。因此为了更加精确，我们可以把这个线性关系表示为：
$${\mathbf{x}}_i^{\prime }\times H{\mathbf{x}}_i=0\text{\hspace{1em}(1.1)}$$
如果我们$H$的第$j$行表示为${{\mathbf{h}}^j}^{\mathrm{T}}$，那么我们有：
$$H{\mathbf{x}}_i=\left(\begin{array}{c}{{\mathbf{h}}^1}^{\mathrm{T}}{\mathbf{x}}_i\\ {{\mathbf{h}}^2}^{\mathrm{T}}{\mathbf{x}}_i\\ {{\mathbf{h}}^3}^{\mathrm{T}}{\mathbf{x}}_i\end{array}\right)\text{\hspace{1em}(1.2)}$$
将${\mathbf{x}}_i^{\prime }=(x_i^{\prime },y_i^{\prime },w_i^{\prime }{)}^{\mathrm{T}}$，那么式子(1.1)可以写成：
$${\mathbf{x}}_i^{\prime }\times H{\mathbf{x}}_i=\left(\begin{array}{c}{y}_i^{\prime }{{\mathbf{h}}^3}^{\mathrm{T}}{\mathbf{x}}_i-w_i^{\prime }{{\mathbf{h}}^2}^{\mathrm{T}}{\mathbf{x}}_i\\ w_i^{\prime }{{\mathbf{h}}^1}^{\mathrm{T}}{\mathbf{x}}_i-x_i^{\prime }{{\mathbf{h}}^3}^{\mathrm{T}}{\mathbf{x}}_i\\ x_i^{\prime }{{\mathbf{h}}^2}^{\mathrm{T}}{\mathbf{x}}_i-y_i^{\prime }{{\mathbf{h}}^1}^{\mathrm{T}}{\mathbf{x}}_i\end{array}\right)=0\text{\hspace{1em}(1.3)}$$
又因为有${{\mathbf{h}}^j}^{\mathrm{T}}{\mathbf{x}}_i={\mathbf{x}}_i^{\mathrm{T}}{\mathbf{h}}^j,j=1,\cdots ,3$，所以(1.3)可以写成：
$$\left[\begin{array}{ccc}{0}^{\mathrm{T}}& -w_i^{\prime }{\mathbf{x}}_i^{\mathrm{T}}& y_i^{\prime }{\mathbf{x}}_i^{\mathrm{T}}\\ w_i^{\prime }{\mathbf{x}}_i^{\mathrm{T}}& 0^{\mathrm{T}}& x_i^{\prime }{\mathbf{x}}_i^{\mathrm{T}}\\ y_i^{\prime }{\mathbf{x}}_i^{\mathrm{T}}& x_i^{\prime }{\mathbf{x}}_i^{\mathrm{T}}& 0^{\mathrm{T}}\end{array}\right]\left(\begin{array}{c}{\mathbf{h}}^1\\ {\mathbf{h}}^2\\ {\mathbf{h}}^3\end{array}\right)={\mathbf{A}}_i\mathbf{h}=0,{\mathbf{A}}_i\in {\mathbf{R}}^{3\times 9}\text{\hspace{1em}(1.4)}$$
我们发现，对于未知量$\mathbf{h}$而言，其是线性的，而且我们也可以发现这里的${\mathbf{A}}_i$的秩为2，只有两个方程式是线性无关的，将${\mathbf{A}}_i$的第$j$行表示为${\mathbf{A}}_i^j$，我们有：
$${\mathbf{A}}_i^3=x_i^{\prime }{\mathbf{A}}_i^1+y_i^{\prime }{\mathbf{A}}_i^2\text{\hspace{1em}(1.5)}$$
因此，我们可以将(1.4)去掉最后一行，得到
$$\left[\begin{array}{ccc}{0}^{\mathrm{T}}& -w_i^{\prime }{\mathbf{x}}_i^{\mathrm{T}}& y_i^{\prime }{\mathbf{x}}_i^{\mathrm{T}}\\ w_i^{\prime }{\mathbf{x}}_i^{\mathrm{T}}& 0^{\mathrm{T}}& x_i^{\prime }{\mathbf{x}}_i^{\mathrm{T}}\end{array}\right]\left(\begin{array}{c}{\mathbf{h}}^1\\ {\mathbf{h}}^2\\ {\mathbf{h}}^3\end{array}\right)={\mathbf{A}}_i\mathbf{h}=0\text{\hspace{1em}(1.6)}$$
此时的${\mathbf{A}}_i\in {\mathbb{R}}^{2\times 9}$

又因为这个表示是在齐次坐标系下的，我们可以让$w_i^{\prime }=1$。每一对匹配点都存在着一个如同(1.6)的等式约束，约束了两个自由度，因此在4对匹配点的情况下，我们的$\mathbf{A}\in {\mathbb{R}}^{8\times 9}$，当$\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}(\mathbf{A})=8$的时候，就存在非零解（平凡解）的$\mathbf{h}$，这点我们在线性代数中已经学习过了，求出了$\mathbf{h}$我们自然就知道了$H$。特别的，我们的$H$是和尺度有关的，任何尺度的$H$都满足(1.1)的条件（除了0之外），因此我们通常对其进行一个限制，比如对范数进行归一化，如$||\mathbf{h}||=1$。

当给出超过4对匹配点的时候，我们处在超定方程（over-determined）的情况，此时可能没有一个解可以精确地满足所有点的匹配关系，因此我们设计一个损失函数，让损失函数最小以达到最佳的估计效果。因为我们知道$\mathbf{A}\mathbf{h}=0$是整个匹配点集的最优解，因此我们尝试最小化这个函数:
$$\arg \underset{\mathbf{h}}{\min }||\mathbf{A}\mathbf{h}||\text{\hspace{1em}(1.7)}$$
然而，我们还有个约束:$||\mathbf{h}||=1$，因此整个问题等价于我们最小化：
$$\arg \underset{\mathbf{h}}{\min }=\frac{||\mathbf{A}\mathbf{h}||}{||\mathbf{h}||}\text{\hspace{1em}(1.8)}$$
(1.8)存在有解析解，其解是${\mathbf{A}}^{\mathrm{T}}\mathbf{A}$的最小的特征值所对应的单位特征向量，等价来说是$\mathbf{A}$的奇异值分解中最小奇异值对应的奇异向量，首先我们对给定的$\mathbf{A}$进行奇异值分解，有$\mathbf{A}=\mathbf{U}\mathbf{D}{\mathbf{V}}^{\mathrm{T}}$，我们知道其中的$\mathbf{D}$是一个对角矩阵，每个对角元都是一个奇异值，我们对这些奇异值进行降序排序，根据此更新特征向量${\mathbf{V}}^{\mathrm{T}}$的值排序，那么更新后的${\mathbf{V}}^{\mathrm{T}}$最后一列就是最小的奇异值对应的奇异向量，也就是我们要的解 $\mathbf{h}$。这个算法被称之为DLT，Direct Linear Transformation算法。

其他的损失函数

代数距离

代数距离(algebraic distance)，我们在(1.7)中尝试去最小化的$||\mathbf{A}\mathbf{h}||$，我们把$ϵ=\mathbf{A}\mathbf{h}$称之为残留向量(residual vector)，并且定义代数距离为：
$$d_{\mathrm{a}\mathrm{l}\mathrm{g}}({\mathbf{x}}_i^{\prime },H{\mathbf{x}}_i{)}^2=||{ϵ}_i|{|}^2=||\left[\begin{array}{ccc}{0}^{\mathrm{T}}& -w_i^{\prime }{\mathbf{x}}_i^{\mathrm{T}}& y_i^{\prime }{\mathbf{x}}_i^{\mathrm{T}}\\ w_i^{\prime }{\mathbf{x}}_i^{\mathrm{T}}& 0^{\mathrm{T}}& x_i^{\prime }{\mathbf{x}}_i^{\mathrm{T}}\end{array}\right]\mathbf{h}|{|}^2\text{\hspace{1em}(1.8)}$$
我们发现，每一对的匹配点都对应着一个代数距离，这个代数距离没有任何几何上或者统计上的意义，只是一个数值而已。具体点，我们有：
$$d_{\mathrm{a}\mathrm{l}\mathrm{g}}({\mathbf{x}}_1,{\mathbf{x}}_2{)}^2=a_1^2+a_2^2，其中\mathbf{a}=(a_1,a_2,a_3)={\mathbf{x}}_1\times {\mathbf{x}}_2\text{\hspace{1em}(1.9)}$$
考虑到所有的匹配点集，我们对其求和有：
$$\sum _i{d}_{\mathrm{a}\mathrm{l}\mathrm{g}}({\mathbf{x}}_i^{\prime },H{\mathbf{x}}_i{)}^2=\sum _i||{ϵ}_i|{|}^2=||\mathbf{A}\mathbf{h}|{|}^2=||ϵ|{|}^2\text{\hspace{1em}(1.10)}$$
代数距离没有几何含义，并且最小化代数距离通常给出的解并不够好，但是其有个很好的性质就是其是线性的，因此有唯一的一个解，并且计算起来很容易，可以作为其他更为复杂的非线性几何损失的初始化条件。

几何距离

在讨论几何距离之前，我们要明晰三种不同的概念：

1. $\mathbf{x}$表示在图像上的实际测量坐标结果，比如某个像素点的坐标位置。因为存在某些成像上的误差，可能实际成像和理论应该的成像位置不一致的情况，当然理论的成像位置我们并不知道，我们能测量出的一般只是$\mathbf{x}$。
2. $\hat{\mathbf{x}}$表示某个模型对该点的估计值。
3. $\bar{\mathbf{x}}$表示实际实体点的理论真实值，这个通常不能被直接测量出来。

---

在一张图像上的误差，迁移误差：

如果我们假设在第一张图像上，其测量到的点不存在误差，也就是说假设第一张图上有$\mathbf{x}=\bar{\mathbf{x}}$，那么我们只需要考虑第二张图像的误差即可。一般情况下，这种情况当然不现实，这个我们在上文讨论过，因为成像误差，实际的成像位置和真正理论上的成像位置有所偏移。但是我们这个假设在某些情况下是可以接受的，比如我们现在对相机进行矫正（calibration，也即是计算相机的内参数和外参数[11]），我们会使用一种称之为矫正图样（calibration pattern）的标定板，如Fig 1.3所示，在这种标定板上交叠着黑白色的方块，其交叠点清晰，模式明显，如Fig 1.4所示。因此可以认为这些交叠的角点的成像位置和理论成像位置一致，因此我们这个假设就有用武之地了。注意，在这个情况中，我们的一个平面是标定板，一个平面是相机的成像平面，我们在试图寻找标定板角点到相机成像平面的单应性矩阵。

Fig 1.3 可以作为矫正图样的标定板，其必须保证完全的平面，并且图样模式清晰明显，因此每个角点（黑色图样和白色图样的交叠点）清晰，可以认为是成像位置和实际位置没有误差。

Fig 1.4 标定板的角点模式非常明显，容易被程序自动识别，并且精度非常高。

考虑到这种假设合理的情况，我们设计出所谓的最小化 迁移误差(transfer error)，公式表示如(1.11)所示
$${\mathcal{E}}_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{s}\mathrm{f}\mathrm{e}\mathrm{r}}=\sum _i\mathrm{d}({\mathbf{x}}_i^{\prime },H{\bar{\mathbf{x}}}_i{)}^2\text{\hspace{1em}(1.11)}$$
注意到其中的$\mathrm{d}(\cdot )$是欧几里德距离。这个公式其实就是在描述如果在知道了单应性矩阵$H$的情况下，将第一张图像的像点通过单应性矩阵投影到第二张图像上后得到投影点$H{\bar{\mathbf{x}}}_i$，计算实际的成像点${\mathbf{x}}_i^{\prime }$与之的欧式距离。

注意，这里的欧式距离$\mathrm{d}(\mathbf{x},\mathbf{y})$其中是对$\mathbf{x},\mathbf{y}$中的非齐次坐标进行计算的，也就是说如果$\mathbf{x}=\{x_1,x_2,x_3\},\mathbf{y}=\{y_1,y_2,y_3\}$，其中$x_3,y_3$是齐次分量，不参与欧式距离计算，因此实际的欧式距离为：
$$\mathrm{d}(\mathbf{x},\mathbf{y}{)}^2=(x_1-x_2{)}^2+(y_1-y_2{)}^2\text{\hspace{1em}(1.12)}$$
总而言之，最后有：
$$\hat{H}=\arg \underset{H}{\min }{\mathcal{E}}_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{s}\mathrm{f}\mathrm{e}\mathrm{r}}\text{\hspace{1em}(1.13)}$$

---

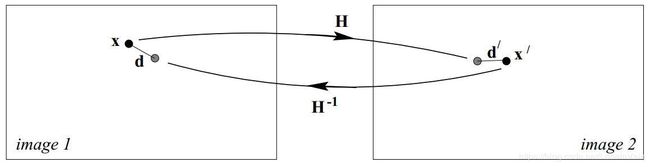
对称迁移误差：

然而更为通用且实际的方法，是考虑所谓的对称迁移，也就是将第一张图像上的像点投射到第二张图像，计算误差${\mathcal{E}}_1$；相反地，将第二张图像上的像点投影到第一张图像，计算误差${\mathcal{E}}_2$，相加两个误差得到最后的对称迁移误差$\mathcal{E}={\mathcal{E}}_1+{\mathcal{E}}_2$。公式表达如(1.14)
$$\mathcal{E}=\sum _i\mathrm{d}({\mathbf{x}}_i,H^{-1}{\mathbf{x}}_i^{\prime }{)}^2+\mathrm{d}({\mathbf{x}}_i^{\prime },H{\mathbf{x}}_i{)}^2\text{\hspace{1em}(1.14)}$$
最后的优化结果如：
$$\hat{H}=\arg \underset{H}{\min }\mathcal{E}\text{\hspace{1em}(1.15)}$$
整个过程的图示如Fig 1.5所示。

Fig 1.5 对称迁移误差的过程，进行两张图像之间像点的互相投影，并且计算误差。

---

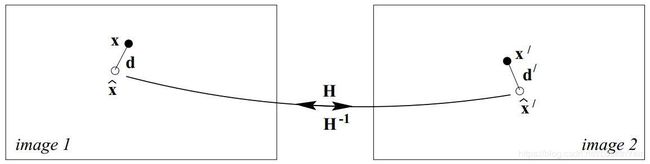
重投影误差：

我们从式子(1.14)和Fig 1.5中发现，其实我们的投影点和实际点并不是完全匹配的，因为我们的观察点都是带噪声的，并不是实际理论上的完美的点，因此即便通过单应性矩阵它们也不会完全的重合。我们可以考虑一种这种情况，假设我们通过匹配点集${\mathbf{x}}_i\leftrightarrow {\mathbf{x}}_i^{\prime }$，我们能推算出其在现实中的实际实体点${\mathbf{X}}_i$，然后通过投影，可以得到完美的一个匹配对${\hat{\mathbf{x}}}_i\leftrightarrow {\hat{\mathbf{x}}}_i^{\prime }$，其中有${\hat{\mathbf{x}}}_i^{\prime }=H{\hat{\mathbf{x}}}_i$。当然这里的实体点并不需要显式地进行估计，我们只需要如式子(1.16)所示地设计误差函数即可：
$$\begin{gathered} \mathcal{E}=\sum _i\mathrm{d}({\mathbf{x}}_i,{\hat{\mathbf{x}}}_i{)}^2+\mathrm{d}({\mathbf{x}}_i^{\prime },{\hat{\mathbf{x}}}_i^{\prime }{)}^2 \\ s.t.{\hat{\mathbf{x}}}_i^{\prime }=\hat{H}{\hat{\mathbf{x}}}_i,\forall i\text{\hspace{1em}(1.16)} \end{gathered}$$
最小化误差，有：
$$\hat{H}=\arg \underset{H}{\min }\mathcal{E}\text{\hspace{1em}(1.17)}$$
因为这个过程需要重新投影，得到一个新的估计的辅助匹配对，因此称之为重投影误差(reprojection error)。整个过程如图Fig 1.6所示。对比Fig 1.5和Fig 1.6，我们能发现，我们在重投影过程中，是充分考虑了每张图的像素点的位置误差的。

Fig 1.6 重投影误差

---

Reference

[1]. https://blog.csdn.net/LoseInVain/article/details/104533575

[2]. https://blog.csdn.net/LoseInVain/article/details/102739778

[3]. https://blog.csdn.net/LoseInVain/article/details/103369203

[4]. https://blog.csdn.net/LoseInVain/article/details/102632940

[5]. https://blog.csdn.net/LoseInVain/article/details/102665911

[6]. https://blog.csdn.net/LoseInVain/article/details/104533575

[7]. Hartley R, Zisserman A. Multiple view geometry in computer vision[M]. Cambridge university press, 2003.

[8]. https://blog.csdn.net/LoseInVain/article/details/102756630

[9]. https://blog.csdn.net/LoseInVain/article/details/102883243

[10]. https://blog.csdn.net/LoseInVain/article/details/102739778

[11]. https://blog.csdn.net/LoseInVain/article/details/102632940