Object Detection中的mAP
前言
指标很重要,合适的指标更是重中之重。mean Average Precision, mAP是常见的评估机器学习模型性能的指标,其在物体检测任务中也有着广泛地应用,是诸多Object Detection任务的主要评估指标,本文总结一些关于mAP的理解。如有谬误,请联系指出,本文参考[1,2]。
注: mAP或者AP在物体检测和信息检索中,其定义有所不同,本文特定在物体检测场景中的定义。
精准率和召回率
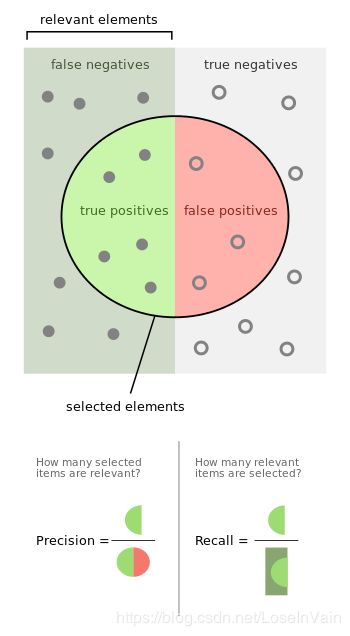
我们在[3]一文中介绍过一些常见的评估指标,其中就包括了精准率(precision)和召回率(recall),这里简单回顾下。这两个指标一般都是用在二分类问题,也就是只有两个类别需要预测,分别称之为正类(positive)或者负类(Negative),如果一个模型将真实标签为正类的样本预测为正类,那么称之为TP,True Positive,如果将其预测为负类,那么称之为FN,False Negative;如果一个模型将真实标签为负类的样本预测为正类,那么称之为FP,False Positive,如果将其预测为负类,那么称之为TN,True Negative。那么这样就遍历了二分类中的所有可能情况。那么我们接下来定义精准率和召回率,数学形式如:
P r e c i s i o n = T P T P + F P R e c a l l = T P T P + F N (1.1) \begin{aligned} \mathrm{Precision} &= \dfrac{TP}{TP+FP} \\ \mathrm{Recall} &= \dfrac{TP}{TP+FN} \end{aligned} \tag{1.1} PrecisionRecall=TP+FPTP=TP+FNTP(1.1)
其中,精准率的含义是:预测为正类并且预测正确的样本,占整个预测为正类样本(包括预测正确和错误)的比例,召回率的含义是:预测为正类且预测正确的样本,占整个数据集中真实标签为正类的比例。精准率高代表模型预测百发百中,可靠性高;召回率高表示模型不会漏了数据集中的任何一个正类。
为什么要引入这两种指标呢,我们举个例子,加入一个图片中有10个苹果需要被模型检测出来,而模型只是检测出来了其中的5个,并且都检测对了,那么如果单从精准率来看,这个模型的确靠谱,但是其漏掉了5个苹果目标的检测,这个在某些应用场景中可能就不那么可靠了,因此我们通常需要综合精准率和召回率来去考虑一个模型是否是靠谱的。精准率和召回率的计算可视化见Fig 1.1。
当然,考虑结合这两种指标有很多方式,最简单的可以考虑这两个指标的调和平均数,这样我们得到了F1指标,定义为:
F 1 s c o r e = 2 1 P r e c i s i o n + 1 R e c a l l = 2 × P r e c i s i o n × R e c a l l P r e c i s i o n + R e c a l l (1.2) \mathrm{F1 \ score} = \dfrac{2}{\dfrac{1}{\mathrm{Precision}}+\dfrac{1}{\mathrm{Recall}}} = 2 \times \dfrac{\mathrm{Precision} \times \mathrm{Recall}}{\mathrm{Precision} + \mathrm{Recall}} \tag{1.2} F1 score=Precision1+Recall12=2×Precision+RecallPrecision×Recall(1.2)
然而这个指标对于物体检测来说还是过于粗糙了,比如虽然模型对于某些物体判断类别的确错了(也就是Top 1虽然错了),但是其Top K可能能涵盖我们的目标物体类别,而F1指标并没有考虑到这种对检测结果排序,因此对于模型的评估粒度太粗糙。我们为了更加综合地考虑,引入了Average Precision,AP的概念,这个也就是我们本文的重点。
注: AP的定义不止一个,我们接下来会介绍好几类型的AP,要视不同的场景进行应用。
Average Precision
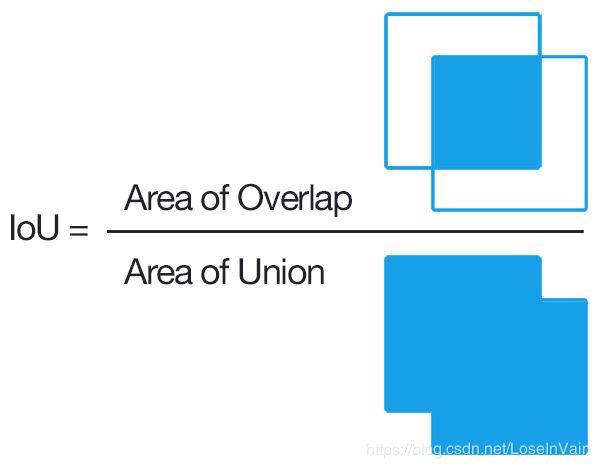
不过说到底,AP是在二分类任务中定义的,而物体检测,我们需要对物体的图片空间位置和物体类别进行检测分类,乍看一下不像是一个二分类任务,那么我们需要对其进行一定的演化。给定一个训练样本,我们会有其样本中的物体检测框的位置(我们称之为Ground Truth)和物体的类别信息,那么对于一个模型的检测输出结果来说,其和Ground Truth之间会存在一定的重合,如图Fig 1.2所示。我们可以求出检测输出结果和其Ground Truth的重合大小,我们把这个重合大小定义为IoU (Intersection of Union),具体见Fig 1.3所示,其计算很简单。
由此,我们可以定义TP,FP,FN了。
- TP,True Positive: 当 I o U > λ \mathrm{IoU} > \lambda IoU>λ时我们把预测称之为TP,其中 λ \lambda λ是一个从0到1的阈值。如下图所示。

- FP,False Positive: 当 I o U < λ \mathrm{IoU} < \lambda IoU<λ,或者出现多个重复的检测框时,我们称之为FP。IoU小于阈值或者甚至 I o U = 0 \mathrm{IoU}=0 IoU=0我们都容易理解,但是出现重复检测框,我们可以参考下图中的中间图,我们多个检测框都包含了同一个物体,这种情况下,我们只计算其中某一个的检测框,而其他的计算为FP(通常这种情况下用非极大抑制进行排除)。

- FN, False Negative: FN同样有两种情况,第一是压根就没有对某个物体的检测框,如下图所示。

第二种情况是,虽然有检测框而且 I o U > λ \mathrm{IoU} > \lambda IoU>λ,但是对其检测框的分类却错了,这个时候同样计为FN。如下图所示,把人误认为了马。

那么对于某个给定的类别(比如检测图像中的人),我们就可以通过TP,FP,FN去计算精准率和召回率了。我们接下来给出Average Precision的定义,不过在此之前,我们用一个简单的例子去进行导出这个概念。
假定我们对一个图像上的五个苹果进行物体检测,我们把阈值 λ = 0.5 \lambda =0.5 λ=0.5固定下来,然后对每个模型输出的检测框的类别可靠性(也就是模型输出的概率值,比如softmax层输出的概率值,具体要根据模型的特点指定)进行降序(也就是可靠性高的排前面),那么我们就有了以下的表:

其中第二列表示这个模型输出检测框是否 I o U > 0.5 \mathrm{IoU} > 0.5 IoU>0.5,符合条件的称之为预测正确,否则是错误。第三列表示精准率,第四列为召回率,以第三行的结果为例子,我们考虑在第三行之前一共有三个检测结果,而正确了两个,那么其精准率为 2 / 3 = 0.67 2/3=0.67 2/3=0.67,我们一共有五个苹果,只检测出来了2个,那么召回率为 2 / 5 = 0.4 2/5=0.4 2/5=0.4。根据这个简单策略,我们一直计算这个表格,直到召回率出现1.0为止(不难发现,召回率是单调递增的,而精准率则是呈现出“之”字型的结构)。我们以召回率为横轴,精准率为纵轴,绘制出曲线,称之为Precision-Recall曲线,简称为PR曲线,如:
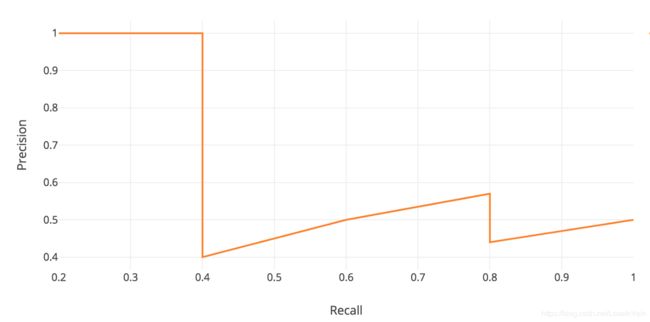
那么,通常来说,我们的广义AP(General Average Precision)定义为这个曲线的曲线下面积,数学形式为:
A P = ∫ 0 1 p ( r ) d r (2.1) \mathrm{AP} = \int_{0}^1 p(r) \mathrm{d}r \tag{2.1} AP=∫01p(r)dr(2.1)
考虑到离散形式,积分形式变成求和:
A P = ∑ 0 1 p ( r ) Δ r (2.2) \mathrm{AP} = \sum_{0}^1 p(r) \Delta r \tag{2.2} AP=0∑1p(r)Δr(2.2)
因为召回率和精准率都是0到1的值,因此AP也是0到1的值。考虑到我们这只是对某个类(比如人)进行的AP计算,如果考虑到整个数据集中的所有类别(比如人,马,狗等等),分别对每个类别求AP,然后进行平均,我们就得到了mAP(mean Average Precision)。
Interpolated Average Precision
然而,在应用中,我们经常会对这个“之”字形的曲线进行平滑,为的是避免因为排序结果的细微变化带来的AP的值的变化,为的是更鲁棒的AP结果。那么这个平滑其实也很简单,如Fig 3.1所示。我们取出某段曲线最右边的最大精准率作为之前(比如0.4-0.8段)的代表值,得到了一个递减的绿色曲线C。这个描述过于模糊,我们用数学形式表示如:
p i n t e r p ( r ) = max r ~ ≥ r p ( r ~ ) (3.1) \mathrm{p_{interp}}(r) = \max_{\tilde{r} \geq r} p(\tilde{r}) \tag{3.1} pinterp(r)=r~≥rmaxp(r~)(3.1)

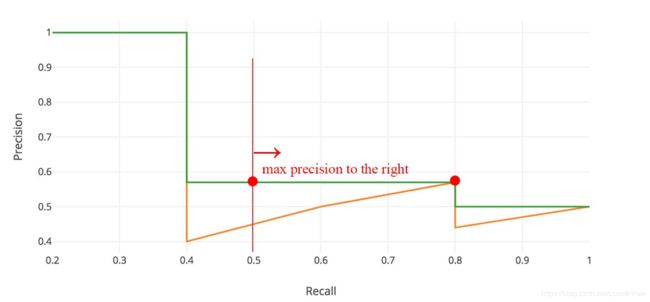
对PR曲线进行平滑只是第一步,我们还会对这个平滑后的曲线进行插值采样,比如在Pascal VOC 2008数据集上,我们对平滑PR曲线取了11个插值点(如下图的红点所示),然后我们再通过这些插值点计算AP,如:
A P = 1 11 ( A P r ( 0 ) + A P r ( 0.1 ) + ⋯ + A P r ( 1.0 ) ) (3.2) \mathrm{AP} = \dfrac{1}{11} (\mathrm{AP}_{r}(0)+\mathrm{AP}_{r}(0.1)+\cdots+\mathrm{AP}_{r}(1.0)) \tag{3.2} AP=111(APr(0)+APr(0.1)+⋯+APr(1.0))(3.2)
更正规的表达如:
A P = 1 11 ∑ r ∈ { 0.0 , ⋯ 1.0 } A P r = 1 11 ∑ r ∈ { 0.0 , ⋯ 1.0 } p i n t e r p ( r ) p i n t e r p ( r ) = max r ~ ≥ r p ( r ~ ) (3.3) \begin{aligned} \mathrm{AP} &= \dfrac{1}{11} \sum_{r \in \{0.0, \cdots 1.0\}} \mathrm{AP}_r \\ &= \dfrac{1}{11} \sum_{r \in \{0.0, \cdots 1.0\}} \mathrm{p_{interp}}(r) \\ \mathrm{p_{interp}}(r) &= \max_{\tilde{r} \geq r} p(\tilde{r}) \end{aligned} \tag{3.3} APpinterp(r)=111r∈{0.0,⋯1.0}∑APr=111r∈{0.0,⋯1.0}∑pinterp(r)=r~≥rmaxp(r~)(3.3)
- 其简化计算的前提是缺失了原先的精度。其是对实际PR曲线的模拟近似。
- 对于某些问题,不同方法的AP可能都很小,如果用这种AP计算方式,很可能会忽略掉本应该注意的小范围AP值。
因此,在2008年之后的Pascal VOC比赛,其采取了不同的AP计算方式。
Average Precision,计算AUC曲线下的面积
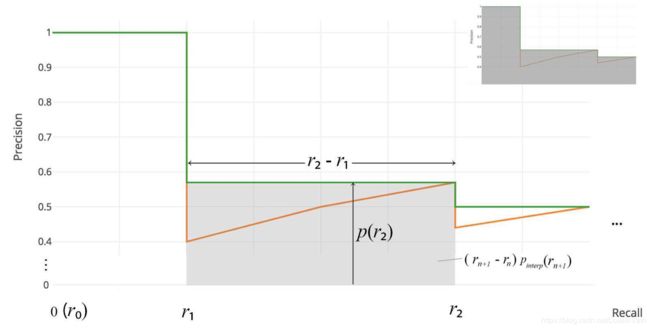
在2008年之后的VOC比赛,比如VOC2010-2012,对AP的计算方式进行了改变。此时的AP只是计算平滑后曲线的曲线下面积,如Fig 4.1所示。此时不需要任何的插值操作了。公式如:
A P = ∑ ( r n + 1 − r n ) p i n t e r p ( r n + 1 ) p i n t e r p ( r ) = max r ~ ≥ r p ( r ~ ) (4.1) \begin{aligned} \mathrm{AP} &= \sum (r_{n+1}-r_n) \mathrm{p_{interp}}(r_{n+1}) \\ & \mathrm{p_{interp}}(r) = \max_{\tilde{r} \geq r} p(\tilde{r}) \end{aligned} \tag{4.1} AP=∑(rn+1−rn)pinterp(rn+1)pinterp(r)=r~≥rmaxp(r~)(4.1)
这个定义又被称之为AUC,Area Under Curve。
Reference
[1]. https://medium.com/@jonathan_hui/map-mean-average-precision-for-object-detection-45c121a31173
[2]. https://towardsdatascience.com/breaking-down-mean-average-precision-map-ae462f623a52
[3]. https://blog.csdn.net/LoseInVain/article/details/78109029