卡尔曼滤波原理

过程方程：

X(k+1) =  A X(k) + B U(k) + W(k)               >>>>式1

量测方程：

Z(k+1) =  H X（k+1）+ V(k+1)                  >>>>式2

A和B是系统参数，对于多模型系统，他们为矩阵；H是测量系统的参数，对于多测量系统，H为矩阵。W(k)和V(k)分别表示过程和测量的噪声。他们被假设成高斯白噪声，他们的协方差 分别是Q，R。为了不失一般性，下面的讨论中将X,Z都视为矩阵，其中X是m行的单列矩阵，Z是n行的单列矩阵。

 

说明：下面的表达式中，不带前缀的量都代表实际量，其小括号里面的“k”或“k+1”代表该量是第k或第k+1时刻的实际量，如“Z(k+1)”就代表第k+1时刻的实际测量值；

带前缀“^”的量都代表预测量，如果小括号里面是“k+1|k”，就代表k+1时刻的先验预测值，如果小括号里面是“k+1|k+1”，就代表k+1时刻的后验预测值；（测量值可以通过测量得到，所以只有先验预测，没有后验预测。而实际状态值无法得知，既有先验预测，又有后验预测）

带前缀“~”的量都代表与预测值对应的偏差值。

 

实际状态值与先验预测状态值的偏差 = 实际状态值 – 先验预测状态值

~X(k+1|k)      =     X(k+1)    -      ^X(k+1|k)             >>>> 式3

 

实际测量值与先验预测测量值的偏差 = 当前测量值 - 先验预测测量值

~Z(k+1|k)  = Z(k+1)  -   ^Z(k+1|k)                                   >>>>式4

 

 

并且

先验预测测量值  =  转换矩阵H * 先验预测状态值

^Z(k+1|k) =  H ^X(k+1|k)                            >>>> 式5

 

得到测量值后，再对当前状态值X(k+1) 进行后验预测（设后验预测值为 ^Z(k+1|k+1) ） ，则后验预测值（同时也是最终预测值）的偏差为

~X(k+1|k+1)  =     X(k+1)    -      ^X(k+1|k+1)                 >>>>式6

 

 

为了得到当前状态值X(k+1)， 根据式3，需要：

X(k+1) =  ^X(k+1|k)  + ~X(k+1|k)                        >>>> 式7

上式中，我们可以通过卡尔曼公式1（见附注2）计算出^X(k+1|k)，但我们无法得知实际状态值X(k+1)，因而~X(k+1|k) 也无法得知。我们最终的目的是得出一个比较接近实际状态值X(k+1)的滤波值^X(k+1|k+1)，根据式7，只要能准确的估计出~X(k+1|k)即可。

~X(k+1|k)本身虽无法得知，但~Z(k+1|k) 却可以通过测量得到，而且它们二者存在一定的相关性。不妨再设存在一个矩阵K（m行n列矩阵），能使得

 ~X(k+1|k) = K * ~Z(k+1|k)                                        >>>>式8

那么最终的预测任务其实就是找到K。由于~X(k+1|k)和~Z(k+1|k)都是单列矩阵，因此不难看出，满足式8的矩阵K应有无穷多个。矩阵K中第i行第j列反映了量测变量偏差矩阵~Z(k+1|k)的第j个元素对状态变量偏差矩阵~X(k+1|k)的第i个元素的贡献。因此矩阵K的物理意义很明显，K的第i行第j列的元素表示：对于第i个待测的状态量来说，第j个测量仪器测到的偏差的可信度。某个测量值对应的可信度越高，滤波器越“相信”该测量值。

 

既然满足条件的K有无穷多个，那应该使用哪个K呢？实际上，我们并不知道~X(k+1|k)的值，所以也就无法直接计算出K，而只能通过某种方法找到一个Kg，使得将Kg带入式8后，等号两边的差（的平方）的期望尽可能小。

我们最终的预测值或滤波值是后验预测值^X(k+1|k+1)，因此最后的预测也应使 ~X(k+1|k+1) 的期望为0且方差最小（这与让8式两端的差最小是一致的，下面的式9体现了这一点），这样预测值才最可靠。下面详细说明。

 

^X(k+1|k+1) =  ^X(k+1|k) + Kg * ~Z(k+1|k)        （后验预测的状态值）

~X(k+1|k+1)  =     X(k+1)    -      ^X(k+1|k+1)    （后验预测的偏差）

 

~X(k+1|k+1)  =                   X(k+1)                         -             ^X(k+1|k+1)  

                     =     ( ^X(k+1|k)  +  ~X(k+1|k) ) -      (  ^X(k+1|k) + Kg * ~Z(k+1|k)  )

                     =                   ~X(k+1|k)                    -             Kg * ~Z(k+1|k)

                                                                                                         >>>>式9

 

~Z(k+1|k)       =                   Z(k+1)                         -             ^Z(k+1|k)

                     =     (  H X（k+1）+ V(k+1)  )              -      (  H ^X(k+1|k)  )

                     =     H (  X（k+1）-^X(k+1|k)  )  + V(k+1)

                     =     H ~ X(k+1|k)  + V(k+1)                                     >>>>式10

 

接下来的分析中，为了更直观的说明卡尔曼滤波的原理，我们用几何方法来解释。这时，~X和~Z矩阵中的每个元素应看做向量空间中的一个向量而不再是一个单纯的数。这个向量空间（统计测试空间）可以看成无穷多维的，每一个维对应一个可能的状态。~X和~Z矩阵中的每个元素向量都是由所有可能的状态按照各自出现的概率组合而成（在测量之前，~X和~Z 的实际值都是不可知的）。~X和~Z中的每个元素向量都应是0均值的，他们与自己的内积就是他们的协方差矩阵。我们无法给出~X和~Z中每个元素向量的具体表达，但我们通过协方差矩阵就可以知道所有元素向量的模长，以及相互之间的夹角（从内积计算）。

为了方便用几何方法解释，我们假设状态变量X是一个1行1列的矩阵（即只有一个待测状态量），而量测变量Z是一个2行1列的矩阵（即有两个测量仪器，共同测量同一个状态量X），也就是说，m=1，n=2。矩阵X中只有X[1]一项，矩阵Z中有Z[1]和Z[2]两项。Kg此时应是一个1行2列的矩阵，两个元素分别记作Kg1 和 Kg2 。H和V此时应是一个2行1列的矩阵。

将矩阵表达式9和10按元素展开：

~X(k+1|k+1)[1]    =     ~X(k+1|k)[1]              -      (Kg1 * ~Z(k+1|k)[1] + Kg2 * ~Z(k+1|k)[2] )                                                      >>>> 式9i

~Z(k+1|k)[i]   =     H[i] ~ X(k+1|k)     +     V(k+1)[i]                                   >>>>式10i

 

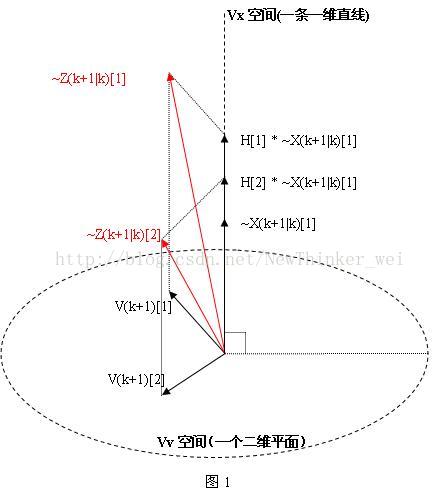
~X(k+1|k) 中各个元素（向量）的线性组合可以产生一个m维或更低维的向量子空间Vx，这里，按照我们的假设，m=1，所以Vx应是一维的； 同时V(k+1)中的各个元素（向量）的线性组合也可以产生一个n维或更低维的向量子空间Vv，这里，按照我们的假设，n=2，所以Vv应是二维的。由于V(k+1)中的每一项与~X(k+1|k)中的每一项都不相关（见附注1），故这两个子空间相互垂直。如下图所示。式10i所体现的~Z(k+1|k)[i]、H[i]~ X(k+1|k)、V(k+1)[i]  三者之间的几何关系，也在下图中描绘了出来。

 

 

 

 

 

从上图中可以看出，~Z(k+1|k)中各个元素（向量）的线性组合也可以产生一个n维或更低维的向量子空间Vz，这里已假设n=2，所以Vz是一个二维的平面，就是上图中两条红色的线所构成的平面。

  

 

图2中（注意此图中的椭圆代表的是Vz空间，而图1中则代表Vv空间，二者不一样），粉色的向量就是Kg1 * ~Z(k+1|k)[1] + Kg2 * ~Z(k+1|k)[2] ， 记此粉色向量为 Y ，Y为~Z(k+1|k)[1]和~Z(k+1|k)[2]线性组合而成，它始终在子空间Vz中。根据式9i，~X(k+1|k+1)[1] 等于~X(k+1|k)[1]和Y的差向量，为使~X(k+1|k+1)[1]长度最短（协方差最小），Kg的选取应使得~X(k+1|k+1)[1]垂直于Vz空间。

通过先验预测的协方差矩阵（见卡尔曼公式2），可以得到~X(k+1|k)中各个元素的模长以及彼此间的夹角。这是因为协方差矩阵中的第i行第j列其实就代表了~X(k+1|k)中第i个元素向量与第j个元素向量的内积。

通过测量可以得到新息协方差（见卡尔曼公式3的分母部分），进而可以知道~Z(k+1|k)中各个元素的模长以及彼此间的夹角。

通过已知的量测噪声协方差矩阵R，可以得出V(k+1) 中各个元素的模长以及彼此间的夹角。

最后根据~X(k+1|k+1)[1]与Y垂直以及图1中所示的几何关系，用高中学的立体几何和向量知识就可以求得两个Kg的值了。如果将向量的内积都用协方差矩阵表示，就会发现，我们最后求得的Kg，其实就是卡尔曼公式3。

 

（上面讨论的是较低次的卡尔曼滤波，只有一个待测量，两个测量仪器。这种情况还是比较常见的，比如倾角测量系统中，我们用加速度计和陀螺仪共同测量倾角。对于更高次的卡尔曼滤波，X和Z都是多行矩阵时，用几何方法已经无法直观解释，只能用矩阵分析的方法证明。求解Kg的详细过程参考 《卡尔曼滤波器及其应用基础》国防工业出版社敬喜 编 ）

 

卡尔曼滤波的核心过程，就是求解能使得

E { ~X(k+1|k+1) ’ *  ~X(k+1|k+1) }

取最小值的Kg增益矩阵的过程，~X(k+1|k+1)’代表的是~X(k+1|k+1)的转置（这里~X(k+1|k+1)中的元素代表数值，不是向量）。前面已经提到过，卡尔曼增益矩阵Kg中的元素，都代表测量仪器测到的偏差的可信度，或者叫估计权重。

 

 

 

 

 

 

 

附注1：

 

(a).   v(k+1)中的每一项与~X(k+1|k)中的每一项都不相关

 

~X(k+1|k)  =            X(k+1)        -         ^X(k+1|k)

          =           X(k+1)         -  ( A ^X(k|k)  +  B U(k)  )

          = ( A X(k) + B U(k) + W(k) )   -   (  A X(k)  +  B U(k)  -  A ~X(k|k) )

         =         W(k)   +   A ~X(k|k)

         =         W(k)   +   A (  ~X(k|k-1)  -  Kg(k)* ~ Z(k|k-1)  )  -----这一步利用了式9

                =                W(k)   +   A (  ~X(k|k-1)  -  Kg(k)* ( H ~X(k|k-1) + v(k) )  )             ------这一步利用了式10

                =                W(k)   -  A Kg(k) *v(k)  +  A ( I - Kg(k) * H )  ~X(k|k-1)

上式最后一行出现了~X(k|k-1)，可见~X(k+1|k)可以递归表示。而且递归式中的过程噪声W(k)与v(k+1)不相关，同时由于 v本身是白噪声，所以 v(k+1)与v(k)亦不相关（白噪声的自相关是δ函数），因此通过递推式可以判断v(k+1)与~X(k+1|k)不相关。

 

 

(b).  w(k+1)中的每一项与~X(k+1|k+1)中的每一项都不相关，w(k+1)中的每一项与~X(k+1|k)中的每一项都不相关。

~X(k+1|k+1)  =            X(k+1)        -         ^X(k+1|k+1)

          = (  ^X(k+1|k) + ~X(k+1|k)  )   -   ( ^X(k+1|k) + Kg(k+1)*~Z(k+1|k) ) 

          =             ~X(k+1|k)       -       Kg(k+1)*~Z(k+1|k)

          =             ~X(k+1|k)       -     Kg(k+1)* (  H ~X(k+1|k) + v(k+1)   ) 

          =            - Kg(k+1)* v(k+1)  +   ( I - Kg(k+1) * H ) ~X(k+1|k)

我们已经知道w(k+1)与v(k+1)不相关，因此只要~X(k+1|k+1)与上式的第二项也不相关，就说明结论(b)成立。根据(a)中的结论，~X(k+1|k)的递归展开式中出现的 v(k) ，w(k) ， v(k-1)，w(k-1)等等，显然 w(k+1)与 v (m=k，k-1……) 都不相关，另外，由于w(k+1)的自相关为δ函数，因此w(k+1)与 w(m=k，k-1……) 也不相关，也就得出w(k+1)与~X(k+1|k) 不相关。

进而可知，w(k+1)与~X(k+1|k+1)不相关。

 

 

正是因为 (a) (b)中的两个不相关，卡尔曼公式中的预测协方差矩（卡尔曼公式(2)）和新息协方差矩阵（卡尔曼公式(3)中的“分母”部分）才可以是简单的加式。

 

 

 

附注2：卡尔曼滤波的五个公式

 

先验预测值与先验预测协方差矩阵的计算。求解协方差时，都认为预测值的期望是实际值。因此，^X(k+1|k)的协方差矩阵同样也是 ~X(k+1|k) 的协方差矩阵，又因为偏差~X(k+1|k)的期望是0，因此协方差矩阵反映了~X(k+1|k)在向量空间中的模长。注意，协方差矩阵都是对称矩阵。

X(k+1|k)=A X(k|k)+B U(k)                    (1)

P(k+1|k)=A P(k|k) A’+Q(k)                   (2)

 

卡尔曼增益矩阵的计算。量测预测值为

Z(k+1|k) = H X(k+1|k)

新息协方差见公式（3）中的“分母”部分。量测预测值的期望是实际量测值。因此，^Z(k+1|k)的协方差矩阵同样也是 ~Z(k+1|k) 的协方差矩阵，又因为偏差~Z(k+1|k)的期望是0，因此协方差矩阵反映了~Z(k+1|k)在向量空间中的模长。

Kg(k+1)= P(k+1|k) H’/ (H P(k+1|k) H’ + R(k+1)) (3)

 

 

后验预测值与后验预测协方差矩阵的计算

X(k+1|k+1)= X(k+1|k)+Kg(k+1) (Z(k+1)-H X(k+1|k)) (4)

P(k+1|k+1)=（I-Kg(k+1) H）P(k+1|k)          (5)