LeetCode 第135场周赛
5051. 有效的回旋镖
回旋镖定义为一组三个点,这些点各不相同且不在一条直线上。
给出平面上三个点组成的列表,判断这些点是否可以构成回旋镖。
示例 1:
输入:[[1,1],[2,3],[3,2]]
输出:true
示例 2:
输入:[[1,1],[2,2],[3,3]]
输出:false
提示:
points.length == 3points[i].length == 20 <= points[i][j] <= 100
判断三点是否共线,只需判断三点围成的三角形面积是否为0
a r e a A B C = 1 2 A B ⃗ × A C ⃗ = 1 2 ∣ A B ⃗ ∣ ⋅ ∣ A C ⃗ ∣ s i n A = 1 2 { ( x 2 − x 1 ) ( y 3 − y 1 ) − ( y 2 − y 1 ) ( x 3 − x 1 ) } areaABC= \frac{1}{2}\vec{AB} \times \vec{AC} =\frac{1}{2} |\vec{AB}|·|\vec{AC}|sinA =\frac{1}{2}\{(x_2 - x_1)(y_3-y_1)-(y_2-y_1)(x_3-x_1)\} areaABC=21AB×AC=21∣AB∣⋅∣AC∣sinA=21{(x2−x1)(y3−y1)−(y2−y1)(x3−x1)}
或者直接计算叉积(大概这么个意思)
A B ⃗ × A C ⃗ = ∣ e 1 ⃗ e 2 ⃗ e 3 ⃗ x 1 x 2 x 3 y 1 y 2 y 3 ∣ = ( x 2 y 3 − y 2 x 3 ) e 1 ⃗ − ( x 1 y 3 − y 1 x 3 ) e 2 ⃗ + ( x 1 y 2 − y 1 x 2 ) e 3 ⃗ \vec{AB}\times\vec{AC}=\left|\begin{array}{ccc}\vec{e_1}&\vec{e_2}&\vec{e_3} \\ x_1&x_2&x_3\\y_1&y_2&y_3\end{array}\right|=(x_2y_3-y_2x_3)\vec{e_1}-(x_1y_3-y_1x_3)\vec{e_2}+(x_1y_2-y_1x_2)\vec{e_3} AB×AC=∣∣∣∣∣∣e1x1y1e2x2y2e3x3y3∣∣∣∣∣∣=(x2y3−y2x3)e1−(x1y3−y1x3)e2+(x1y2−y1x2)e3
class Solution {
public:
bool isBoomerang(vector<vector<int>>& points) {
return (points[1][0] - points[0][0])*(points[2][1] - points[0][1]) -
(points[1][1] - points[0][1])*(points[2][0] - points[0][0]) != 0;
}
};
5050. 从二叉搜索树到更大和树
给出二叉搜索树的根节点,该二叉树的节点值各不相同,修改二叉树,使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。
提醒一下,二叉搜索树满足下列约束条件:
- 节点的左子树仅包含键小于节点键的节点。
- 节点的右子树仅包含键大于节点键的节点。
- 左右子树也必须是二叉搜索树。
示例:
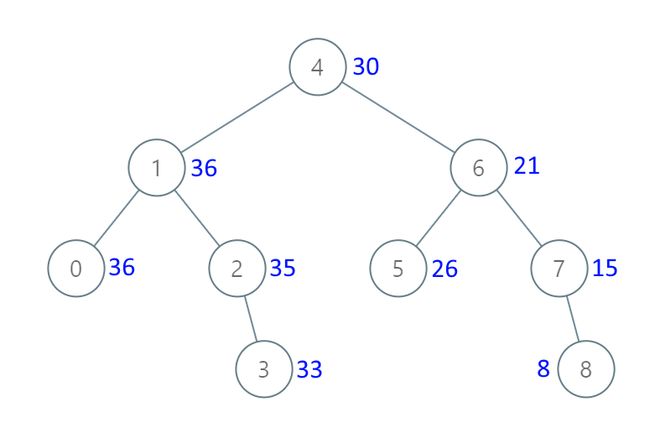
输入:[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出:[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
提示:
- 树中的节点数介于
1和100之间。 - 每个节点的值介于
0和100之间。 - 给定的树为二叉搜索树。
DFS
先右再左,直接定义一个全局变量sum进行赋值
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
int sum = 0;
void dfs(TreeNode* root)
{
if (root -> right)
dfs(root -> right);
sum += root -> val;
root -> val = sum;
if (root -> left)
dfs(root -> left);
}
TreeNode* bstToGst(TreeNode* root) {
dfs(root);
return root;
}
};