Prototypical Networks for Few-shot Learning

小样本学习的原型网络

摘要

我们为小样本分类问题提出了原型网络，分类器必须推广到训练集中没有的新类，每个新类只给出非常小的数量的样本。
原型网络在这样一个度量空间中学习：分类可以通过计算每个类的原型之间的距离来区分。
与最近的小样本学习的几种方式，它反映了一种在这种有限数据的情况下有利的更简单的归纳偏差，并且取得了非常好的结果。
我们提供的分析结果表明一些简单的设计决策能够对最近的包含复杂的架构选择和元学习的方式产生实质性的改进。
我们进一步将原型网络扩展到零样本学习并且在鸟类数据库上完成最先进的结果。

1.介绍

图1：小样本学习中的c是每个类嵌入的支持样本的均值；零样本学习中的c是嵌入的类的元数据。在每个情况下，嵌入的查询点通过softmax函数计算距离来分类。

小样本学习的任务是调整分类器去适应训练集中未见过的新类，每种类只给出非常少的样本。
一种比较天真的做法：在这些样本上重新训练模型，这会导致严重的过拟合。

虽然这种问题很困难，但是已经证明人类可以进行一次样本分类，每种类只给出一个样本，却有很高的精度。

两种取得了实质性进展的方式：
匹配网络Matching Networks：
应用注意机制的学习嵌入处理标记好的样本（支持集）来预测未标记的点（查询集）的类别。
它可以解释为应用在嵌入空间上的加权最邻分类器。
值得注意，模型在训练期间应用了称为episodes的采样小批量，被设计用来通过二次抽样分类和数据点来模仿小样本任务。
Episodes的应用使训练问题更忠实于任务环境，从而改善了泛化问题。

长期短暂记忆 LSTM：
对上述的训练方式进一步深化，提出了小样本学习的元学习方式。他们的方式包含通过训练LSTM来产生分类器的更新，给定一个episode，能够很好的推广到测试集。
LSTM元学习器对于每一个episode都训练一个自定义模型而不是对多个episodes训练单一模型。

我们通过解决过拟合的关键问题来解决小样本学习问题。
因为数据被严格限制，我们假设分类器应当拥有非常简单的归纳偏差。
我们的原型网络基于这样的思想：存在这样一个嵌入，点群聚集在每个类的单一原型周围。
为做到这一点，我们使用神经网络将输入的非线性映射到嵌入空间，并且将类的原型作为嵌入空间的支持集的均值。
然后，就可以通过简单的找到最近的类原型对嵌入的查询点进行分类。

我们采用相同的方式来处理零射击学习：每一个类都有元数据，提供了类的高级描述而不是少量的标记例子.
因此我们将元数据嵌入到共享空间中作为每一个类的原型。
和在小样本学习中一样，分类器通过对嵌入的查询节点寻找最近的类原型来进行分类。

在本文中，我们为小样本学习和零样本学习都提出了原型网络，与匹配网络在one-shot设置上建立连接，并分析了模型中的基础距离函数。

特别地，我们将原型网络与cluster相关联，以此来证明在使用bregman散度来计算距离（例如欧氏距离平方）时以类均值作为原型的正确性。
根据经验，距离的选择是至关重要的，欧氏距离远优于通常所采用的余弦相似度。
在数次基准测试任务中，我们达到了非常杰出的性能。

原型网络比最近的元学习算法更简单更有效，是一种小样本学习和零样本学习的有吸引力的实现方式。

2.原型网络

2.1 符号

在小样本分类中给出小样本支持集，N个标记的例子S；x是样例的D维特征向量，y是对应的标记。Sk表示类k的已标记样例。

2.2 模型

原型网络通过带有可学习参数的嵌入式的函数fφ（将向量从D维转换到M维）来计算每个类的M维表示向量或原型。每个原型都是该类嵌入的支持集点的平均向量。

给定一个距离函数d，原型网络基于softmax在嵌入空间中与原型之间的距离得出对于查询点x的类的分布。

通过最小化经由SGD的真类k的负对数概率J来学习。通过随机选择训练集中类的子集来组成训练episode集，然后在每个类中选择样本的子集来作为支持集剩余的作为查询集。
下面是计算训练集的损失J的伪代码：

算法：训练原型网络的episode损失计算。
输入：训练集D，其中Dk代表D包含的所有元素都属于类k。
输出：随机生成的训练episode的损失J。
为episode选择索引->选择支持样本->选择查询样本->从支持样本中计算出原型->初始化损失->更新损失

2.3 原型网络的混合密度估计

对于特定类的距离函数，称为常规Bregman散度，原型网络的算法等效于在指数族密度对于支持集执行混合密度估计。常规Bregman散度定义为：

φ是勒让德型的可微的，严格凸函数。Bregman散度的例子包括平方欧几里得距离和马哈拉诺比斯距离。

原型的计算可以支持集上的硬聚类角度来看，每个类有一个聚类，每一个支持点都被分配到对应的类的集群。已经表明，在Bregman散度下群集原型与其分配的点之间实现的最小距离是群集的均值。因此，在应用Bregman散度时给定支持集标记，等式1的原型计算得出最优的集群原型。

此外，具有参数θ和累积量函数ψ的任何正则指数族分布都可以用唯一确定的常规Bregman散度写出：

现在考虑带有参数Γ的正则指数族混合模型：

给定Γ，未标记点z的聚类分配y的推导为：

对于每个类一个集群的等加权混合模型，群集分配的推导等价于查询类的推导。在这种情况下，原型网络有效地执行混合密度推导，其中指数族分布由dψ决定。
因此，距离的选择决定了在嵌入空间中类条件数据分布的建模假设。

2.4 重新解释为线性模型

简单分析有助于了解学习分类器的本质。当我们使用欧几里得距离时，欧几里得下的模型等效于特定参数化的线性模型。要看到这一点，将术语扩展到指数中：

等式7中的首项关于类k是常量，因此它不影响softmax概率。我们可以将剩余的项写成线性模型：

在这项工作中，我们主要关注欧几里得距离（对应于球面高斯密度）。我们的结果表明欧几里得距离是一个有效的选择虽然其与线性模型等价。我们假设这是因为所有所需要的非线性都可以在嵌入的函数中学习。实际上，这是现行的神经网络分类系统所使用的方法。

2.5 与匹配网络的比较

在小样本学习情境下原型网络与匹配网络不同，在于它在一次学习情况下具有等效性。匹配网络在给定支持集时得出加权最邻分类器，而原型网络在应用平方欧几里得距离时得出线性分类器。在一次样本学习情况下，因为每个类只有一个支持点，二者等价。

一个很自然的问题是每个类使用多个原型而不是一个原型是否合理。如果每个类的原型的个数是固定的且大于1，那么就需要一个划分的方案来进一步聚集类中的支持点。这已经被mensink和rippel提出了。但是这两种方法都需要一个与权重的更新分离的单独的划分阶段，而我们的方法用普通的梯度下降法就能简单的学习。

vinyals等提出了几种扩展,包括解耦支持和查询点的嵌入函数，以及使用考虑在每episode中特定点的第二级全条件嵌入（FCE）。这些同样可以合并到原型网络中，但是它增加了可学习参数的数量，并且FCE使用双向LSTM对支持集强加随机排序。相反，我们表明使用简单的设计选择就可以达到相同的性能水平，接下来会概述。

2.6 设计选择

距离度量
vinyals和ravi和larochelle使用余弦距离来应用匹配网络。然而对于匹配网络和原型网络，任何距离都是可允许的，我们发现使用平方欧几里得距离能够大大提高两者的结果。对于原型网络，我们推测这主要是由于余弦距离不是Bregman散度，因此在2.3节中讨论的混合密度估计的等价性并不成立。
episode构成
一种构造episode的直观方式，是vinyals等人所应用的，为每个类选择Nc类和Ns支持点，以便在测试时匹配预期的情况。也就是说，如果我们预期在测试时执行五种（5-way）分类和一次样本学习，那么训练episode可由Nc=5，Ns=1组成。我们发现在测试时，高的Nc或者way对于训练都是有益的。在实验中，我们在留存的验证集上训练Nc。另一种考虑，在训练和测试时间是否去匹配Nc或者shot。对于原型网络，我们发现最好使用相同的shot数进行训练和测试。

2.7 零样本学习

与小样本学习不同之处在于，零样本学习对于每个类给出类的元数据向量vk而不是给出一组训练点的支持集。这些可以预先设定，也可以从原始文本中学习。修正原型网络来解决零样本学习非常直观，我们将———简单定义为元数据向量的独立嵌入。图1显示了原型网络的零样本学习程序与小样本学习程序相关。因为元数据向量和查询点来自不同的输入域，我们发现根据经验固定原型嵌入g使有单位长度是有帮助的，然而我们不限制查询嵌入f。

3 实验

对于小样本学习，我们用Ravi和Larochelle提出的拆分在Omniglot和ILSVRC的mini版本上进行实验。对于零样本学习，我们在2011版UCSD鸟类数据库上进行试验。

3.1 Omniglot小样本分类

Omniglot是从50个字母表中收集的1623个手写字符的数据集。每一种字符有20个由不同人写的样本。我们依据Vinyals等人的程序将灰阶图像调整为2828大小并且通过旋转90度来扩充字符类数量。我们用1200个字符以及旋转之后的总共4800类作为训练集剩余的以及其旋转作为测试集。我们的嵌入架构反映了Vinyals等人所使用的架构并且由四个卷积块构成。每个块由64-滤波器33卷积，批量标准化层，ReLU非线性以及22最大池化层。当应用于2828Omniglot图像时该架构产生64维输出空间。我们使用相同的编码器来嵌入支持点和查询点。我们所有的模型都使用Adam通过SGD进行训练。我们使用10的-3次方初始学习速率并且每2000episodes将速率下调一半。除了批量标准化之外，不使用正则化。

我们使用平方欧几里得距离在1样本和5样本的情况下进行原型网络训练，训练episode包括60个类，每个类包括5个查询点。我们发现将训练样本和测试样本相匹配是有利的，并且每个训练episode使用更多的类也是有利的。我们比较各种基线，包括Neural Statistician，元学习器LSTM，MAML，以及匹配网络的微调以及非微调版本。我们对于从测试集中随机生成的1000个episodes进行计算分类准确度。结果显示在表1，根据我们的认知，结果在这个数据集上与目前最先进技术具有竞争力。

图2显示的是由原型网络训练的t-SNE可视化示例。为了更好了解其本质，我们将同一个字母表中的测试字符的子集可视化，尽管实际测试中是来自不同的字母表。尽管不同字符之间的变化非常小，网络仍然能将手写字符集群在其类的原型附近。

图2：在Omniglot数据集上使用原型网络学习的嵌入的t-SNE可视化。显示了一种测试集中的字母表（Tengwar）的子集。类原型用黑色表示，一些错误分类的字符使用红色显示，箭头指向其正确的分类。

3.2 miniImageNet小样本分类

miniImageNet数据集起初由Vinyals等人提出，来源于一个更大的ILSVRC-12数据集。他们所使用的部分是有60000个84*84的彩色图像，被分为100个类，每个类中有600个样本。为了与目前最先进的算法进行直接比较，我们使用了Ravi和Larochelle所使用的数据集。有100个类，其中64个训练类，16个验证类，20个测试类。我们根据他们的程序，在这64个训练类上进行训练，使用16个验证类来监控泛化性能。

我们使用与Omniglot相同的四个卷积块的嵌入架构，尽管由于图像尺寸增加，它会产生1600维的输出空间。我们还采用了与Omniglot相同的学习速率，并且训练直到验证损失停止增加。我们使用30-way episode进行1样本分类，20-way episodes进行5样本分类。我们将训练样本与测试样本相匹配，每个类的每个episode包含15个查询点。我们将其与Ravi和Larochelle提出的基准线进行比较，其中包含一个通过64个训练类学习的分类网络的简单的最邻方法。其他的基准线包括匹配网络（原始和FCE）和非微调设置的元学习器LSTM的两个非微调变体。因为Vinyals等人提出的微调程序并没有完全描述。正如表2所显示的，原型网络在5样本学习精度的大幅度提高达到了最先进水平。

我们进行了进一步分析，来确定距离量度以及每episode中训练类的数量对于原型网络和匹配网络的性能的影响。为了使这些方式具有可比性，我们使用了与我们的原型网络使用相同嵌入架构的匹配网络来实现。在图3中，我们对于1样本和5样本情况下的余弦距离和欧几里得距离，5-way和20-way episodes进行比较。我们发现20-way比5-way有更高的精度，并且推断20-way分类的难度使网络更好泛化，因为其使嵌入空间的模型做出更具细粒度的决策。此外，欧几里得距离比余弦距离提高了性能，这种影响对于原型网络更为明显。将类原型计算作为嵌入支持点的平均值更自然的适合欧几里得距离，因为余弦距离不属于Bregman散度。

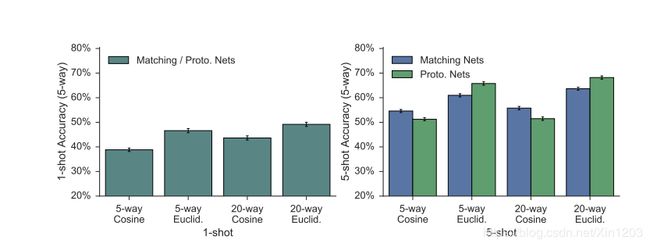
图3：比较显示了距离度量和每个episode中类的数量对于5-way分类精度的影响。x轴表示训练episode配置（way，距离，样本），y轴表示相应5-way测试的精度。误差条显示的是每600个测试episode计算中的95%置信区间。注意在1样本学习中匹配网络和原型网络是一致的。

3.3 CUB零样本分类

为了检测我们的方案对于零样本学习的适用性，我们也在UCSD鸟类数据集上进行实验，它含有200种鸟的11788个图片。我们在准备阶段密切关注Reed等人的程序。我们将他们的数据集部分分为100训练集，50验证集，50测试集。对于图像，我们应用Googlenet在原始图像和水平翻转图像的中间，左上右上，左下右下部分抽象1024维特征。在测试时，我们只使用原始图像的中间部分，对于类的元数据，我们使用CUB数据集提供的312维的连续特征向量。这些特征编码了不同种类鸟的颜色，形状，羽毛图案等。

我们在1024维图像特征和312维属性向量之上学习了一个简单的线性映射，来产生一个1024维的输出空间。对于这个数据集，我们发现应当将类原型（嵌入的属性向量）规范化为单位长度，因为属性向量来自于与图像不同的域。训练episode由50个类组成，每个类有10个查询图像。嵌入通过经由SGD的Adam进行优化，学习速率固定为10的-4次方，权重延迟10的-5次方。早期的验证损失的停止用于决定在训练和验证集进行重新训练的最佳时期数。

表3显示了与使用属性作为类的元数据的方式相比，我们获得了最先进的结果。我们将我们的方式与其他零样本学习进行比较，包括ALE，SJE等嵌入方式。我们还与最近的一种聚类方式进行比较，这种方式通过在微调的Alexnet获得的学习特征空间上训练SVM。

我们用一组更强的类元数据进行了另外的零样本实验。这些实验表明即使数据点来自于类的不同域，我们的方式也足够通用。

4 相关工作

度量学习的文献有很多，我们总结了与我们的最相关的几种。
邻域成分分析（NCA）学习马哈拉诺比斯距离来最大化在变化空间中的K-最邻（KNN）的留一法精度。
Salak和Hinton通过使用神经网络执行转换来扩展NCA。
大边缘最邻分类（LMNN）也试图优化KNN精确度，但使用了铰链损失来鼓励点的局部邻域包含其他具有相同标签的点。
DNet-KNN是另一种基于边缘的方法，它通过利用神经网络执行嵌入而不是简单的线性转换来改进LMNN。
其中，我们的方式更像是NCA的非线性扩展，我们使用神经网络来执行嵌入，我们在转换空间中基于欧几里得距离来优化softmax而不是通过边际损失。与非线性NCA最关键的不同之处在于我们直接通过类形成softmax，而不是通过计算到类的原型表示的单独的点。这允许每个类具有独立于数据点数量的简明表示，并且避免在预测时需要存储整个支持集。

我们的方案也类似于最近类均值方案，每个类被其样本的均值所表示。这种方式被改进以用来快速不经过重新训练就将新的类合并到分类器中，然而它依赖的是线性嵌入并且它是被设计用于处理新的类具有非常大的样本量的情况。相反，我们的方式利用神经网络来非线性嵌入点，并且将其与episode的训练相结合来处理小样本的情况。Mensink等人也试图将他们的方法应用于非线性分类，但是他们是通过允许每个类有多个原型。他们通过在输入空间上使用k-means在预处理步骤中找到这些原型，然后执行他们线性嵌入的多模态变体。在另一方面，原型网络不经过预处理，以端到端的方式学习非线性嵌入，产生了每个类仍然只需要一种原型的非线性分类器。另一方面，我们的方式更自然的扩展到其他距离函数中，尤其是Bregman维度。

Wen等人提出的中心损失关于面部识别的应用与我们的方式相近，但是有两个主要的不同。首先，他们将类的中心作为模型的参数来学习，而我们以每episode中的标记样本来计算原型。其次，他们将中心损失与softmax损失结合起来来防止表示坍缩为0，而我们从原型中构造softmax损失，自然可以防止这种坍缩。此外，我们的方式适用于小样本学习而不是面部识别。

一个相关的小样本学习方式是由Ravi和Larochelle提出的元学习方式。它的核心是LSTM动态和梯度下降可以高效地以相同方式编写。然后可以训练LSTM自己来训练来自给定episode的模型，其性能目标是在查询点有较好的泛化。
MAML是另一种小样本学习的元学习方案，它试图学习一种经过非常少的梯度下降步骤就能适应新数据的模型。
匹配网络和原型网络也可以看做是元学习方法的一种形式，因为它们从新的训练episode中动态的生成简单的分类器，不同之处在于它们所依赖的核心嵌入在训练之后就已经固定了。匹配网络的FCE扩展包含依赖于支持集的二级嵌入。然而，在小样本学习情况下，数据样本的非常小，简单的归纳偏差似乎运作良好，不需要为每个episode学习自定义嵌入。

与Neural Statistician一样，我们为每个类得出一个汇总的统计数据。但是我们的是一个歧视性模型，这符合我们对于小样本学习的判别性任务。

关于零样本学习，原型网络对于嵌入元数据的应用预测线性分类器的权重。DS-SJE和DA-SJE的方式也学习了图像和类元数据的深度多模态嵌入函数。与我们的不同，他们的学习使用经验的风险损失。但是他们两个都没有使用episode训练，这种训练让我们加速训练并标准化模型。

5 总结

我们提出了对于小样本学习的原型网络的简单方式，它基于这种思想：我们可以在使用神经网络学习的表示空间中使用样本的均值来表示类。通过使用episode训练，这些网络在小样本设置下表现良好。原型网络比最近的元学习方式更简单也更有效，并且即使没有为匹配网络所开发的复杂扩展（它们也能应用于原型网络），它也能产生最先进的结果。我们通过谨慎选择距离度量和修正episode的学习程序来大幅度改良性能。我们进一步演示如何将其扩展到零样本学习，并且在CUB-200数据集上实现了最先进的结果。未来工作的自然的方向是利用Bregman散度而不是欧几里得距离来应对超出球面高斯的类条件分布。我们对其进行初步探索，包括为每个类的每个维度学习方差，这没有任何实质性收获。这表明嵌入网络自身具有足够的灵活性，不需要每类额外的拟合参数。总体来说，原型网络的简单和有效使其成为一种很有前景的小样本学习方法。