数据结构与算法之美学习笔记(5~9章)
第五章 数组:为什么很多编程语言中数组都从0开始编号?
1.数组的定义
数组是一种线性表数据结构,他用一组连续的内存空间,来存储相同类型的数据
2.数组为什么可以根据下标随机访问数组元素
(这里要注意不根据下标是不能随机访问的啊)
假设一个长度为10的int型数组,会分配一块连续内存空间 1000~1039,其中,内存块首地址是1000
我们可以通过以下公式快速获取到指定下标的元素
a[i]_address = base_address + i * data_type_size
base_address 就是首地址 1000, i为我们要获取的下标,.data_type_size为每个元素的字节大小,这里int为4个字节
比如我们要找第1个元素,为1000+1*4 = 1004
这里其实可以解释为什么数组从0开始
因为如果从1开始 上面的公式就会变成
a[i]_address = base_address + (i -1)* data_type_size
CPU在执行指令的时候 还需要多执行一步减1的操作,虽然影响不大,但数组做为一个底层的数据结构,应该尽量做到优化
3.数组的插入,删除
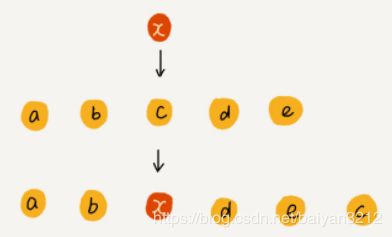
数组在插入和删除的时候会需要移动插入或删除目标位置后面的元素.这样最好情况下时间复杂度为O(1),最坏为O(n)
深入思考
但是我们换个角度看,如果换个角度,如果数组不要求保证元素的顺序性,比如在插入元素到指定下标i的时候,我们可以直接找到下标为i的原有元素然后将他放在数组最后,然后将要插入的元素直接放在空出来的i的位置.这样时间复杂度将变O(1)
同样的当我们要对数组进行多次删除时.我们可以先不进行删除,只是记录下要删除的下标,等到数组容量不够时,我们一次性进行删除.
这就有点类似我们JVM中的标记清除.
第六章 链表(上) 利用链表实现;LRU缓存淘汰机制
一.链表的分类
1.单向链表
内存块称为链表的“结点”,第一个结点叫作头结点,最后一个结点叫作尾结点,记录下个结点地址的指针叫作后继指针 next
链表的优势在于插入删除操作简单.只需要控制前后节点的改变即可时间复杂度为O(1)
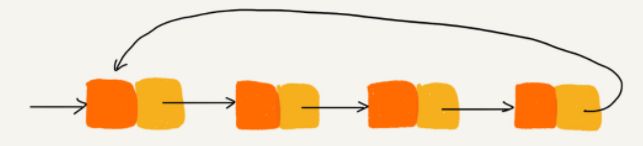
2.循环链表
循环链表是一种特殊的单链表,循环链表的尾结点指针是指向链表的头结点
3.双向链表
支持两个方向,每个结点不止有一个后继指针 next 指向后面的结点,还有一个前驱指针 prev 指向前面的结点。
双向链表相比于单向链表的优势在于,他记录了前指针,也就是可以快速的找到前面的节点,单向链表虽然删除操作快,但是前提要知道前和后节点,在已知当前节点要删除或插入位置时,还得遍历链表找到后继节点为目标节点的节点,也就是前节点,这个操作时间复杂度是O(N)
4.双向循环链表
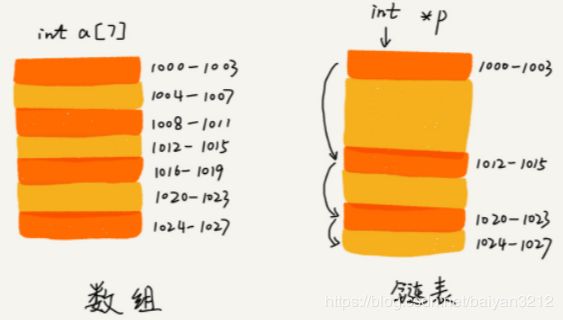
二.链表和数组的区别
两者都是线性表结构.不同点在于数组是一组连续的内存空间,而链表是一组分散的内存空间,假设内存中剩下100M 但这100M不是连续的内存空间,数组就无法存入,而链表可以存入,同时数组需要制定初始空间,设置过大会浪费内存,设置过小就需要设置新的更大空间的数组,然后将原有数组拷贝到新的数组,这个操作非常耗时,即使arrayList可以动态扩容,但是我们如果我们储存的数据大小达到1G,这个时候数组空间不足,自动扩容为1.5G,此时还需要复制拷贝,可以想象下时间耗费是多大.
数组可以根据下标快速随机访问 时间复杂度是O(1),但是链表必须遍历查询时间复杂度是O(n),反之数组插入删除的时间复杂度是O(n),链表的时间复杂度为O(1).
三.使用链表实现LUA缓存淘汰算法
LUA常见淘汰策略有3种,先进先出,最少使用,最近最少使用.
我们维护一个有序单链表,越靠近链表尾部的结点是越早之前访问的。当有一个新的数据被访问时,我们从链表头开始顺序遍历链表。
1. 如果此数据之前已经被缓存在链表中了,我们遍历得到这个数据对应的结点,并将其从原来的位置删除,然后再插入到链表的头部。
2. 如果此数据没有在缓存链表中,又可以分为两种情况:
-
如果此时缓存未满,则将此结点直接插入到链表的头部;
-
如果此时缓存已满,则链表尾结点删除,将新的数据结点插入链表的头部。
这样我们就用链表实现了一个 LRU 缓存
第七章 链表(下):如何轻松写出正确的链表代码?
*
-
单链表反转
-
链表中环的检测
-
两个有序的链表合并
-
删除链表倒数第 n 个结点
-
求链表的中间结点
第八章 栈
第九章 队列