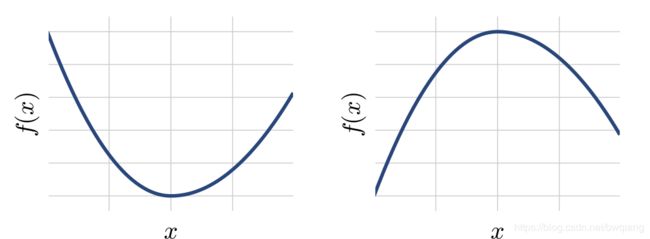机器学习中的数学（上）

  上篇博文介绍了《机器学习之支持向量机》后发现利用到了梯度、凸优化、拉格朗日对偶性等数学问题。而且凸优化是本科非数学专业学不到的科目，所以这篇博文就要和大家分享一下机器学习中常用的数学概念。

  博文重点：

• 线性代数。
• 凸优化。
• 概率论（机器学习中的数学（中））。
• 机器学习中常用的不等式（机器学习中的数学（下））。

1、线性代数

  这部分介绍一些机器学习中常用的线性代数知识点包括向量的范数和矩阵的范数及其相关性质。

1.1 向量和范数

  这一部分将通过$\mathbb{H}$来定义一个维数可能是无限的向量空间。

1.1.1 范数

定义1.1： 映射$\Phi :\mathbb{H}\to {\mathbb{R}}_{+}$被认为是$\mathbb{H}$上的范数如果它满足如下公理：

• 非负性（definiteness）：$\forall \mathbf{x}\in \mathbb{H},\Phi (\mathbf{x})=0\iff \mathbf{x}=0,\Phi (\mathbf{x})>0\iff \mathbf{x}\ne 0$；
• 同质性（齐次性）（homogeneity）：$\forall \mathbf{x}\in \mathbb{H},\forall \alpha \in \mathbb{R},\Phi (\alpha \mathbf{x})=|\alpha |\Phi (\mathbf{x})$；
• 三角不等式（triangle inequality）：$\forall \mathbf{x},\mathbf{y}\in \mathbb{H},\Phi (\mathbf{x}+\mathbf{y})\le \Phi (\mathbf{x})+\Phi (\mathbf{y})$。

对任意$p\ge 1$，$L_p$范数可以通过下述定义：

$$\forall \mathbf{x}\in {\mathbb{R}}^N,||\mathbf{x}|{|}_p=(\sum _{j=1}^N|x_j{|}^p{)}^{1/p}.$$

$L_1,L_2$和$L_{\infty }$范数是用的最多的范数，其中$||\mathbf{x}|{|}_{\infty }={\max }_{j\in [N]}|x_j|$。下述不等式都是成立的：

$$\begin{gathered} ||\mathbf{x}|{|}_2\le ||\mathbf{x}|{|}_1\le \sqrt{N}||\mathbf{x}|{|}_2 \\ ||\mathbf{x}|{|}_{\infty }\le ||\mathbf{x}|{|}_2\le \sqrt{N}||\mathbf{x}|{|}_{\infty } \\ ||\mathbf{x}|{|}_{\infty }\le ||\mathbf{x}|{|}_1\le N||\mathbf{x}|{|}_{\infty }. \end{gathered}$$

定义1.2：希尔伯特空间（Hilbert space）： 希尔伯特空间是由向量空间的内积组成的$⟨\cdot ,\cdot ⟩$，内积导出一个范数，定义如下：

$$\forall \mathbf{x}\in \mathbb{H},||\mathbf{x}|{|}_{\mathbb{H}}=\sqrt{⟨\mathbf{x},\mathbf{x}⟩}.$$

1.1.2 对偶范数（Dual norms）

定义1.3： 让$||\cdot ||$表示一个在${\mathbb{R}}^N$上的范数。与$||\cdot ||$相关的对偶范数$||\cdot |{|}_{\ast }$是如下定义：

$$\forall \mathbf{y}\in {\mathbb{R}}^N，||\mathbf{y}|{|}_{\ast }=\underset{||\mathbf{x}||=1}{\sup }|⟨\mathbf{y}\cdot \mathbf{x}⟩|.$$

对任意的$p,q\ge 1$是共轭的（conjugate）也就是$\frac{1}{p}+\frac{1}{q}=1$，则有$L_p$和$L_q$范数互为对偶范数。一般来说，$L_2$的对偶范数是$L_2$，$L_1$的对偶范数是$L_{\infty }$。

命题1.4：Hölder不等式： 让$p,q\ge 1$是共轭的，即$\frac{1}{p}+\frac{1}{q}=1$。对所有的$x,y\in {\mathbb{R}}^N$，

$$|⟨\mathbf{x},\mathbf{y}⟩|\le ||\mathbf{x}|{|}_p||\mathbf{y}|{|}_q,$$

当对于所有的$i\in [N]$时，$|y_i|=|x_i{|}^{p-1}$时，上式取等。

推论1.5：柯西-施瓦兹不等式（Cauchy-Schwarz inequality）： 对所有的$\mathbf{x},\mathbf{y}\in {\mathbb{R}}^N$，

$$|⟨\mathbf{x},\mathbf{y}⟩|\le ||\mathbf{x}|{|}_2||\mathbf{y}|{|}_2,$$当且仅当$\mathbf{x},\mathbf{y}$共线时，上式取等。

1.2 矩阵

  对于$\mathbf{M}\in {\mathbb{R}}^{m\times n}$是一个$m$行$n$列的矩阵，定义${\mathbf{M}}_{ij}$是它的第$i$行$j$列的元素。对任意$m\ge 1$，通过${\mathbf{I}}_m$表示$m$维单位矩阵。

  矩阵$\mathbf{M}$的转置是${\mathbf{M}}^{\top }$，对所有的$(i,j)$都有$({\mathbf{M}}^{\top }{)}_{ij}={\mathbf{M}}_{ji}$。对任意的两个矩阵$\mathbf{M}\in {\mathbb{R}}^{m\times n}$和$\mathbf{N}\in {\mathbb{R}}^{n\times p}$，$(\mathbf{M}\mathbf{N}{)}^{\top }={\mathbf{N}}^{\top }{\mathbf{M}}^{\top }$。

  矩阵$\mathbf{M}$的迹$\text{Tr}[\mathbf{M}]={\sum }_{i=1}^N{\mathbf{M}}_{ii}$。对任意的两个矩阵$\mathbf{M}\in {\mathbb{R}}^{m\times n}$和$\mathbf{N}\in {\mathbb{R}}^{n\times p}$，都有$\text{Tr}[\mathbf{M}\mathbf{N}]=\text{Tr}[\mathbf{N}\mathbf{M}]$成立。

  满秩矩阵$\mathbf{M}$的逆，定义为${\mathbf{M}}^{-1}$，满足$\mathbf{M}{\mathbf{M}}^{-1}={\mathbf{M}}^{-1}\mathbf{M}=\mathbf{I}$。

1.2.1 矩阵范数

  矩阵范数是定义在${\mathbb{R}}^{m\times n}$上的范数，其中$m$和$n$是矩阵的维度。许多矩阵范数满足下列次乘法性质（相容性）：

$$||\mathbf{M}\mathbf{N}||\le ||\mathbf{M}||\cdot ||\mathbf{N}||.$$

  由向量$p$范数诱导的矩阵范数如下：

$$||\mathbf{M}|{|}_p=\underset{||\mathbf{x}|{|}_p\le 1}{\sup }||\mathbf{M}\mathbf{x}|{|}_p.$$

当$p=2$时被称为是谱范数（ spectral norm），谱范数等于该矩阵的最大奇异值或者是${\mathbf{M}}^{\top }\mathbf{M}$的最大特征值的平方根：

$$||\mathbf{M}|{|}_2={\sigma }_1(\mathbf{M})=\sqrt{{\lambda }_{\max }({\mathbf{M}}^{\top }\mathbf{M})}.$$

  不是所有的范数都是向量诱导范数。Frobenius范数就是非诱导范数：

$$||\mathbf{M}|{|}_F=(\sum _{i=1}^m\sum _{j=1}^n{\mathbf{M}}_{ij}^2{)}^{1/2}.$$

显然，当$\mathbf{M}$是一个长度为$mn$的向量时，此时的$F$范数就是向量的$L_2$范数了。矩阵的$F$范数和矩阵的迹的关系：

$$⟨\mathbf{M},\mathbf{N}{⟩}_F=\text{Tr}[{\mathbf{M}}^{\top }\mathbf{N}].$$

$F$范数与矩阵$\mathbf{M}$奇异值的相关性：

$$||\mathbf{M}|{|}_F^2=\text{Tr}[{\mathbf{M}}^{\top }\mathbf{M}]=\sum _{i=1}^r[{\sigma }_i(\mathbf{M}){]}^2,$$其中$r$是$M$的秩。

  对任意$j\in [N]$，让${\mathbf{M}}_j$表示矩阵$\mathbf{M}$的第$j$列，$\mathbf{M}=[{\mathbf{M}}_1\cdots {\mathbf{M}}_n]$。对任意$p,r\ge 1$，$\mathbf{M}$的组范数（group norm ）$L_{p,r}$是：

$$||\mathbf{M}|{|}_{p,r}=(\sum _{j=1}^n||\mathbf{M}|{|}_p^r{)}^{1/r}.$$

使用最多的组范数是$L_{2,1}$范数，如下定义：

$$||\mathbf{M}|{|}_{2,1}=\sum _{i=1}^n||{\mathbf{M}}_i|{|}_2.$$

就是矩阵每列作为向量的$L_2$范数的逐一求和。

1.2.2 奇异值分解（Singular value decomposition）

  矩阵$\mathbf{M}$的秩$r$满足：$r=\text{rank}(\mathbf{M})\le \min (m,n)$。矩阵的奇异值分解如下：

$$\mathbf{M}={\mathbf{U}}_M{\mathbf{\Sigma }}_M{\mathbf{V}}_M^{\top }.$$

其中，矩阵${\mathbf{\Sigma }}_M=\text{diag}({\sigma }_1,\cdots ,{\sigma }_r)$是包含矩阵$\mathbf{M}$的非零奇异值按照递减排列的对角阵，即${\sigma }_1\ge \cdots \ge {\sigma }_r>0$。矩阵${\mathbf{U}}_M\in {\mathbb{R}}^{m\times r}$和${\mathbf{V}}_M\in {\mathbb{R}}^{n\times r}$中的列向量是矩阵$\mathbf{M}$的奇异值的左右奇异正交向量。通过${\mathbf{U}}_k\in {\mathbb{R}}^{m\times k},k\le r$来表示$\mathbf{M}$的左奇异值向量。

  投影到${\mathbf{U}}_k$的正交映射可以写成${\mathbf{P}}_{U_k}={\mathbf{U}}_k{\mathbf{U}}_k^{\top }$，并且${\mathbf{P}}_{U_k}$是对称半正定和幂等的，即${\mathbf{P}}_{U_k}^2={\mathbf{P}}_{U_k}$。矩阵$\mathbf{M}$的右奇异值向量也是一样的。

  对于$\mathbf{M}$的广义逆矩阵或者是Moore-Penrose伪逆矩阵${\mathbf{M}}^{†}$如下定义：

$${\mathbf{M}}^{†}={\mathbf{U}}_M{\Sigma }_M^{†}{\mathbf{V}}_M^{\top },$$

其中${\Sigma }_M^{†}=({\sigma }_1^{-1},\cdots ,{\sigma }_r^{-1})$，对任何$m\times m$的满秩矩阵$\mathbf{M}$，矩阵的伪逆矩阵就是矩阵的逆：${\mathbf{M}}^{†}={\mathbf{M}}^{-1}$。

1.2.3 对称正半定矩阵（Symmetric positive semidefinite (SPSD) matrices）

定义7： 一个对称矩阵是$\mathbf{M}\in {\mathbb{R}}^{m\times m}$是半正定的，当且仅当，对所有的$\mathbf{x}\in {\mathbb{R}}^m$：

$${\mathbf{x}}^{\top }\mathbf{M}\mathbf{x}\ge 0.$$
当上式严格大于零时，$\mathbf{M}$是正定的。也可以说，当且仅当一个矩阵的特征值非负时， $\mathbf{M}$是对称正半定的。下述特点对任何对称半正定矩阵$\mathbf{M}$均成立：

• 对某些矩阵$\mathbf{X}$，$\mathbf{M}$可以分解成$\mathbf{M}={\mathbf{X}}^{\top }\mathbf{X}$。
• $\mathbf{M}$的左右奇异值向量是相同的，并且$\mathbf{M}$的奇异值分解也是它的特征值分解。
• 任意矩阵$\mathbf{X}={\mathbf{U}}_X{\mathbf{\Sigma }}_X{\mathbf{V}}_X^{\top }$的奇异值分解就是两个相关的对称正半定矩阵的奇异值分解：左奇异值向量是$\mathbf{X}{\mathbf{X}}^{\top }$的特征向量，右奇异值向量就是${\mathbf{X}}^{\top }\mathbf{X}$的特征向量。并且$\mathbf{X}$的非零奇异值是$\mathbf{X}{\mathbf{X}}^{\top }$和${\mathbf{X}}^{\top }\mathbf{X}$非零特征值的平方根。
• $\mathbf{X}$的迹是它的奇异值的和，$\text{Tr}[\mathbf{M}]={\sum }_{i=1}^r{\sigma }_i(\mathbf{M})$，其中$\text{rank}(\mathbf{M})=r$。

2、凸优化（Convex Optimization）

  这一小节介绍机器学习中常用的凸优化问题。

2.1 可微和无约束最优化（Differentiation and unconstrained optimization）

  我们从一些基本的微分定义开始，这些定义是介绍费马定理和描述凸函数的一些性质所必要的准备。

定义2.1：梯度 令$f:\mathcal{X}\subseteq {\mathbb{R}}^N\to \mathbb{R}$是一个可微函数。$f$在$\mathbf{x}\in \mathcal{X}$向量处的梯度表示为$\nabla f(\mathbf{x})$并有如下定义：

$$\nabla f(\mathbf{x})=\left[\begin{array}{c}\frac{\partial f}{\partial {\mathbf{x}}_1}(\mathbf{x})\\ ⋮\\ \frac{\partial f}{\partial {\mathbf{x}}_N}(\mathbf{x})\end{array}\right].$$

定义2.2： 海森（Hessian） 令$f:\mathcal{X}\subseteq {\mathbb{R}}^N\to \mathbb{R}$是一个二阶可微函数。则$f$在$\mathbf{x}\in \mathcal{X}$处的海森矩阵是表示为${\nabla }^{2}f(\mathbf{x})$ 的 ${\mathbb{R}}^{N\times N}$的矩阵，定义如下：

$${\nabla }^{2}f(\mathbf{x})=[\frac{{\partial }^{2}f}{\partial {\mathbf{x}}_i\partial {\mathbf{x}}_j}(\mathbf{x}){]}_{1\le i,j\le N}.$$

  接下来，我们给出了无约束优化的一个经典结果。

定理2.3:费马定理（Fermat’s theorem） 令$f:\mathcal{X}\subseteq {\mathbb{R}}^N\to \mathbb{R}$是一个可微函数。如果${\mathbf{x}}^{\ast }\in \mathcal{X}$是$f$的一个局部极值，则$\nabla f({\mathbf{x}}^{\ast })=0$，也就是说，${\mathbf{x}}^{\ast }$是一个驻点（stationary point） 。

2.2 凸性（Convexity）

  这一部分将要介绍凸集和凸函数的概念。凸函数在机器学习算法的设计和分析中起着重要的作用，部分原因是凸函数的局部极小值就是全局最小值。因此，一个假设的特点是通过凸优化寻找到的局部最小值往往很好理解，而对于一些非凸优化问题可能会有大量的局部最小值没有明显特征的假设可以学习。

定义2.4：凸集 一个集合$\mathcal{X}\subseteq {\mathbb{R}}^N$被认为是凸的，如果任意两个点$\mathbf{x},\mathbf{y}\in \mathcal{X}$，区间$[\mathbf{x},\mathbf{y}]\subseteq \mathcal{X}$，满足

$$\{\alpha \mathbf{x}+(1-\alpha )\mathbf{y}:0\le \alpha \le 1\}\subseteq \mathcal{X}.$$
具体地说，在欧氏空间中，凸集是对于集合内的每一对点，连接该对点的直线段上的每个点也在该集合内。

  下面的引理阐述了在凸集上保持凸性的几种操作。这些将有助于证明本节的几个后续结果。

引理 2.5 凸集的一些操作 ：

• 令集合$\{{\mathcal{C}}_i{\}}_{i\in I}$是凸集，则集合任意部分${\bigcap }_{i\in I}{\mathcal{C}}_i$也是凸集。
• 令集合${\mathcal{C}}_1$和${\mathcal{C}}_2$是凸集，则它们的和${\mathcal{C}}_1+{\mathcal{C}}_2=\{x_1+x_2:x_1\in {\mathcal{C}}_1,x_2\in {\mathcal{C}}_2\}$也是凸集。
• 令集合${\mathcal{C}}_1$和${\mathcal{C}}_2$是凸集，则它们叉积（ cross-product）（${\mathcal{C}}_1\times {\mathcal{C}}_2$）也是凸的（叉积：$\mathbf{a}\times \mathbf{b}=|\mathbf{a}|\cdot |\mathbf{b}|\cdot \sin \theta$）。
• 凸集$\mathcal{C}$的任何投影也是凸的。

定义2.6：凸包（Convex hull） 一系列点$\mathcal{X}\in {\mathbb{R}}^N$的凸包$\text{conv}(\mathcal{X})$是包含$\mathcal{X}$的最小凸集，等价于如下定义：

$$\text{conv}(\mathcal{X})=\{\sum _{i=1}^m{\alpha }_i{\mathbf{x}}_i:m\ge 1,\forall i\in [m],{\mathbf{x}}_i\in \mathcal{X},{\alpha }_i>0,\sum _{i=1}^m{\alpha }_i=1\}.$$

让$\text{Epi}f$表示$f:\mathcal{X}\to \mathbb{R}$的epigraph ，也就是一系列的点在函数图像的上面：$\{(x,y):x\in \mathcal{X},y\ge f(x)\}$。

定义2.7：凸函数（Convex function） 令$\mathcal{X}$表示凸集。函数$f:\mathcal{X}\to \mathbb{R}$是凸集当且仅当$\text{Epi}f$是凸集，或者对所有$\mathbf{x},\mathbf{y}\in \mathcal{X}$和$\alpha \in [0,1]$，

$$f(\alpha \mathbf{x}+(1-\alpha \mathbf{y}))\le \alpha f(\mathbf{x})+(1-\alpha )f(\mathbf{y}).$$

当上式$\mathbf{x}\ne \mathbf{y}$时，$f$是严格凸函数。$f$是（严格）凹函数当$-f$是（严格）凸函数。下图是一个简单的凸凹函数的例子。凸函数也可以用它们的一阶或二阶微分来表示。

上图：（左）凸和（右）凹函数的例子。注意，在凸函数上两点之间绘制的任何线段都位于函数图形的上方，而在凹函数上两点之间绘制的任何线段都位于函数图形的下方。

定理2.8： 令$f$是可微函数，$f$是凸的当且仅当$\text{dom}(f)$是凸的，并且下述不等式成立：

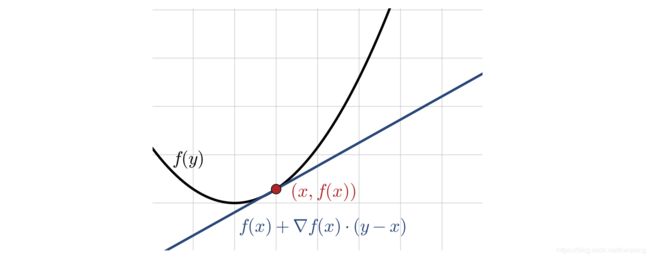
$$\forall \mathbf{x},\mathbf{y}\in \text{dom}(f),f(\mathbf{y})-f(\mathbf{x})\ge \nabla f(\mathbf{x})\cdot (\mathbf{y}-\mathbf{x}).$$

下图展示了上述不等式的性质：对于一个凸函数，超平面在$\mathbf{x}$处的切线总是在函数图像的下方。

定理2.9： 令$f$为二次可微函数，$f$是凸的当且仅当$\text{dom}f$是凸的并且它的海森矩阵是正半定的：

$$\forall \mathbf{x}\in \text{dom}(f),{\nabla }^{2}f(\mathbf{x})\ge 0.$$

如果一个对称矩阵的所有特征值都是非负的，那么它就是半正定的。那么当$f$是标量时，这个定理表明$f$是凸的当且仅当它的二阶导数总是非负的，即对于所有$x\in \text{dom}(f),f^{\prime \prime }(x)\ge 0$。

例子2.10： 线性函数（Linear functions）任何线性函数$f$既是凸又是凹的，因为根据线性方程的定义，定义2.7对于$f$和$-f$都成立。

例子2.11： 二次函数（Quadratic functions） 函数$f:x\mapsto x^2$是定义在$\mathbb{R}$上的凸函数，因为它是二次可微的并且对于所有$x\in \mathbb{R}$，$f^{\prime \prime }(x)=2>0$。

例子2.12：范数（Norms） 由范数的齐次性和三角不等式性，定义在凸集$\mathcal{X}$上的任意范数$||\cdot ||$是凸的。对所有的$\alpha \in [0,1],\mathbf{x},\mathbf{y}\in \mathcal{X}$，我门可以写成

$$||\alpha \mathbf{x}+(1-\alpha )\mathbf{y}||\le ||\alpha \mathbf{x}||+||(1-\alpha )\mathbf{y}||=\alpha ||\mathbf{x}||+(1-\alpha )||\mathbf{y}||.$$

定理2.13：琴生不等式（Jensen’s inequality） 令$\mathbf{X}$是来自取值为一个非空凸集$\mathcal{C}\subseteq {\mathbb{R}}^N$并且其有限期望是$\mathbb{E}[\mathbf{X}]$的随机变量并且$f$是定义在$\mathcal{C}$上的可测凸函数。则$\mathbb{E}[\mathbf{X}]$属于凸集$\mathcal{C}$并且$\mathbb{E}[\mathbf{X}]$是有限的，则下述不等式成立：

$$f(\mathbb{E}[\mathbf{X}])\le \mathbb{E}[f(\mathbf{X})].$$

2.3 约束最优化（Constrained optimization）

  我们现在定义一个一般的约束优化问题和凸约束优化问题的具体性质。

定义2.14：约束最优化问题（Constrained optimization problem） 令$\mathcal{X}\subseteq {\mathbb{R}}^N$并对所有的$i\in [m]$，$f,g_i:\mathcal{X}\to \mathbb{R}$。则约束最优化问题是如下形式：

$$\begin{gathered} \underset{\mathbf{x}\in \mathcal{X}}{\min }f(\mathbf{x}) \\ \text{subjext to}:g_i(\mathbf{x})\le 0,\forall i\in \{1,\cdots ,m\}. \end{gathered}$$

这个一般公式不做任何凸性假设，并且可以用等式约束加以扩充。与稍后介绍的相关问题相比，它被称为原始问题（primal problem）。我们将用$p^{\ast }$来表示目标函数的最佳值。

  对于任何$\mathbf{x}\in \mathcal{X}$，我们将用$g(\mathbf{x})$表示向量$(g_1(\mathbf{x}),\cdots ,g_m(\mathbf{x}){)}^{\top }$。因此，约束可以写成$g(\mathbf{x})\le 0$。对于任何约束优化问题，我们可以把在分析问题或与另一个相关的优化问题中起重要作用的拉格朗日函数（Lagrange function）联系起来。

定义2.15：拉格朗日（Lagrangian） 与一般约束最优化问题相关的拉格朗日函数在$\mathcal{X}\in {\mathbb{R}}_{+}$的定义如下：

$$\forall x\in \mathcal{X},\forall \alpha \ge 0,\mathcal{L}(\mathbf{x},\alpha )=f(\mathbf{x})+\sum _{i=1}^m{\alpha }_i{g}_i(\mathbf{x}).$$

注意，对于凸优化问题，等式约束函数$g(\mathbf{x})$必须是仿射函数，因为无论是$g(\mathbf{x})$和$-g(\mathbf{x})$都需要是凸的。

定义2.16：对偶函数（Dual function） 与约束优化问题相关的（拉格朗日）对偶函数定义如下：

$$\forall \alpha >0,F(\alpha )=\underset{\mathbf{x}\in \mathcal{X}}{\inf }\mathcal{L}(\mathbf{x},\alpha )=\underset{\mathbf{x}\in \mathcal{X}}{\inf }(f(\mathbf{x})+\sum _{i=1}^m{\alpha }_i{g}_i(\mathbf{x})).$$

注意$F$经常是凹函数，因为关于$\alpha$的拉格朗日函数是线性的，因为下确界保留凹性。我们进一步观察到

$$\forall \alpha \ge 0,F(\alpha )\le p^{\ast },$$

因为对于任何的$\mathbf{x}$，$f(\mathbf{x})+{\sum }_{i=1}^m{\alpha }_i{g}_i(\mathbf{x})\le f(\mathbf{x})$。对偶函数自然会导致下述优化问题。

定义2.17：对偶问题（Dual problem） 与对偶（优化）问题相关联的约束优化问题是

$$\begin{gathered} \underset{\alpha }{\max }F(\alpha ) \\ \text{subject to}:\alpha \ge 0. \end{gathered}$$

对偶问题总是凸优化问题（最大化凹问题）。令$d^{\ast }$表示最优解，下述不等式成立：

$$d^{\ast }\le p^{\ast }.$$

上式是弱对偶问题。它们的差值是$p^{\ast }-d^{\ast }$，也被称作是对偶差（duality gap）。上式取等时，称为强对偶问题。

  如果需要深入研究凸优化等问题，推荐Stephen boyd的《凸优化》，下篇更新《机器学习中的数学（中）》，to be continued…