深度学习DeepLearning.ai系列课程学习总结：13. 超参数调优、Batch正则化理论及深度学习框架学习

转载过程中，图片丢失，代码显示错乱。

为了更好的学习内容，请访问原创版本：

https://www.missshi.cn/api/view/blog/5a2273939112b35ff3000002

Ps：初次访问由于js文件较大，请耐心等候（5s左右）

 

 

在本文中，我们将了解一些机器学习中的超参数调优、Batch正则化及深度学习框架。

主要包括：

1. 超参数调试经验

2. 深层神经网络中隐藏层的归一化

3. Batch正则化

4. Softmax分类回归问题

5. 深度学习框架简介

超参数调试经验

在之前的学习中，我们已经了解到神经网路的涉及过程中，我们选择设置大量的超参数。 
那么如果选择、调试这些超参数呢？接下来的内容将有助于你掌握这些技巧。 
超参数有哪些呢？

• α α ：学习速率
• β β ：momentum梯度下降法
• β1,β2,ϵ β1,β2,ϵ ：Adam优化算法
• 网络层数
• 每层中神经元数量
• decay_rate decay_rate ：学习速率衰减速度
• Mini-batch size

其中，最需要调试的可能就是学习速率 α α啦！ 
此时，可能是 β β，Mini-batch size以及每层中神经元数量。 
再然后，我们可以调试网络层数和 decay_rate decay_rate。 
对于 β1,β2,ϵ β1,β2,ϵ而言，我们通常可以设置默认值： 

β1=0.9,β2=0.999,ϵ=10−8 β1=0.9,β2=0.999,ϵ=10−8

那么具体而言，我们应该如何进行参数调试呢？ 
在早期的机器学习中，我们调试的方式通常如下： 
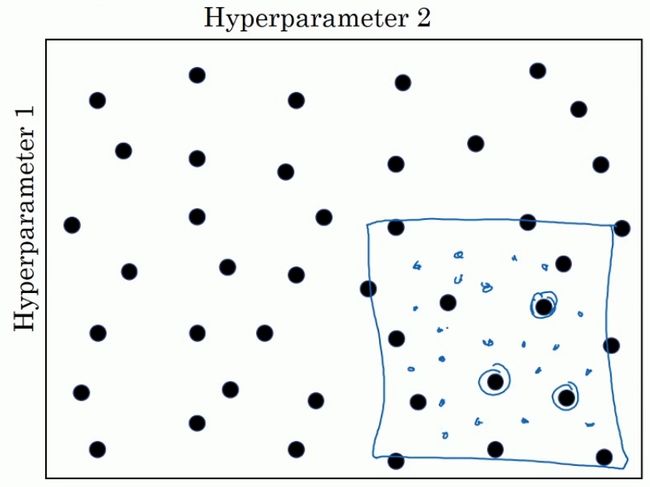
假设有两个超参数：参数1和参数2。 
我们可以将两个点构成一个平面，并在平面上均匀选择一系列点，并找出其中的最优点。 
 
这一个方法在参数较少的时候比较实用。 
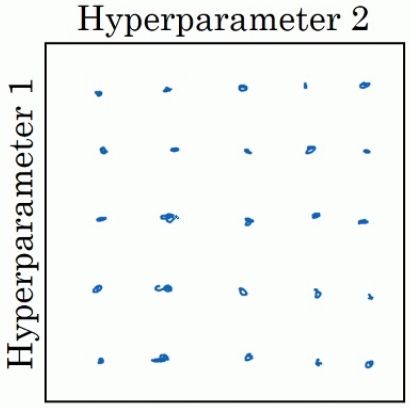
而对于深度学习的应用而言，我们推荐的方法如下： 
同样是在平面上选择一系列点，不过不再是均匀选择，而是随机选择： 
 
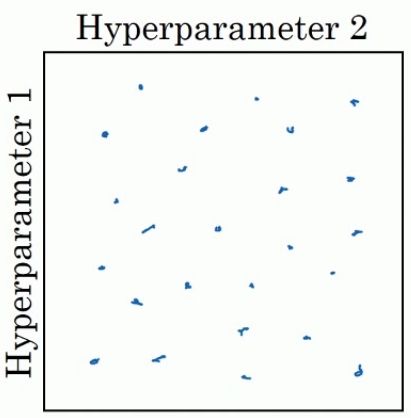
为什么这么做呢？最大的原因是因为在深度学习应用中，我们有时无法确定哪些超参数的影响更大，通过随机选择点，可以达到在每个维度上有更多的值进行选择，从而得到相对更好的结果。

此外，在深度学习应用中，另外一个常用的参数调试方法为从粗粒度到细粒度：

1. 首先对在整个空间中随机选择一系列点，并找出其中的相对较优点集中的区域。
2. 将该区域进行方法，并在该区域中中随机选择一系列点，并找出其中的相对较优点集中的区域。

当然，在有些场合中，直接使用随机选点有时并不合适。 
以调试超参数学习速率为例，假设 α=0.0001,...,1 α=0.0001,...,1。 
此时，如果随机选点的话，大约将会有90%的点落在0.1到1之间，而只有10%的点在0.0001到0.1之间，很明显这并不合理。 
此时，更合理的一种方式是使用对数标尺后再进行随机选择。 

即代码实现如下：

   
   
   
   

    
    
    
    
r = -4 * np.random.rand()
    
    
    
    
alpha = 10 ** r
   
   
   
   

下面，我们再来讨论一下用于指数加权平均中的参数 β β。 
通常我们认为 β β的取值范围应该是在0.9到0.999之间。 
那么我们应该如何进行随机选点呢？ 
此时， 1−β 1−β的取值范围应该是在0.0001到0.1之间。 
从而随机选点的代码实现如下：

   
   
   
   

    
    
    
    
r = -2 * np.random.rand() - 1 # [-3, -1]
    
    
    
    
beta = 1 - 10 ** r
   
   
   
   

最后，在补充一些关于深度学习中参数训练的一些Tips：

• 随着数据集或样本等的变化，之前已经调整好的参数可能会在一段时间后不再适用，因此每隔几个月建议重新调整/测试一下参数。
• 参数训练的两种方式：Babysitting适用于有足够大的数据但是没有充足的计算资源的情况下，每次训练一个模型，并在训练的过程中不断观察结果并随时进行参数调整。另一种方法则是在有充足的计算资源的情况下，我们可以同时训练某模型在不同的参数情况下的效果。然后从中选择合适的超参数对应的模型。

深层神经网络中隐藏层的归一化

在利用数据进行训练之前，我们通常需要对数据进行归一化。 
正则化的优点是可以加快我们的训练过程从而使得更快的寻找到最优值。 
在之前的学习中，我们都讲述了对输入的数据进行正则化，例如下图中的 x1,x2,x3 x1,x2,x3。 
 
然而，对于一个多层的神经网络而言，我们在计算 w[3],b[3] w[3],b[3]时，同样希望其中间层 a[2] a[2]进行归一化，这样将有助于整体训练过程的优化： 
 
Ps：补充说明一下，在实际过程中，我们通常是对 z[l] z[l]进行归一化。

那么如何对 z[l] z[l]进行归一化呢？ 
前面的步骤与输入变量的归一化一致，假设 z[l] z[l]包含为元素为 z(1),...,z(m) z(1),...,z(m)。 

μ=1m∑iz(i)σ2=frac1m∑i(zi−μ)2z(i)norm=z(i)−μσ2+ε−−−−−√ μ=1m∑iz(i)σ2=frac1m∑i(zi−μ)2znorm(i)=z(i)−μσ2+ε

此时，我们已经将 z z转化为了均值为0，方差为1的向量了。 
但是，为了更好的进行优化，我们期望可以对其添加合适的均值和方差： 

z˜(i)=γz(i)norm+β z~(i)=γznorm(i)+β

其中， γ γ和 β β是我们要调试的超参数。通过选择合适的参数，可以用于控制其均值和方差。

Batch归一化

我们已经了解了如何在深层神经网络中对隐藏层进行归一化了，那么我们来在真实神经网络中看一下吧： 

对于上图中的每个神经元而言，其主要完成两个工作，第一个是计算 z z，另外就是计算 a a。 
 
在使用Batch归一化时，计算流程图简要如下： 

通过输入x得到z之后，先进行Batch归一化后再去计算a。 
此时，我们在每一层中需要训练的参数除了 w w， b b，还新增了 β β， γ γ。 
接下来，我们可以使用之前学到的任意一种优化算法来进行反向传播计算。 
Ps：在实践中，Batch归一化方法通常会与mini-batches结合使用。

那么，Batch归一化为什么会那么有效呢？ 
之前，我们已经了解到对输入数据进行归一化可以有效的提升训练速度，原因在于我们将模型的最优值范围变得更加规则。那么从直观上理解的话，Batch归一化也是起到了相同的效果。 
那么更深层次的原因呢？

1. Batch归一化可以是深层网络的鲁棒性更强：在每个隐藏层进行归一化有助于削弱之前层的一些特殊值变化带来的影响，从而保证整个神经网络有着更强的鲁棒性。
2. Batch归一化一定程度上起到正则的效果：由于Batch归一化常常与mini-batches方法结合，因此每次迭代只是由其中一部分数据得到的，存在一定程度的波动。通过添加一定程度的噪声（均值和方差的调整），可以起到与Dropout（随机禁用某些神经元）类似的效果。

在上述的讨论中，我们始终围绕着mini-batches方法来学习Batch归一化的基本理论和实践，而在应用或测试的过程中，每次传入的值可能是一个样本，而不是一个mini-batch。因此，我们需要在继续了解如何在测试中应用。 
回忆一下，训练过程如下： 

μ=1m∑iz(i)σ2=frac1m∑i(zi−μ)2z(i)norm=z(i)−μσ2+ε−−−−−√z˜(i)=γz(i)norm+β μ=1m∑iz(i)σ2=frac1m∑i(zi−μ)2znorm(i)=z(i)−μσ2+εz~(i)=γznorm(i)+β

而在测试时，如果我们每次输入只有一个样本时，计算均值和方差是没有意义的。 
为了将网络应用于测试，我们需要使用指数加权平均法来估计均值和方差：具体做法就是根据训练集中的数据来估算整个样本集的均值和方差，然后在测试过程中，直接使用训练样本集估算得到的均值和方差。

Softmax分类回归问题

在之前的学习中，我们主要都是在讨论二分类问题。 
那么，对于多分类问题应该怎么解决呢？Softmax是解决多分类问题的常见方法。 
假设我们现在需要创建一个网络用于识别猫、狗和小鸡： 

对于猫，我们希望输出1。狗输出2。小鸡输出3。其他则输出0。 
我们使用 C C表示分类的类别数。此时 C=4 C=4。 
如果用一个简化的神经网络来表示可以入下图所示： 

其输出层的神经元数目应该与 C C相等。 
此时，我们希望输出层每个神经元的值表示该输入对应于该分类的概率是多少，从而我们来判断其更有可能属于哪个分类。 
此外，我们希望最后一层 C C个神经元输出值之和为1。 
为了满足这些条件，我们将会用到刚才提到的Softmax层来生成输出： 
以第 L L层进行说明，计算 z[L] z[L]的方式并没有发生变化： 

z[L]=w[L]a[L−1]+b[L] z[L]=w[L]a[L−1]+b[L]

然而，此时激活函数则要进行一些调整： 

t=ez[L]a[L]=ez[L]∑Cj=1ti t=ez[L]a[L]=ez[L]∑j=1Cti

可能仅仅看公式有些抽象，下面我们将用一个具体的例子来进行讲解： 
假设： 

z[L]=[5,2,−1,3] z[L]=[5,2,−1,3]

则 

t=[e5,e2,e−1,e3]=[148.4,7.4,0.4,20.1]∑j=14ti=148.4+7.4+0.4+20.1=176.3a[L]=[148.4/176.3,7.4/176.3,0.4/176.3,20.1/176.3]=[0.842,0.042,0.002,0.114] t=[e5,e2,e−1,e3]=[148.4,7.4,0.4,20.1]∑j=14ti=148.4+7.4+0.4+20.1=176.3a[L]=[148.4/176.3,7.4/176.3,0.4/176.3,20.1/176.3]=[0.842,0.042,0.002,0.114]

此时，就分类而言，输出的结果将会是四个神经元中最大的数对应的分类，此处即为0.842对应的分类0。 
下列一系列图都是多分类问题的常见场景： 

那么Softmax网络该如何进行训练呢？ 
首先我们需要定义一下损失函数： 

L(yˆ,y)=−∑j=1Cyjlogyˆj L(y^,y)=−∑j=1Cyjlogy^j

假设y=[0, 1, 0, 0]，而 yˆ y^=[0.3, 0.2, 0.1, 0.4]，则： 

L(yˆ,y)=−y2logyˆ2 L(y^,y)=−y2logy^2

此时，如果希望L尽可能小的方式就是是的 y2 y2尽可能的大。 
那么，对于一个batch来说，代价函数J应该怎么计算呢？ 

J(w,b)=1m∑i=1mL(yˆ(i),y(i)) J(w,b)=1m∑i=1mL(y^(i),y(i))

深度学习框架简介

随着神经网络变得越来越复杂，每次自己从零开始构建网络已经变得成本越来越高。 
幸运的是，目前有很多强大的神经网络框架可以供我们直接调用。 
利用这些框架，我们将不再需要纠结于如何实现网络计算，如何进行反向传播，从而可以把更多的精力用于模型结构的设计与调优上。 
目前，流程的深度学习框架有很多，如下图所示： 
 
每个框架都有其特点和适用的场景。同时，这些框架也在不断的改进和维护。 
那么，该如何选择框架呢？

• 易用，易编程
• 计算效率高
• 是否会长时间开源
• 支持的语言

根据这几个特点，大家可以选择自己感兴趣的框架进行学习。不过在本系列文章的后续内容中，我们主要将会基于Tensorflow来进行实践。

 

更多更详细的内容，请访问原创网站：

https://www.missshi.cn/api/view/blog/5a2273939112b35ff3000002

Ps：初次访问由于js文件较大，请耐心等候（5s左右）