scikit-learn 朴素贝叶斯类库

scikit-learn 朴素贝叶斯类库

朴素贝叶斯方法是基于贝叶斯定理的一组有监督学习算法，即“简单”地假设每对特征之间相互独立。 给定一个类别 $y$ 和一个从$ x_1$ 到 $x_n$的相关的特征向量， 贝叶斯定理阐述了以下关系:
$$P(y|x_1，x_2，\dots ，x_n)=\frac{P(y)P(x_1，\dots ，x_n|y)}{P(x_1，\dots ，x_n)}$$
使用简单(navie)的假设-每对特征之间都是相互独立的：
$$P(x_i|y，x_1，x_2，\dots ，x_{i-1}，x_{i+1}，\dots ，x_n)=P(x_i|y)$$
可以对关系式进行化简为：
$$P(y|x_1，\dots ，x_n)=\frac{P(y){\prod }_{i=1}^{n}P(x_i|y)}{P(x_1，\dots ，x_n)}$$
由于在给定的输入中$P(x_1，\dots ，x_n)$是常量，使用下面的分类规则：
$$P(y|x_1，\dots ，x_n)\propto P(y)\prod _{i=1}^{n}P(x_i|y)$$
$$\hat{y}=arg\underset{y}{max}P(y)\prod _{i=1}^{n}P(x_i|y)$$
我们可以使用最大后验概率(Maximum A Posteriori, MAP) 来估计 $P(y)$和$P(x_i|y)$，前者是训练集中类别 $y$的相对频率。各种各样的的朴素贝叶斯分类器的差异大部分来自于处理$P(x_i\mid y)$分布时的所做的假设不同。
尽管其假设过于简单，在很多实际情况下，朴素贝叶斯工作得很好，特别是文档分类和垃圾邮件过滤。这些工作都要求 一个小的训练集来估计必需参数。相比于其他更复杂的方法，朴素贝叶斯学习器和分类器非常快。 分类条件分布的解耦意味着可以独立单独地把每个特征视为一维分布来估计。这样反过来有助于缓解维度灾难带来的问题。
另一方面，尽管朴素贝叶斯被认为是一种相当不错的分类器，但却不是好的估计器(estimator)，所以不能太过于重视从predict_proba输出的概率。

---

1.高斯朴素贝叶斯

GaussianNB实现了运用于分类的高斯朴素贝叶斯算法。特征的可能性(即概率)假设为高斯分布:
$$P(x_i\mid y)=\frac{1}{\sqrt{2\pi {\sigma }_y^2}}exp⟮-\frac{(x_i-{\mu }_y{)}^2}{2{\sigma }_y^2}⟯$$
参数${\sigma }_y$和${\mu }_y$使用极大似然然估计。

---

2. 多项分布朴素贝叶斯

MultinomialNB实现了服从多项分布数据的朴素贝叶斯算法，也是用于文本分类(这个领域中数据往往以词向量表示，尽管在实践中 tf-idf 向量在预测时表现良好)的两大经典朴素贝叶斯算法之一。布参数由每类 $y$ 的 ${\theta }_y=({\theta }_{y1},\dots ,{\theta }_{yn})$向量决定， 式中 $n$ 是特征的数量(对于文本分类，是词汇量的大小)${\theta }_{yi}$ 是样本中属于类 $y$ 中特征$i$ 概率$P(x_i\mid y)$。
参数 ${\theta }_y$ 使用平滑过的最大似然估计法来估计，即相对频率计数:
$${\hat{\theta }}_{yi}=\frac{N_{yi}+\alpha }{N_y+\alpha n}$$
式中 $N_{yi}={\sum }_{x\in T}{x}_i$ 是 训练集 $T$ 中 特征 $i$在类 $y$ 中出现的次数，$N_y={\sum }_{i=1}^{|T|}{N}_{yi}$ 是类 $y$ 中出现所有特征的计数总和。
先验平滑因子 $\alpha \ge 0$ 应用于在学习样本中没有出现的特征，以防在将来的计算中出现0概率输出。 把 $\alpha =1$ 被称为拉普拉斯平滑(Lapalce smoothing)，而 $\alpha <1$ 被称为利德斯通平滑(Lidstone smoothing)。

---

3. 伯努利朴素贝叶斯

BernoulliNB实现了用于多重伯努利分布数据的朴素贝叶斯训练和分类算法，即有多个特征，但每个特征 都假设是一个二元 (Bernoulli, boolean) 变量。 因此，这类算法要求样本以二元值特征向量表示；如果样本含有其他类型的数据， 一个BernoulliNB实例会将其二值化(取决于binarize参数)。
伯努利朴素贝叶斯的决策规则基于
$$P(x_i\mid y)=P(i\mid y)x_i+(1-P(i\mid y))(1-x_i)$$
与多项分布朴素贝叶斯的规则不同 伯努利朴素贝叶斯明确地惩罚类$y$中没有出现作为预测因子的特征$i$ ，而多项分布分布朴素贝叶斯只是简单地忽略没出现的特征。
BernoulliNB一共有4个参数，其中3个参数的名字和意义和MultinomialNB完全相同。唯一增加的一个参数是binarize。这个参数主要是用来帮BernoulliNB处理二项分布的，可以是数值或者不输入。如果不输入，则BernoulliNB认为每个数据特征都已经是二元的。否则的话，小于binarize的会归为一类，大于binarize的会归为另外一类。
在文本分类的例子中，词频向量(word occurrence vectors)(而非词数向量(word count vectors))可能用于训练和用于这个分类器。 BernoulliNB可能在一些数据集上可能表现得更好，特别是那些更短的文档。实际使用时，最好对两个模型都进行评估。

---

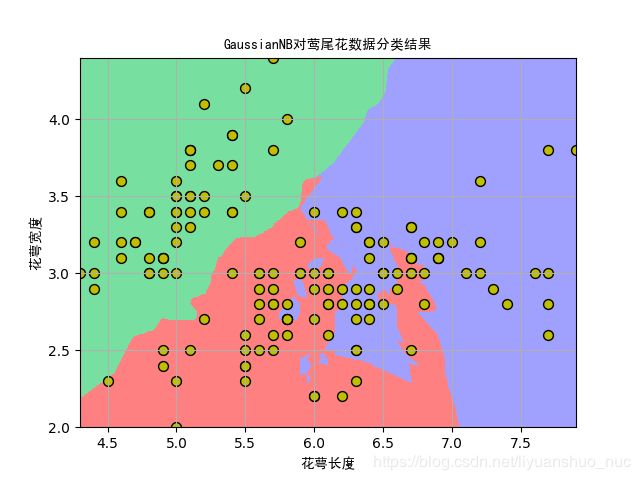
4. 在莺尾花数据集上的测试代码及结果

import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
from sklearn.preprocessing import StandardScaler
from sklearn.naive_bayes import GaussianNB, MultinomialNB
from sklearn.pipeline import Pipeline
from sklearn.neighbors import KNeighborsClassifier

#解决中文显示乱码的问题
from matplotlib.font_manager import FontProperties
myfont = FontProperties(fname='/home/liyuanshuo/Downloads/simheittf/simhei.ttf')


def iris_type(s):
    it = {b'Iris-setosa': 0, b'Iris-versicolor': 1, b'Iris-virginica': 2}
    return it[s]

def GasssianNB_test():
    data = np.loadtxt('iris.data', dtype=float, delimiter=',', converters={4: iris_type})
    print(data)
    x, y = np.split(data, (4, ), axis=1)
    x = x[:, :2]
    print(x)
    print(y)

    gnb = Pipeline([('sc', StandardScaler()), ('clf', GaussianNB())])
    gnb.fit(x, y.ravel())

    #下面使用多项式分布贝叶斯和K紧邻分类作为对比
    # gnb = MultinomialNB().fit(x, y.ravel())
    # gnb = KNeighborsClassifier(n_neighbors=5).fit(x, y.ravel())

    #下面画图展示结果
    N, M = 500, 500                                     #横纵各采样多少个值
    x1_min, x1_max = x[:, 0].min(), x[:, 0].max()       #第0列的范围
    x2_min, x2_max = x[:, 1].min(), x[:, 1].max()       #第一列的范围
    t1 = np.linspace(x1_min, x1_max, N)
    t2 = np.linspace(x2_min, x2_max, N)
    x1, x2 = np.meshgrid(t1, t2)                        #生成网格采样点
    x_test = np.stack((x1.flat, x2.flat), axis=1)       #测试点


    # mpl.rcParams['font.sans-serif'] = ['simhei']
    mpl.rcParams['axes.unicode_minus'] = False
    # plt.rcParams['font.sans-serif'] = ['simhei']
    plt.rcParams['axes.unicode_minus'] = False
    cm_light = mpl.colors.ListedColormap(['#77E0A0', '#FF8080', '#A0A0FF'])
    cm_dark = mpl.colors.ListedColormap(['g', 'r', 'b'])

    y_hat = gnb.predict(x_test)                         #预测值
    y_hat = y_hat.reshape(x1.shape)                     #保证输入和输出的形状相同
    plt.figure(facecolor='w')
    plt.pcolormesh(x1, x2, y_hat, cmap=cm_light)        #显示预测值
    plt.scatter(x[:, 0], x[:, 1], c='y', edgecolors='k', s=50, cmap=cm_dark)  #显示样本
    plt.xlabel(u'花萼长度', fontsize=14, fontproperties=myfont)
    plt.ylabel(u'花萼宽度', fontsize=14, fontproperties=myfont)
    plt.xlim(x1_min, x1_max)
    plt.ylim(x2_min, x2_max)
    plt.title('GaussianNB对莺尾花数据分类结果', fontsize=18, fontproperties=myfont)
    plt.grid(True)
    plt.show()
    plt.savefig('GaussianNB对莺尾花数据分类结果.png')


    #训练集上的预测结果
    y_hat = gnb.predict(x)
    y = y.reshape(-1)
    result = y_hat==y
    print(y_hat)
    print(result)
    acc = np.mean(result)
    print('训练集分类准确率： %.2f%%'%(100*acc))



if __name__ == '__main__':
    GasssianNB_test()

结果图片如下：

---

5使用随机数据实现的代码

import numpy as np
from sklearn.naive_bayes import GaussianNB, MultinomialNB
from sklearn import metrics


def MultinomialNB_test():
    np.random.seed(0)
    M = 20
    N = 5
    x = np.random.randint(2, size=(M, N))
    x = np.array(list(set([tuple(t) for t in x])))
    M = len(x)
    y = np.arange(M)
    print('样本个数: %d，特征数目: %d'%x.shape)
    print('样本为：\n', x)
    mnb = MultinomialNB(alpha=1)
    mnb.fit(x, y)
    y_hat = mnb.predict(x)
    print('预测类别： ', y_hat)
    print('预测准确率： %.2f%%'%(100*np.mean(y_hat==y)))
    print('系统得分： ', mnb.score(x, y))
    print('系统得分： ', metrics.accuracy_score(y, y_hat))

    err = y_hat != y
    for i, e in enumerate(err):
        if e:
            print(y[i], ': \t', x[i], '被认为与', x[y_hat[i]], '一个类别')


if __name__ == '__main__':
    MultinomialNB_test()s

---