PCL库中Marching Cubes(移动立方体)算法的解析
PCL库中Marching Cubes(移动立方体)算法解析
1. Marching Cubes算法的原理这里不再赘述,不懂的话,提供一下文献资源:
链接:MARCHING CUBES A HIGH RESOLUTION 3D SURFACE CONSTRUCTION ALGORITHM.pdf
提取码:n0wb
或者看这里的讲解:MarchingCubes算法提取等值面的基本原理
2. 提供一下PCL里面的源码,有需要的可以下载:
链接:marchingCubes.zip
提取码:oyw1
打开之后,有四个文件:

marching_cubes文件中实现了marching_cubes类,实现了大部分的Marching Cubes算法,但它是一个抽象类,不可实例化。
marching_cubes_hoppe文件实现了marching_cubes_hoppe类,继承自marching_cubes,实现了marching_cubes中的纯虚函数vexelizeData(),可以实例化。
3. 此篇博文是参考下面博文得出的,希望能讲的更透彻一些
PCL源码剖析之MarchingCubes算法
—————————————————————————————————————————————————————————————
—————————————————————————————————————————————————————————————
下面我们开始正式分析PCL中Marching Cubes的实现方案。
步骤:点云数据体素化->确定顶点与等值面的关系->确定等值面与voxel各个边的交点->根据交点划分三角面。
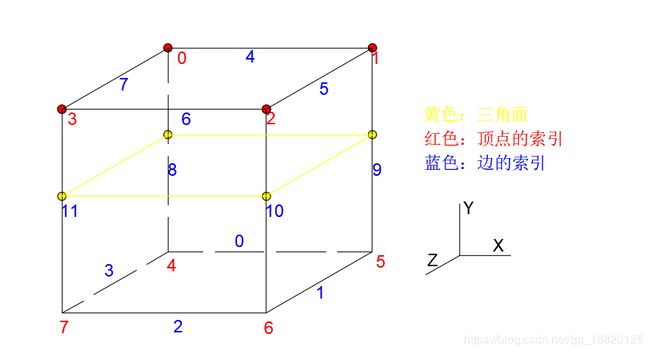
4. 打开marching_cubes.h,找到顶点编号图

这个主要是帮助我们理解算法,8个顶点,12条边,都有各自的编号。更具体的如下图:

5. 打开marching_cubes.hpp,找到performReconstruction()函数。
这里是主函数体,通过调用具体的实现函数,完成了从点云数据到三角面的转换操作。
// 输入参数:无
// 输出参数:1. points:重建得到的三角面,以点序列的形式存储,每三个点代表一个三角面
// 2. polygons:三角面之间的连接关系,对理解算法基本无帮助
template void
pcl::MarchingCubes::performReconstruction (pcl::PointCloud &points,
std::vector &polygons)
{
// iso_level_:等值面的数值,用于判定网格点的两种状态(即在等值面的内外)。
//这里为什么限制取值在(0,1)之间,我也很困惑。不太影响理解,因此略过。
if (!(iso_level_ >= 0 && iso_level_ < 1))
{
PCL_ERROR ("[pcl::%s::performReconstruction] Invalid iso level %f! Please use a number between 0 and 1.\n",
getClassName ().c_str (), iso_level_);
points.width = points.height = 0;
points.points.clear ();
polygons.clear ();
return;
}
// intermediate_cloud:存储三角面的临时点序列
pcl::PointCloud intermediate_cloud;
// res_x_: x方向划分网格的数量
// grid_:存储网格点与等值面的距离,用以和iso_level比较,确定网格点的状态(等值面内外)
grid_ = std::vector (res_x_*res_y_*res_z_, NAN);
// input_:输入的点云数据
// tree_:建立点云数据的KDtree,得到点云内点的关系
tree_->setInputCloud (input_);
// getBoundingBox:计算点云的包围盒,即三个方向的最大最小值,比较简单,不赘述
getBoundingBox ();
// upper_boundary_:包围盒最大值
// lower_boundary_:包围盒最小值
// size_voxel_:体素网格的大小,根据网格的数量和包围盒大小来计算
size_voxel_ = (upper_boundary_ - lower_boundary_)
* Eigen::Array3f (res_x_, res_y_, res_z_).inverse ();
// voxelizeData():将点云数据转化为体素网格的数据,即确定网格点的状态(在等值面的内外)
// 这个函数是纯虚函数,在marching_cubes_hoppe中实现的
voxelizeData ();
// 为三角面的点序列预分配内存。极端情况下,存在6个面的边界Voxel,即2*(YZ+XZ+XY)。假设边界voxel均产生两个三角面,即6个点。
double size_reserve = std::min((double) intermediate_cloud.points.max_size (),
2.0 * 6.0 * (double) (res_y_*res_z_ + res_x_*res_z_ + res_x_*res_y_));
intermediate_cloud.reserve ((size_t) size_reserve);
//对每个Voxel进行三角化操作
for (int x = 1; x < res_x_-1; ++x)
for (int y = 1; y < res_y_-1; ++y)
for (int z = 1; z < res_z_-1; ++z)
{
//index_3d:存储当前voxel的的位置信息xyz
//leaf_node:存储当前voxel中8个顶点(网格点)与等值面的距离
Eigen::Vector3i index_3d (x, y, z);
std::vector leaf_node;
// getNeighborList1D:根据index_3d获得leaf_node的值,即voxel顶点的状态,比较简单,不再赘述
getNeighborList1D (leaf_node, index_3d);
if (!leaf_node.empty ())
// createSurface:根据index_3d和leaf_node得到三角面的点序列intermediate_cloud
createSurface (leaf_node, index_3d, intermediate_cloud);
}
// 将临时点序列intermediate_cloud的内容放到输出点序列points中
points.swap (intermediate_cloud);
// 存储三角面之间的关系,处理简单,用处不大。
polygons.resize (points.size () / 3);
for (size_t i = 0; i < polygons.size (); ++i)
{
pcl::Vertices v;
v.vertices.resize (3);
for (int j = 0; j < 3; ++j)
v.vertices[j] = static_cast (i) * 3 + j;
polygons[i] = v;
}
}
这里我做了比较详细的注释,一般情况下看懂是没问题的。
其中iso_level比较难以理解,如果不明白,可以继续往下看。
6. 打开marching_cubes_hoppe.hpp,找到voxelizeData()函数。
这里完成的是点云体素化,确定顶点与等值面的关系。
template void
pcl::MarchingCubesHoppe::voxelizeData ()
{
//dist_ignore_:限制网格点与点云的最远距离,如果大于此距离,认为网格点与边界过远,不计算。
//is_far_ignored:判定对距离是否有限制。
const bool is_far_ignored = dist_ignore_ > 0.0f;
for (int x = 0; x < res_x_; ++x)
{
const int y_start = x * res_y_ * res_z_;
for (int y = 0; y < res_y_; ++y)
{
const int z_start = y_start + y * res_z_;
for (int z = 0; z < res_z_; ++z)
{
// nn_indices:用于存储当前网格点最近邻点的索引
// nn_sqr_dists:用于存储最近邻点与当前网格点的距离
std::vector nn_indices (1, 0);
std::vector nn_sqr_dists (1, 0.0f);
// point:当前网格点的绝对位置
const Eigen::Vector3f point = (lower_boundary_ + size_voxel_ * Eigen::Array3f (x, y, z)).matrix ();
PointNT p;
p.getVector3fMap () = point;
// 搜索第一个近邻点(由第二个参数决定),即最近邻点,得到其索引和距离
tree_->nearestKSearch (p, 1, nn_indices, nn_sqr_dists);
//如果对最近邻点的距离没有限制或者距离在限制范围内,继续计算
if (!is_far_ignored || nn_sqr_dists[0] < dist_ignore_)
{
// 得到最近邻点的单位法向量
const Eigen::Vector3f normal = input_->points[nn_indices[0]].getNormalVector3fMap ();
// 如果向量存在,进行下一步
if (!std::isnan (normal (0)) && normal.norm () > 0.5f)
//求网格点与等值面的距离,计算方法为最近邻点法向量点乘网格点与最近邻点形成的向量,因为点乘是映射过程
grid_[z_start + z] = normal.dot (
point - input_->points[nn_indices[0]].getVector3fMap ());
}
}
}
}
}

q是网格点,p是最近邻点,grid_[]里面存储的就是q点与 p点所在平面 之间的距离d
7. 打开marching_cubes.hpp,找到createSurface()函数。
这里完成的是 确定等值面与voxel各个边的交点并根据交点划分三角面。
//输入参数:1. leaf_node:存储当前voxel中8个顶点(网格点)与等值面的距离
// 2. index_3d:存储当前voxel的相对位置信息xyz
//输出参数:1. cloud:生成的三角面点序列
template void
pcl::MarchingCubes::createSurface (const std::vector &leaf_node,
const Eigen::Vector3i &index_3d,
pcl::PointCloud &cloud)
{
//cubeindex:存储8个顶点的状态,认为有0000 0000共8位,大于iso_level_的顶点置为0,小于的置为1.(共256种状态)
int cubeindex = 0;
if (leaf_node[0] < iso_level_) cubeindex |= 1;
if (leaf_node[1] < iso_level_) cubeindex |= 2;
if (leaf_node[2] < iso_level_) cubeindex |= 4;
if (leaf_node[3] < iso_level_) cubeindex |= 8;
if (leaf_node[4] < iso_level_) cubeindex |= 16;
if (leaf_node[5] < iso_level_) cubeindex |= 32;
if (leaf_node[6] < iso_level_) cubeindex |= 64;
if (leaf_node[7] < iso_level_) cubeindex |= 128;
// edgeTable:存储边的状态,对应于点的状态,共256种情况,共12位数据,1代表该边被等值面切削,0代表没有。(在marching_cubes.h中)
// cubeindex=255或0时,这时顶点全在等值面一侧,根据表格内容,edgeTable=0,不存在三角面。
if (edgeTable[cubeindex] == 0)
return;
//center:当前体素(接近零点位置的顶点)的绝对位置
const Eigen::Vector3f center = lower_boundary_
+ size_voxel_ * index_3d.cast ().array ();
//p: 存储8个体素顶点的位置
std::vector > p;
p.resize (8);
for (int i = 0; i < 8; ++i)
{
Eigen::Vector3f point = center;
if (i & 0x4)
point[1] = static_cast (center[1] + size_voxel_[1]);
if (i & 0x2)
point[2] = static_cast (center[2] + size_voxel_[2]);
if ((i & 0x1) ^ ((i >> 1) & 0x1))
point[0] = static_cast (center[0] + size_voxel_[0]);
p[i] = point;
}
// 确定体素边与等值面的交点
// vertex_list:存储12个交点的值
std::vector > vertex_list;
vertex_list.resize (12);
//判断如果该边与等值面有交点的话,进行线行插值得到交点
if (edgeTable[cubeindex] & 1)
interpolateEdge (p[0], p[1], leaf_node[0], leaf_node[1], vertex_list[0]);
if (edgeTable[cubeindex] & 2)
interpolateEdge (p[1], p[2], leaf_node[1], leaf_node[2], vertex_list[1]);
if (edgeTable[cubeindex] & 4)
interpolateEdge (p[2], p[3], leaf_node[2], leaf_node[3], vertex_list[2]);
if (edgeTable[cubeindex] & 8)
interpolateEdge (p[3], p[0], leaf_node[3], leaf_node[0], vertex_list[3]);
if (edgeTable[cubeindex] & 16)
interpolateEdge (p[4], p[5], leaf_node[4], leaf_node[5], vertex_list[4]);
if (edgeTable[cubeindex] & 32)
interpolateEdge (p[5], p[6], leaf_node[5], leaf_node[6], vertex_list[5]);
if (edgeTable[cubeindex] & 64)
interpolateEdge (p[6], p[7], leaf_node[6], leaf_node[7], vertex_list[6]);
if (edgeTable[cubeindex] & 128)
interpolateEdge (p[7], p[4], leaf_node[7], leaf_node[4], vertex_list[7]);
if (edgeTable[cubeindex] & 256)
interpolateEdge (p[0], p[4], leaf_node[0], leaf_node[4], vertex_list[8]);
if (edgeTable[cubeindex] & 512)
interpolateEdge (p[1], p[5], leaf_node[1], leaf_node[5], vertex_list[9]);
if (edgeTable[cubeindex] & 1024)
interpolateEdge (p[2], p[6], leaf_node[2], leaf_node[6], vertex_list[10]);
if (edgeTable[cubeindex] & 2048)
interpolateEdge (p[3], p[7], leaf_node[3], leaf_node[7], vertex_list[11]);
// 根据12条边交点的情况生成三角形
//triTable是256*16的数组(在marching_cubes.h中),第一维的256对应256种边界情况,第二维的16对应每种情况下三角形的索引...
//我们知道,一个体素内最多有5个三角面,因此最多需要3*5=15个顶点来存储,这里第16个值均为-1,是为了跳出循环。
for (int i = 0; triTable[cubeindex][i] != -1; i += 3)
{
//根据边界情况得到三角形的交点,存储起来,即完成了整个三角化过程。
PointNT p1, p2, p3;
p1.getVector3fMap () = vertex_list[triTable[cubeindex][i]];
cloud.push_back (p1);
p2.getVector3fMap () = vertex_list[triTable[cubeindex][i+1]];
cloud.push_back (p2);
p3.getVector3fMap () = vertex_list[triTable[cubeindex][i+2]];
cloud.push_back (p3);
}
}
举个栗子:
假如我们的根据leaf_node得出cube_index=15=0000 1111,意味着0,1,2,3端点在等值面内部。我们在edgeTable(在marching_cubes.h中)表中查找第16个数据,edgeTable[15]=0xf00=1111 0000 0000,意味着8,9,10,11四条边与等值面相交,如下:
执行线性插值,即可得到四个交点的具体位置。这里得到了一个空间四边形,下一步需要将其划分为两个三角形,我们就要用到表triTable(在marching_cubes.h中),根据cube_index=15,我们找到triTable[15]={9, 8, 10, 10, 8, 11, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1};取前三个边索引得到 三角形9-8-10,放入三角面点序列;取第4-6个边索引得到 三角形10-8-11,放入点序列;第7个索引边为-1,跳出循环,就完成了三角面的划分。结果如下:
