Spectral(SPY)学习笔记(3)-高光谱降维(Dimensionality Reduction)
实现高光谱数据降维
由于所谓的“维数诅咒”,处理数百个波段的高光谱图像可能会增加计算量,影响分类精度。为了缓解这些问题,通常需要降低数据的维数。
主成分变换
高光谱图像中的许多波段往往具有很强的相关性。主成分变换表示原始图像波段到一组新的、不相关的特征的线性变换。这些新特征对应于图像协方差矩阵的特征向量,其中相关特征值表示特征向量方向上的方差。在相对较少的主成分中(与原始频带数相比)可以捕获到非常大的图像方差百分比。
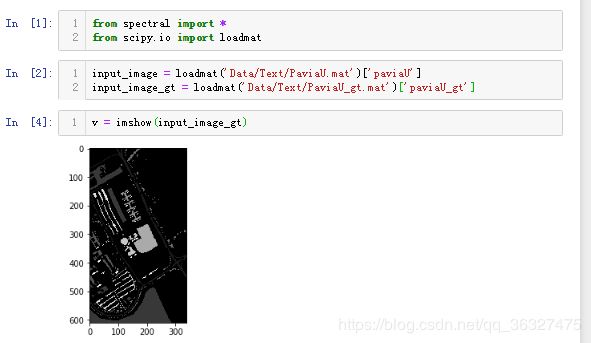
读取数据并显示
 SPy函数principal_components计算图像数据的主组件,并返回一个主组件中的平均值、协方差、特征值和特征向量。该对象还包含一个将数据旋转到主成分空间的变换,以及一个减少特征向量数量的方法。
SPy函数principal_components计算图像数据的主组件,并返回一个主组件中的平均值、协方差、特征值和特征向量。该对象还包含一个将数据旋转到主成分空间的变换,以及一个减少特征向量数量的方法。
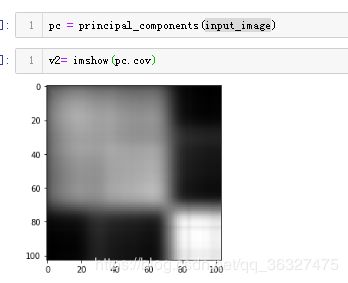
在协方差矩阵显示中,白色表示强正协方差,深色表示强负协方差,灰色表示协方差接近于零。
为了利用主分量降低维数,我们可以按降序对特征值进行排序,然后保留足够的特征值(对应的特征向量),以捕获所需的总图像方差的一部分。然后我们通过将图像像素投影到剩余的特征向量上来降低图像像素的维数。我们将选择保留至少99.9%的总图像方差。
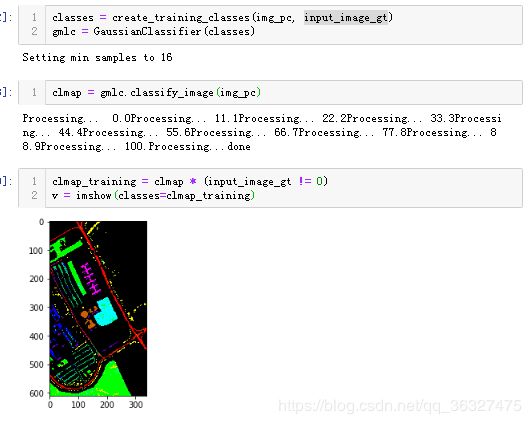
 现在我们将使用高斯最大似然分类器(GMLC)对约简后的主成分进行训练,并根据训练数据进行分类。
现在我们将使用高斯最大似然分类器(GMLC)对约简后的主成分进行训练,并根据训练数据进行分类。